NOIP模拟赛(2019.08.15)

队列变换

一、题目

点此看题
题目：
给定一个0(‘L’)1(‘R’)矩阵，每次对某一行或列取反，问能否达到只有一个元素与其他不同，如果能，输出行列最小的坐标（优先行），如果不能，输出$-1$。
数据范围：
$n\le 1000$

二、解法

我们要求这个最小的答案，从右下角搜到左上角，因为只有0和1，全部变成0和全部变成1是一样的，我们考虑把它全部变0（然后那个为1的就是熊孩子）。
对于最后一行，我们可以使用列操作，就是把它贪心地全部变成0，然后当我们搜上去就不能使用列操作了，因为这样就会打乱下面已经调好的队形，我们在此过程中记录那个较少的值（因为可以使用行取反，只用关注最少的那个值），如果它存在大于1次或有不满足条件的行大于1个，则不可能组成答案，最后判断有没有不满足条件的行。
但有可能答案在最后一行，我们从倒数第二行再做一遍即可。

#include <cstdio>
#include <cstring>
const int MAXN = 1005;
int read()
{
	int x=0,flag=1;char c;
	while((c=getchar())<'0' || c>'9') if(c=='-') flag=-1;
	while(c>='0' && c<='9') x=(x<<3)+(x<<1)+(c^'0'),c=getchar();
	return x*flag;
}
int n,x,y,a[MAXN][MAXN],b[MAXN][MAXN];
int work()
{
	int dif=0;
	for(int i=n;i>=1;i--)
	{
		int cnt0=0,cnt1=0,x0,y0,x1,y1;
		for(int j=n;j>=1;j--)
		{
			if(b[i][j]) cnt1++,x1=i,y1=j;
			else cnt0++,x0=i,y0=j;
		}
		if(cnt0>1 && cnt1>1)
			return 0;
		if(cnt1==1 || cnt0==1)
		{
			dif++;
			if(cnt0==1) x=x0,y=y0;
			else x=x1,y=y1;
		}
		if(dif>1)
			return 0;
	}
	if(dif==0) return 0;
	return 1;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
	{
		char s[MAXN];
		scanf("%s",s+1);
		for(int j=1;j<=n;j++)
			a[i][j]=s[j]=='R';
	}
	memcpy(b,a,sizeof b);
	for(int i=1;i<=n;i++)
		if(b[n][i])
		{
			for(int j=1;j<=n;j++)
				b[j][i]^=1;
		}
	int res=work();
	if(res)
		return !printf("%d %d",x,y);
	memcpy(b,a,sizeof b);
	for(int i=1;i<=n;i++)
		if(b[n-1][i])
		{
			for(int j=1;j<=n;j++)
				b[j][i]^=1;
		}
	res=work();
	if(!res) puts("-1");
	else printf("%d %d",x,y);
}

跨栏

一、题目

点此看题
题目：
给出若干个线段，求删去哪个线段后其他线段互不相交。（保证有解）
数据范围：
$2\le n\le 100000,xi,yi$是小于$1e9$的正整数。

二、解法

前置知识

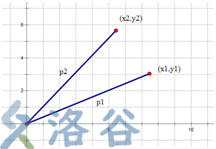
如上图所示：p1和p2是两条线段，它们的一个端点在原点(0,0)，p1的另一个端点在$(x1,y1)$处,p2的另一个端点在$(x2,y2)$处。
线段p1与p2的叉乘为：$p1\times p2=(x1\ast y2)-(x2\ast y1)$
如果叉乘大于0，表示p2在p1的逆时针180度以内，如果小于0，表示p2在p1的顺时针180度以内，如果等于0，表示p1和p2重合。

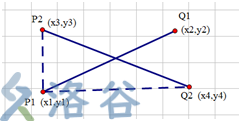
取(x1,y1)和(x3,y3)构成一条虚线，取（x1,y1）和(x4,y4)构成一条虚线，设线段<P1,Q2>与<P1,Q1>的叉乘为m1，线段<P1,Q1>与线段<P1,P2>的叉乘为m2，如果m1*m2>=0,则说明Q2和P2在线段<P1,Q1>的两侧或在线段上面。

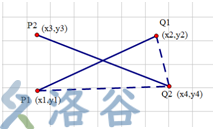
然后再取(x4,y4)和(x1,y1)构成一条虚线，取(x4,y4)和(x2,y2)构成一条虚线，设线段<Q2,P1>与线段<Q2,P2>的叉乘为n1，线段<Q2,P2>与<Q2,Q1>的叉乘为n2，如果n1*n2>=0,则说明P1和Q1分别在线段<P2,Q2>的两侧或在线段上面。
这样就能判断出来线段<P1,Q1>与线段<P2,Q2>是否相交了。

朴素的做法是O(n^2)的。
采用扫描线加set可以做到O(nlogn).
首先，我们需要找出相交的两条线段，那么其中之一就是答案。
如何快速找到相交的两条线段是关键。我们解决这个问题。
将所有点按照x由小到大排序，x相同的按照y由小到大排序。
然后从左到右扫描，如果扫描到的点是一条线段的左端点，则把它加入set，并与set中它的前一条线和后一条线段分别判断一下是否相交；如果扫描到的点是一条线段的右端点，则将它从set中删除，并判断它的前一条线段和后一条线段是否相交。
Set中的线段则按照当前扫描的x坐标对应的y值排序。因为set中的线段一定是跨越当前这个x位置的，如果没有相交，则他们的y坐标的顺序不会发生变化。
这样就找到了两条相交的线段。
然后再判断一下，这两条线段和其他线段相交的次数，就可以知道答案了。
注意有可能爆$longlong$，注意开$double$。

#include <cstdio>
#include <set>
#include <algorithm>
#define eps 1e-8
using namespace std;
const int MAXN = 100005;
int read()
{
	int x=0,flag=1;char c;
	while((c=getchar())<'0' || c>'9') if(c=='-') flag=-1;
	while(c>='0' && c<='9') x=(x<<3)+(x<<1)+(c^'0'),c=getchar();
	return x*flag;
}
int n,a,b;
double nowx;
int sgn(double a)
{  
	return a<-eps?-1:a>eps?1:0;
}
struct point
{
	double x,y;
	point operator - (const point &B)const{return point{x-B.x,y-B.y};}
	double operator *(const point &B)const{return x*B.y-y*B.x;}
}A,B;
struct line
{
	point a,b;
	double k;
	int id;
	bool operator < (const line &B)const {
		double y1=a.y+k*(nowx-a.x),y2=B.a.y+B.k*(nowx-B.a.x);
		if(sgn(y1-y2)) return y1<y2;
		return id<B.id;
	}
}l[MAXN];
set<line> st; 
struct opt
{
	int id,op;
	double x;
	bool operator < (const opt &B)const {
		if(sgn(x-B.x)) return x<B.x;
		return op<B.op;
	}
}q[MAXN*2];
bool pd(const line &u,const line &v)
{
	return ((v.b-v.a)*(u.a-v.a)) * ((v.b-v.a)*(u.b-v.a)) <= 0 && 
		   ((u.b-u.a)*(v.a-u.a)) * ((u.b-u.a)*(v.b-u.a)) <= 0;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
	{
		A.x=read(),A.y=read(),B.x=read(),B.y=read();
		if(A.x>B.x) swap(A,B);
		if(sgn(A.x-B.x))
			l[i].k=(B.y-A.y)/(B.x-A.x);
		else
			l[i].k=0;
		l[i].a=A;l[i].b=B;l[i].id=i;
		q[i*2-1]=opt{i,0,A.x};q[i*2]=opt{i,1,B.x};
	}
	sort(q+1,q+1+n*2);
	for(int i=1;i<=n*2;i++)
	{
		int id=q[i].id;
		nowx=q[i].x;
		if(!q[i].op)
		{
			set<line>::iterator it=st.lower_bound(l[id]);
			if(it!=st.end())
			{
				if(pd(*it,l[id]))
				{
					a=(*it).id,b=id;
					break;
				}
			}
			if(it!=st.begin())
			{
				it--;
				if(pd(*it,l[id]))
				{
					a=(*it).id,b=id;
					break;
				}
			}
			st.insert(l[id]);
		}
		else
		{
			st.erase(l[id]);
			set<line>::iterator it=st.lower_bound(l[id]);
			if(it!=st.begin())
			{
				set<line>::iterator it1=it;
				it1--;
				if(pd(*it1,l[id]))
				{
					a=(*it1).id,b=id;
					break;
				}
			}
			if(it!=st.end())
			{
				if(pd(*it,l[id]))
				{
					a=(*it).id,b=id;
					break;
				}
			}
		}
	}
	int cnt0=0,cnt1=0;
	for(int i=1;i<=n;i++)
	{
		if(i^a && i^b)
		{
			if(pd(l[a],l[i]))cnt0++;
			if(pd(l[b],l[i]))cnt1++;
		}
	}
	if(!cnt0 && !cnt1) printf("%d\n",a<b?a:b);
	if(cnt0>0) printf("%d\n",a);
	else if(cnt1>0) printf("%d\n",b);
}

三角形

一、题目

题目： 点此看题
数据范围：
$1<=n,m<=3000,1<=q<=3000000,1<=A,B,C<=1000000$

二、解法

使用前缀和来维护几个矩形和阶梯矩形，通过作差就可以维护出三角形了。

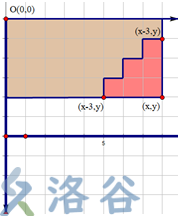
如上图所示，左上角为坐标原点，红色的三角形区域可以由大矩形减去灰色的阶梯矩形求出。
注意这道题要处理阶梯的0位，等于上一层的第一位。

#include <cstdio>
#include <iostream>
#define uint unsigned int 
using namespace std;
const int MAXN = 3005;
int read()
{
	int x=0,flag=1;char c;
	while((c=getchar())<'0' || c>'9') if(c=='-') flag=-1;
	while(c>='0' && c<='9') x=(x<<3)+(x<<1)+(c^'0'),c=getchar();
	return x*flag;
}
int n,m,q;
uint sum[MAXN][MAXN],ans[MAXN][MAXN],a[MAXN][MAXN],res;
uint A,B,C;
uint rng61()
{
    A ^= A << 16;
    A ^= A >> 5;
    A ^= A << 1;
    uint t = A;
    A = B;
    B = C;
    C ^= t ^ A;
    return C;
}
int main(){
    scanf("%d %d %d %u %u %u", &n, &m, &q, &A, &B, &C);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            a[i][j]=rng61();
			sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
			ans[i][j]=ans[i-1][j+1]+sum[i][j]-sum[i-1][j];
		}
		ans[i][0]=ans[i-1][1];
	}
    for(int i=1;i<=q;i++)
	{
        int x=rng61()%n+1;
        int y=rng61()%m+1;
        int k=rng61()%min(x,y)+1;
        res*=233;
        res+=sum[x][y]-ans[x][y-k]+ans[x-k][y]-sum[x-k][y];
    }
    printf("%u\n",res);
}

总结

这次T1用奇形怪状的贪心A了，但T2我不会叉乘，所以我看到T3是三角形有关的内容就直接放弃了，题都没有看完，下一次一定争取把题做完。