7-2 路和回路

---

2024/7/30日补充

思维导图：

 

---

7 - 2 路与回路

定义与基本概念

在图论中，“路”和“回路”是基本且重要的概念。在简单图中，一条路是由一系列结点按顺序连接而成的。具体来说，一条路可以用结点序列来表示。例如，在图 7-2.1 中，有如下定义：

• 路: 由结点序列 𝑣0,𝑣1,𝑣2,…,𝑣𝑛v0​,v1​,v2​,…,vn​ 构成的路径，其中每两个相邻的结点 𝑣𝑖vi​ 和 𝑣𝑖+1vi+1​ 之间有一条边。
• 迹: 由边序列 𝑒1,𝑒2,…,𝑒𝑚e1​,e2​,…,em​ 构成的路径，其中每条边 𝑒𝑖ei​ 是 𝑣𝑖−1vi−1​ 和 𝑣𝑖vi​ 之间的边。
• 通路: 由结点序列 𝑣0,𝑣1,𝑣2,…,𝑣𝑚v0​,v1​,v2​,…,vm​ 构成的路径，其中结点序列中每个结点都不同。
• 圈: 起点和终点相同的路径。

在简单图中，一条路 𝑣0,𝑣1,…,𝑣𝑛v0​,v1​,…,vn​ 可由其结点序列表示。在有向图中，结点数大于1的一条路亦可由边序列 𝑒1,𝑒2,…,𝑒𝑚e1​,e2​,…,em​ 表示。

定理与推论

定理 7-2.1

在一个具有 𝑛n 个结点的简单图中，若一条路有 𝑙l 条边，则结点序列中必有 𝑙+1l+1 个结点。若 𝑙l 大于 𝑛−1n−1，则结点序列中至少有一个结点会重复出现。重复结点及其之间的边可去掉，得到一条边数较少的新路。反复此过程，最终可得到一条从 𝑣0v0​ 到 𝑣𝑛vn​ 的不多于 𝑛−1n−1 条边的路。

推论

在一个具有 𝑛n 个结点的图中，若从结点 𝑣𝑖vi​ 到 𝑣𝑗vj​ 存在一条路，则必存在一条边数小于 𝑛n 的通路。

连通性

定义 7-2.2

在无向图 𝐺G 中，若结点 𝑢u 和 𝑣v 之间存在一条路，则称结点 𝑢u 和结点 𝑣v 是连通的。

不难证明，结点之间的连通性是结点集 𝑉V 上的等价关系。因此，对结点集 𝑉V 作划分，可将 𝑉V 分为若干非空子集 𝑉1,𝑉2,…,𝑉𝑚V1​,V2​,…,Vm​，其中每个子集内的结点彼此连通。这些子图 𝐺(𝑉1),𝐺(𝑉2),…,𝐺(𝑉𝑚)G(V1​),G(V2​),…,G(Vm​) 称为图 𝐺G 的连通分支，记为 𝑤(𝐺)w(G)。

定义 7-2.3

若图 𝐺G 只有一个连通分支，则称 𝐺G 是连通图。在连通图中，任意两个结点之间必是连通的。例如，图 7-2.2 中 (a) 是连通图，而 (b) 是具有三个连通分支的非连通图。

割点与割边

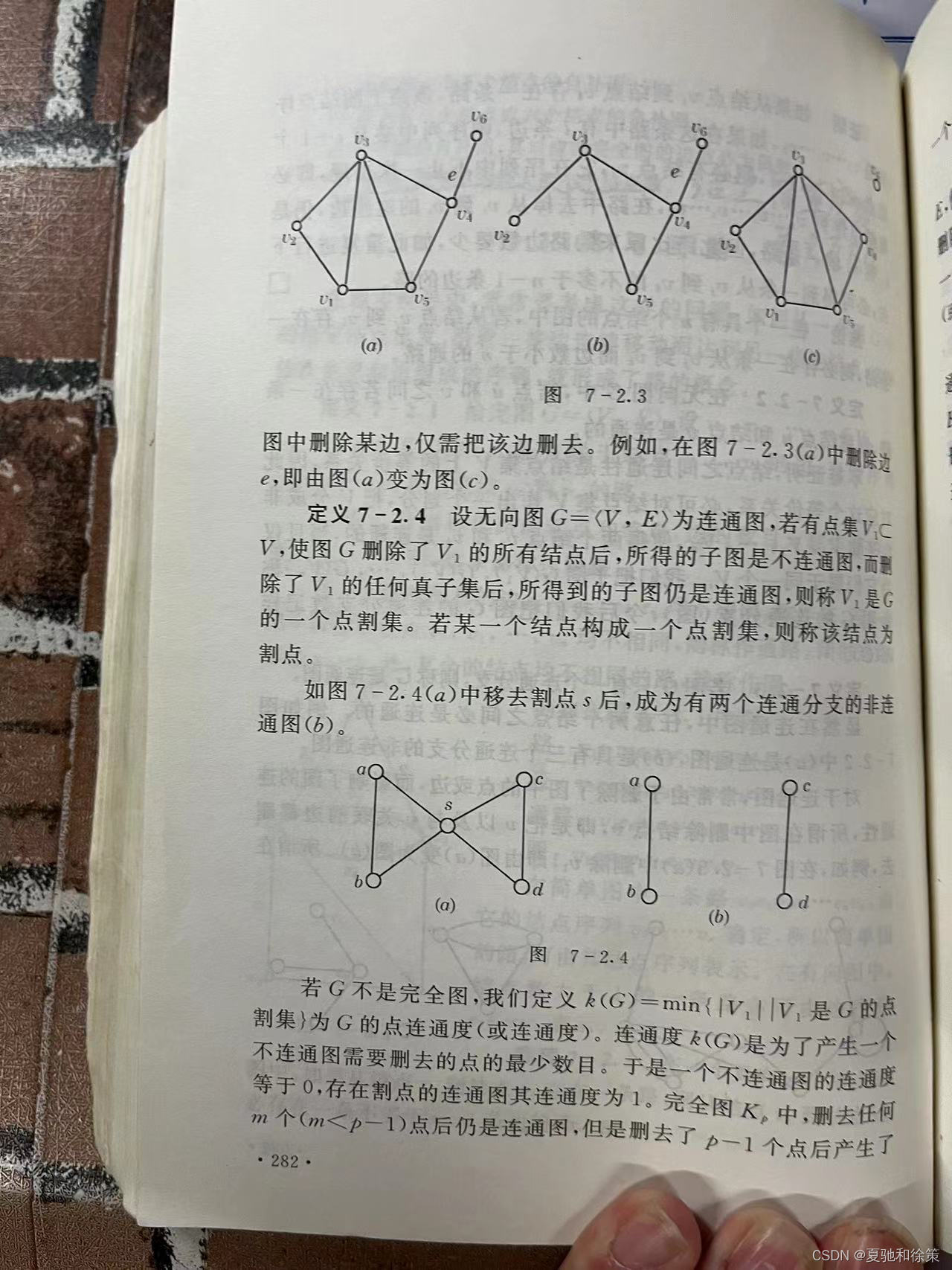
定义 7-2.4

设无向图 𝐺=(𝑉,𝐸)G=(V,E) 为连通图，若有点集 𝑉′⊂𝑉V′⊂V，使得图 𝐺G 删除 𝑉′V′ 的所有结点后所得的子图是不连通图，而删除 𝑉′V′ 的任何真子集后所得的子图仍是连通图，则称 𝑉′V′ 是 𝐺G 的一个点割集。若某一个结点构成一个点割集，则称该结点为割点。

例如，图 7-2.4(a) 中移去割点 𝑠s 后，变为具有两个连通分支的非连通图 (b)。

若 𝐺G 不是完全图，定义 𝑘(𝐺)=min⁡∣𝑉′∣∣𝑉′是G的点割集k(G)=min∣V′∣∣V′是G的点割集 为 𝐺G 的点连通度。连通度 𝑘(𝐺)k(G) 是为了产生一个不连通图需要删去的点的最少数目。

定理 7-2.2

对于任何一个图 𝐺G，有 𝑘(𝐺)≤𝜆(𝐺)≤𝛿(𝐺)k(G)≤λ(G)≤δ(G)。其中，𝜆(𝐺)λ(G) 是边连通度，𝛿(𝐺)δ(G) 是最小度。

有向图的连通性

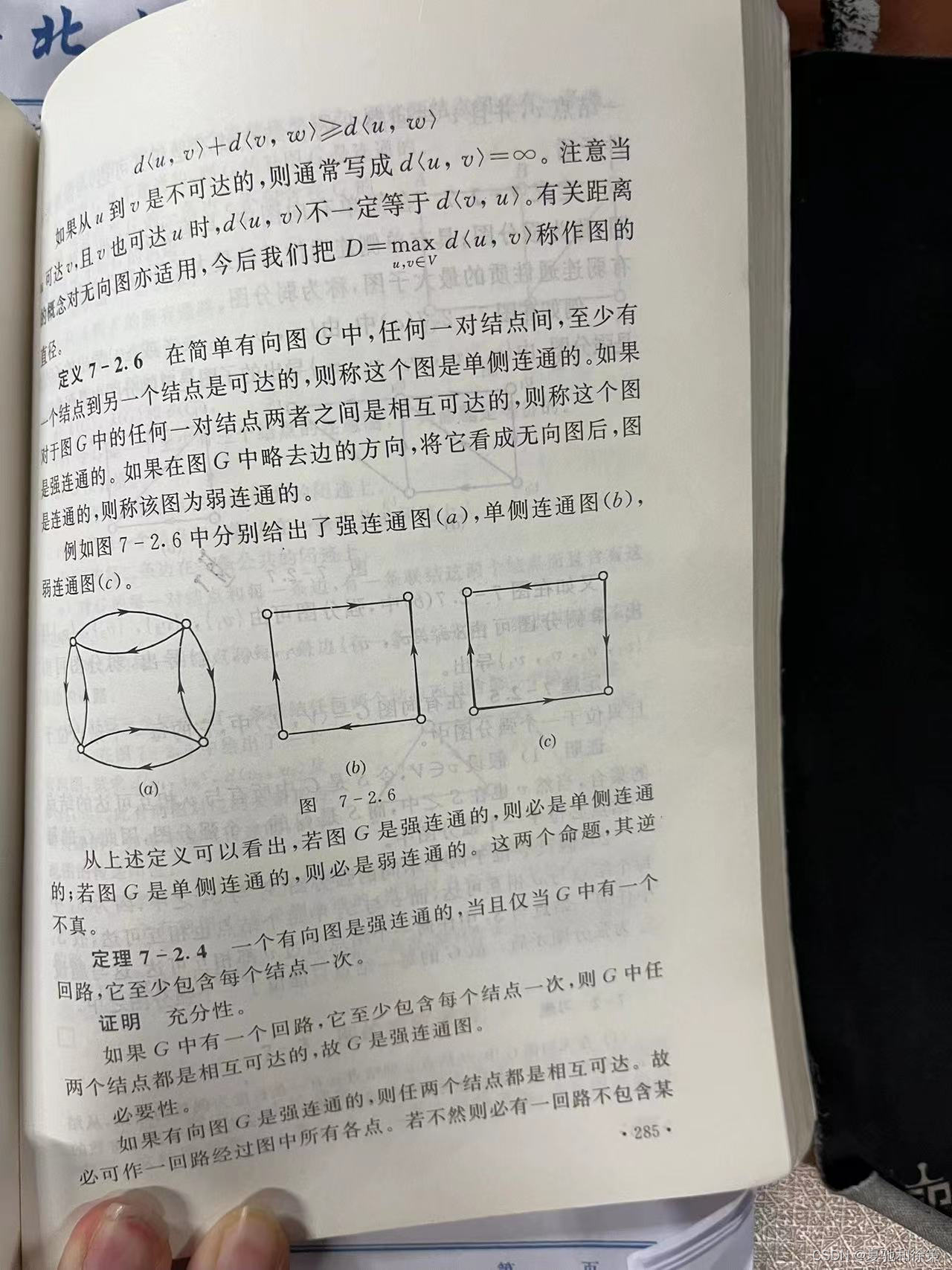
定义 7-2.6

在简单有向图 𝐺G 中，若任何一对结点间至少有一个结点到另一个结点是可达的，则称这个图是单侧连通的。若图 𝐺G 中任何一对结点之间是相互可达的，则称这个图是强连通的。若在图 𝐺G 中略去边的方向后图是连通的，则称该图为弱连通的。

例如，图 7-2.6 中分别给出了强连通图 (a)、单侧连通图 (b) 和弱连通图 (c)。

定理 7-2.5

在有向图 𝐺=(𝑉,𝐸)G=(V,E) 中，每一个结点位于且只位于一个强分图中。

证明：

1. 假设 𝑣∈𝑉v∈V，令 𝑆S 是 𝐺G 中所有与 𝑣v 相互可达的结点的集合，则 𝑆S 是 𝐺G 的一个强分图。因此 𝐺G 的每一结点必位于一个强分图中。
2. 假设 𝑣v 位于两个不同的强分图 𝑆1S1​ 和 𝑆2S2​ 中，则 𝑆1S1​ 中每个结点与 𝑣v 相互可达，𝑣v 与 𝑆2S2​ 中每个结点也相互可达，则 𝑆1S1​ 中任何一结点与 𝑆2S2​ 中任何一结点通过 𝑣v 都相互可达，这与 𝑆1S1​ 为强分图矛盾。因此 𝐺G 的每一结点只能位于一个强分图中。

习题