
思维导图:


第七章 图论
7-1 图的基本概念
我的理解:
理解1:
首先图论始于欧拉当年研究戈尼斯堡七桥问题,这个问题如果给我们来解决我们会如何解决呢,首先遇到的第一个问题就是要把空间中的图形用数学语言表示出来,但是我们和欧拉一样根本就没有数学语言曾经描述过他们,现在我们相当于遇到了个新的问题了,我们该如何表示空间中的一个图形呢?通过观察我们发现图形是空间中一系列点和线的集合组成的因此我们决定用点集和线集来描述空间中的图形
理解2:

图片中看起来不一样的两个图形其实是一个图形这启发我其实看两个图形是否相同不能表面肤浅的看还要看其他方面
理解3:
但此时我们发现我们定义的两个集合该如何把他们用像桥梁一样的东西把他们连接成像图形一样的东西呢?换句话说你随便定义一个点集和边集但是此时他们都是随机散落在这一片空间中的,我们继续观察,通过观察发现呢,每个点如果和边我们给其他点是通过边来联系在一起的,提到联系关系很容易想到离散数学中另一个概念就是序偶,这样呢我们序偶来表示点和边的关系这样无序随机的点集和边集就变得有序了,但此时我们发现不同点在空间的位置不一样我们该如何表示不同点呢很简单我们用符号表示不同点就行了,这个时候有的同学就会问了边怎么办很简单我们不难发现不同的边都是由不同的点表示我们只要把点表示出来就行了
现实世界中许多状态可以用图形来描述。一个图由一些节点和连接两个节点之间的边组成,边的长度和节点的位置是无关紧要的。如图7-1.1(a)和(b)表示了同一个图。
定义7-1.1 图的定义
一个图是一个三元组 𝐺=(𝑉(𝐺),𝐸(𝐺),𝜑)G=(V(G),E(G),φ),其中:
- 𝑉(𝐺)V(G) 是一个非空的节点集合
- 𝐸(𝐺)E(G) 是边集合
- 𝜑φ 是从边集合 𝐸E 到节点的无序偶(或有序偶)集合上的函数
例如,考虑图 𝐺=(𝑉(𝐺),𝐸(𝐺),𝜑)G=(V(G),E(G),φ):
- 𝑉(𝐺)={𝑎,𝑏,𝑐,𝑑}V(G)={a,b,c,d}
- 𝐸(𝐺)={𝑒1,𝑒2,𝑒3,𝑒4,𝑒5,𝑒6}E(G)={e1,e2,e3,e4,e5,e6}
- 边的映射关系为 𝜑(𝑒1)=(𝑎,𝑏)φ(e1)=(a,b), 𝜑(𝑒2)=(𝑎,𝑐)φ(e2)=(a,c), 𝜑(𝑒3)=(𝑏,𝑑)φ(e3)=(b,d), 𝜑(𝑒4)=(𝑏,𝑐)φ(e4)=(b,c), 𝜑(𝑒5)=(𝑑,𝑐)φ(e5)=(d,c), 𝜑(𝑒6)=(𝑎,𝑑)φ(e6)=(a,d)
一个图可以用图形表示,如图7-1.1(a)或(b)。若图中的边 𝑒e 总是与两个节点关联,那么一个图亦可简记为 𝐺=(𝑉,𝐸)G=(V,E),其中 𝑉V 是非空节点集,𝐸E 是连接节点的边集。
若边 𝑒e 与节点无序偶 (𝑣,𝑤)(v,w) 相关联,则称该边为无向边;若边 𝑒e 与节点有序偶 (𝑣,𝑤)(v,w) 相关联,则称该边为有向边。
2024/7/30
我的疑惑:
我在看这个例1的时候遇到了疑惑有序偶和无序偶有什么区别?
解答:其实就是用在不同的图一个用在无向图一个用在有向图其实都是在为了解决不同的问题不同的需求。


度数的定义
在图 𝐺=(𝑉,𝐸)G=(V,E) 中,与节点 𝑣v 相连的边数称为该节点的度数,记作 𝑑𝑒𝑔(𝑣)deg(v)。
例如,在图7-1.3中,节点 𝐴A 的度数为2,节点 𝐵B 的度数为3。每个环在其对应节点上的度数增加2。故图7-1.3中节点 𝐶C 的度数为4。
此外,记 Δ(𝐺)Δ(G) 为图中节点的最大度数,记 𝛿(𝐺)δ(G) 为图中节点的最小度数。如图7-1.4中,Δ(𝐺)=5Δ(G)=5,𝛿(𝐺)=2δ(G)=2。
定理7-1.1
在每个图中,节点度数的总和等于边数的两倍: ∑𝑣∈𝑉𝑑𝑒𝑔(𝑣)=2∣𝐸∣∑v∈Vdeg(v)=2∣E∣
证明:因为每条边连接两个节点,而每条边贡献两个度数,所以节点度数的总和等于边数的两倍。
练习
- 证明:在任何有向完全图中,所有节点入度的平方之和等于所有节点出度的平方之和。
- 写出图7-1.11相对于完全图的补图。
- 证明:图7-1.12中两个图不同构。
- 证明:图7-1.13中两个图是同构的。








图的其他概念
在图的概念中,一个节点的度数可能大于1,但任何一对节点间通常不多于一条边。连接于同一对节点间的多条边称为平行边。
定义7-1.4 多重图
含有平行边的图称为多重图。例如,图7-1.5所示的图均为多重图。在图7-1.5(a)中,节点 𝑎a 和 𝑏b 之间有两条平行边,节点 𝑏b 和 𝑐c 之间有三条平行边,节点 𝑏b 有两个平行的环。
定义7-1.5 简单图和完全图
不含平行边和环的图称为简单图。简单图 𝐺=(𝑉,𝐸)G=(V,E) 中,若每一对节点间都有边相连,则称该图为完全图。有 𝑛n 个节点的无向完全图记作 𝐾𝑛Kn。
定理7-1.4 无向完全图的边数
𝑛n 个节点的无向完全图 𝐾𝑛Kn 的边数为: ∣𝐸∣=𝑛(𝑛−1)2∣E∣=2n(n−1)
证明:在 𝐾𝑛Kn 中,任意两点间都有边相连,𝑛n 个节点中任取两点的组合数为 𝐶(𝑛,2)=𝑛(𝑛−1)2C(n,2)=2n(n−1)。故 𝐾𝑛Kn 的边数为 ∣𝐸∣=𝑛(𝑛−1)2∣E∣=2n(n−1)。
补图的定义
给定任意一个含有 𝑛n 个节点的图 𝐺G,可以通过添加那些没有连接的边,将它补成一个具有相同节点的完全图。补成的图称为 𝐺G 的补图,记作 𝐺′G′。
定义7-1.7 子图和生成子图
设图 𝐺=(𝑉,𝐸)G=(V,E),若图 𝐺′=(𝑉′,𝐸′)G′=(V′,E′) 且 𝑉′⊆𝑉V′⊆V,𝐸′⊆𝐸E′⊆E,则称 𝐺′G′ 是 𝐺G 的子图。若子图包含 𝐺G 的所有节点,则称该子图为 𝐺G 的生成子图。
定义7-1.9 图的同构
设图 𝐺=(𝑉,𝐸)G=(V,E) 及图 𝐺′=(𝑉′,𝐸′)G′=(V′,E′),如果存在一一对应的映射 𝑔:𝑉→𝑉′g:V→V′,且 (𝑣,𝑤)∈𝐸(v,w)∈E 当且仅当 (𝑔(𝑣),𝑔(𝑤))∈𝐸′(g(v),g(w))∈E′,则称 𝐺G 与 𝐺′G′ 同构,记作 𝐺≈𝐺′G≈G′。
同构图的节点和边分别存在一一对应,并保持关联关系。例如图7-1.9中,(a) 与 (b) 是同构的,(c) 与 (d) 也是同构的。
综上所述,可以得到两图同构的一些必要条件:
- 节点数目相同;
- 边数相等;
- 度数相同的节点数目相等。
但以上条件并非充分条件。例如,图7-1.10中(a) 和 (b) 满足上述条件,但它们并不同构。
习题
- 证明:在任何有向完全图中,所有节点入度的平方之和等于所有节点出度的平方之和。
- 写出图7-1.11相对于完全图的补图。
- 证明:图7-1.12中两个图不同构。
- 证明:图7-1.13中两个图是同构的。

图的度数相关概念
定理7-1.2 在任何有向图中,所有结点的入度之和等于所有结点的出度之和
证明:因为每条有向边必对应一个入度和一个出度,若一个结点具有一个入度或出度,则必关联一条有向边。所以,有向图中各结点入度之和等于边数,各结点出度之和也等于边数,因此任何有向图中,入度之和等于出度之和。
平行边和多重图
在上面所讲图的概念中,一个结点的度数可能大于1,但是任何一对结点间常常不多于一条边。我们把连接于同一对结点间的多条边称为是平行边。
定义7-1.4 含有平行边的任何一个图称为多重图
例如图7-1.5所示的均为多重图。在图7-1.5(a)中结点 𝑎a 和 𝑏b 之间有两条平行边,结点 𝑏b 和 𝑐c 之间有三条平行边,在结点 𝑏b 有两个平行的环。结点 𝑎a 的度数为3,结点 𝑐c 的度数为4,结点 𝑏b 的度数为9。在图7-1.5(b)中,只有结点 𝑣1v1 和 𝑣2v2 之间有两条平行边。这是因为该有向图中,(𝑣1,𝑣2)(v1,v2) 与 (𝑣2,𝑣1)(v2,v1) 认为是不同的结点对。
今后我们把不含有平行边和环的图称作简单图。
定义7-1.5 简单图和完全图
简单图 𝐺=(𝑉,𝐸)G=(V,E) 中,若每一对结点间都有边相连,则称该图为完全图。有 𝑛n 个结点的无向完全图记作 𝐾𝑛Kn,其边数为 𝑛(𝑛−1)22n(n−1)。
定理7-1.4 无向完全图的边数
证明:在 𝐾𝑛Kn 中,任意两点间都有边相连,𝑛n 个结点中任取两点的组合数为: 𝐶(𝑛,2)=𝑛(𝑛−1)2C(n,2)=2n(n−1) 故 𝐾𝑛Kn 的边数为 ∣𝐸∣=𝑛(𝑛−1)2∣E∣=2n(n−1)。
补图的定义
给定一个图 𝐺G,可以通过添加没有连接的边,将其补成一个具有相同结点的完全图。补成的图称为 𝐺G 的补图,记作 𝐺′G′。例如,图7-1.6中(a)和(b)互为补图。
子图和生成子图
定义7-1.7 子图和生成子图
设图 𝐺=(𝑉,𝐸)G=(V,E),若图 𝐺′=(𝑉′,𝐸′)G′=(V′,E′) 且 𝑉′⊆𝑉V′⊆V,𝐸′⊆𝐸E′⊆E,则称 𝐺′G′ 是 𝐺G 的子图。若子图包含 𝐺G 的所有结点,则称该子图为 𝐺G 的生成子图。

子图的补图
定义7-1.8 子图的补图
设 𝐺=(𝑉′,𝐸′)G=(V′,E′) 是图 𝐺=(𝑉,𝐸)G=(V,E) 的子图,若定义另外一个图 𝐺′′=(𝑉′′,𝐸′′)G′′=(V′′,E′′) 使得 𝐸′′=𝐸−𝐸′E′′=E−E′,且 𝑉′′V′′ 中仅包含 𝐸′′E′′ 的边所关联的结点,则称 𝐺′′G′′ 是子图 𝐺′G′ 的相对于图 𝐺G 的补图。例如,图7-1.7中,图(c)是图(b)相对于图(a)的补图。而图(b)不是图(c)相对于图(a)的补图,因为图(b)中有结点c。

图的同构
定义7-1.9 图的同构
设图 𝐺=(𝑉,𝐸)G=(V,E) 及图 𝐺′=(𝑉′,𝐸′)G′=(V′,E′),如果存在一一对应的映射 𝑔:𝑉→𝑉′g:V→V′,且 (𝑣,𝑤)∈𝐸(v,w)∈E 当且仅当 (𝑔(𝑣),𝑔(𝑤))∈𝐸′(g(v),g(w))∈E′,则称 𝐺G 与 𝐺′G′ 同构,记作 𝐺≈𝐺′G≈G′。
从图7-1.9的(c)与(d)中可以看到此两图在结点间存在着一一对应映射 𝑔:𝑔(𝑎)=𝑢1,𝑔(𝑏)=𝑢2,𝑔(𝑐)=𝑢3,𝑔(𝑑)=𝑢4g:g(a)=u1,g(b)=u2,g(c)=u3,g(d)=u4,且有:(𝑎,𝑐),(𝑎,𝑏),(𝑏,𝑑),(𝑎,𝑑)(a,c),(a,b),(b,d),(a,d) 分别与 (𝑢1,𝑢3),(𝑢1,𝑢2),(𝑢2,𝑢4),(𝑢1,𝑢4)(u1,u3),(u1,u2),(u2,u4),(u1,u4) 一一对应。
分析本例还可以知道,此两图的结点度数也分别对应相等,如表7-1.1所示。
| 结点 | 度数 |
|---|---|
| a | 2 |
| b | 3 |
| c | 1 |
| d | 2 |
综上所述,可以得到两图同构的一些必要条件:
- 结点数目相同;
- 边数相等;
- 度数相同的结点数目相等。
但这些条件并非充分条件。例如,图7-1.10中(a)和(b)满足上述条件,但它们并不同构。
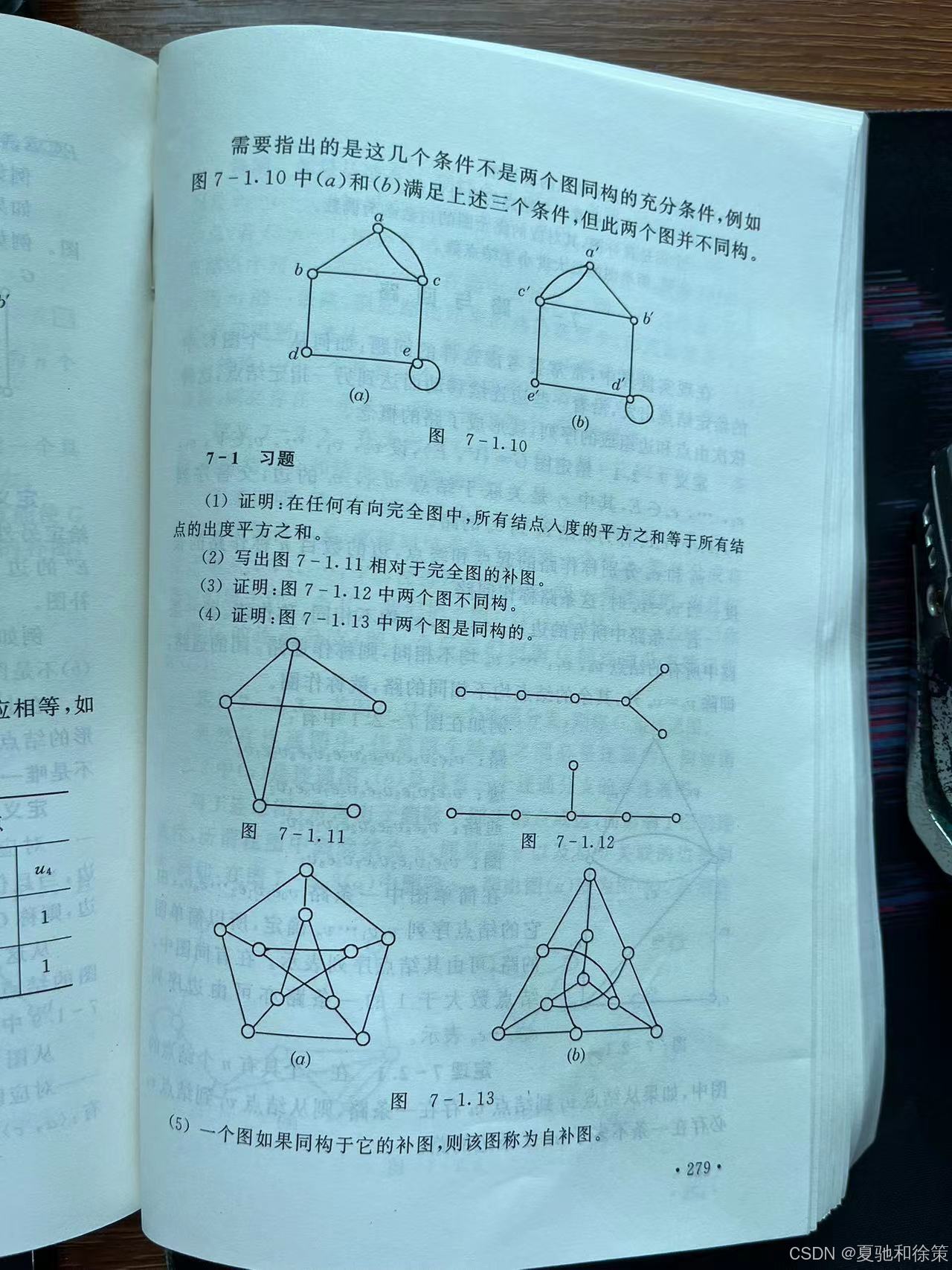
习题
- 证明:在任何有向完全图中,所有结点入度的平方之和等于所有结点的出度平方之和。
- 写出图7-1.11相对于完全图的补图。
- 证明:图7-1.12中两个图不同构。
- 证明:图7-1.13中两个图是同构的。
- 一个图如果同构于它的补图,则称该图为自补图。


2024/7/30日补充更新
我的笔记:


































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










