[图+最短路+模板] 五大最短路常用模板

已于 2024-11-26 00:37:25 修改
阅读量913 收藏 9
点赞数 1
分类专栏： -----图论----- 文章标签： 最短路 模板
于 2020-10-29 19:41:35 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/yl_puyu/article/details/109336000
版权

文章目录

0. 前言

重点在于代码实现
在这里插入图片描述
一些好的总结博文：

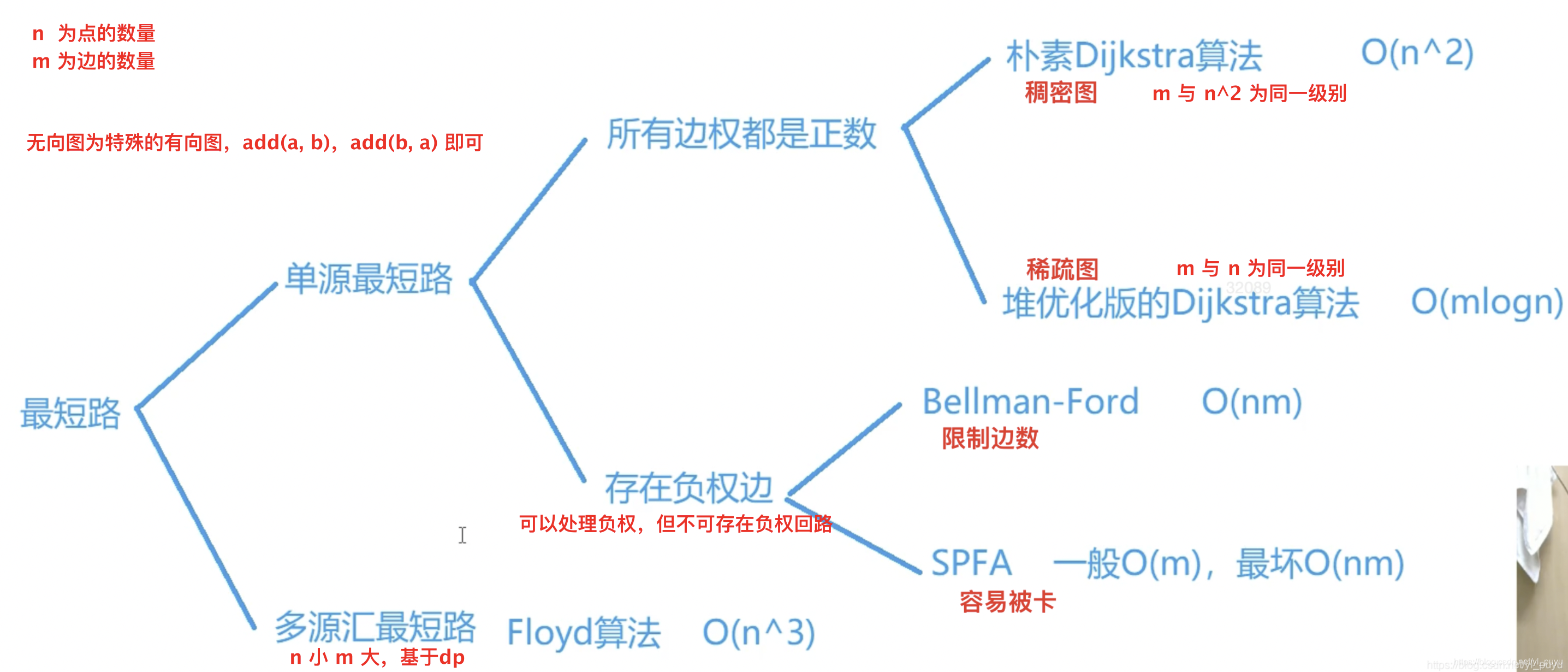
图论中最短路问题一般有两大类，然后在这两大类的基础上再细分为几个子项，下面简单梳理下知识点，总共 5 大最短路算法：

  • 单源最短路： 源点，就是起点的意思。汇点，就是终点的意思。从一个点到所有点的最短距离。例，求解 1 号点到 n 号点的最短路，那么我们可以求解出从 1 号点到 n - 1 号点的所有最短路。显然，从 1 号点到 n 号点的最短路也就随之确定。
    • 针对所有边权都是正数，有两大经典算法适用于不同场景：
      • 朴素 D i j k s t r a Dijkstra Dijkstra 算法：时间复杂度 O ( n 2 ) O(n^2) O(n2)，约定 n n n 为点的数量， m m m 为边的数量。能够发现，该算法时间复杂度与边数无关，更适合于稠密图的最短路计算，即题目数据范围大约是边数 m m m 和 n 2 n^2 n2 是同一个级别的。
      • 堆优化 D i j k s t r a Dijkstra Dijkstra 算法：时间复杂度 O ( m l o g n ) O(mlogn) O(mlogn)，如果稠密图来使用该算法，可以推公式： O ( n 2 l o g n ) O(n^2logn) O(n2logn)，比朴素版的还要高一些。其更适合稀疏图的最短路计算。
    • 存在负权边，也是两大经典算法：
      • B e l l m a n − F o r d Bellman-Ford Bellman−Ford 算法：时间复杂度 O ( n m ) O(nm) O(nm)，可以用来求解有步数限制的最短路问题。
      • S P F A SPFA SPFA 算法：一般情况平均时间复杂度 O ( m ) O(m) O(m)，最坏情况 O ( n m ) O(nm) O(nm)。时间复杂度相当优秀，应用范围很广，没有负环大多都可以让它求解，而一般的图论问题是不带负环的， 99 % 99\% 99% 以上。但是 S P F A SPFA SPFA 并不是什么问题都能解决。例如，求解不经过 k 条边的最短路只能采用 BF 最短路来做。后续遇见习题来针对性练习。
  • 多源汇最短路： 现在不是一个起点了，而是很多个询问，来任选两个点，求出这两点的最短路距离是多少。仅有一个经典算法：
    • 不区别正负边权，但是不能存在负环
      • F l o y d Floyd Floyd 算法：时间复杂度， O ( n 3 ) O(n^3) O(n3)，大多 n ⩽ 300 n\leqslant 300 n⩽300 左右很实用，很简单。

至此，只需要理解不同对应的情况应当采用什么算法即可。具体需要针对题目中去练习。

最短路算法的难点不在于模板，不在于裸题。而是，如何 建图，如何将原问题抽象成点、边、最短路的问题，然后再采用模板进行求解。

接下来会针对这 5 大最短路算法进行对应模板题及代码演示，不进行原理证明，网上太多了，大家随意去找，我只会总结解题的思路和方法及代码展示。

1. 朴素 Dijkstra 算法求最短路

849. Dijkstra求最短路 I

在这里插入图片描述

要点： 单源最短路、稠密图、邻接矩阵

思路：

  • 初始化距离矩阵 dist[1] = 0 代表 1 号点自己到自己的距离为 0，dist[i] = INA_MAX (i != 1)，dist[i] 数组代表单源点 1 号点到第 i 点的最短路。
  • 循环 n 次，每次确定 1 个 1 号点到该点的最短路。将已确定最短路的点划分为一个集合记为 s，并找到不在集合 s 中且距离最近的点 t ，即 dist 数组中数值最小的一个 ，将加入到 s 中，然后用该点 t 更新其它点的距离。
  • 基于贪心思想，该方法可证明其正确性，严格证明自行百度~

时间复杂度分析：

  • for 循环 n n n 次
  • 内层，找最小值循环 n − 1 n - 1 n−1 次，更新循环 n n n 次
  • 总共 O ( n 2 ) O(n^2) O(n2)

注意点：

  • 重边处理： 多条边仅保留一条长度最短的边即可。
  • 自环处理： 权值为正的自环不会出现在最短路中，故可以处理正自环问题。同理 g[a][a] = 0 表示 a 到自己 a 的距离为 0，理论上来讲是正确的。但是 其实 g[a][a] 等于任意正数均可，由于其本身为自环，是不可能参与到最短路答案中的。
  • 包括其他最短路问题也是这样处理的

代码：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 505;

int n, m;
int g[N][N], dist[N];
bool st[N];

int dijkstra() {
	// 这里不需要一定设置为 0x3f3f3f3f 作为无效距离，即不需要和 g 保持一致
	// 但需要大于所有边权之和
    memset(dist, 0x3f, sizeof dist);	
    dist[1] = 0;
    
    for (int i = 0; i < n; ++i) {
        int t = -1;
        for (int j = 1; j <= n; ++j)    // 找最小值
            if (!st[j] && (t == -1 || dist[t] > dist[j]))   // 未确定最短路，且距离最小
                t = j;
		
		if (t == n) break;        

        st[t] = true;
        
        // 这一步实际上也是只修改了 j 的出边，只不过遍历了所有的点，不可达点就不被修改，是INF值
        for (int j = 1; j <= n; ++j) 
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    
    return dist[n];
}

int main() {
    cin >> n >> m;
    // memset(g, 0x3f, sizeof g);		// 均可
    for (int i = 1; i <= n; i ++ ) 
        for (int j = 1; j <= n; j ++ ) 
            if (i == j) g[i][j] = 0;
            else g[i][j] = 0x3f3f3f3f;
    
    while (m --) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    cout << dijkstra() << endl;
    return 0;
}

2. 堆优化 Dijkstra 算法求最短路

850. Dijkstra求最短路 II

在这里插入图片描述

要点： 单源最短路、稀疏图、邻接表

思路：

  • 稀疏图，即若 n 是 1e5 的话，朴素版 dijkstra 时间复杂度就成了 1 0 10 10^{10} 1010，则时间必爆。
  • 分析整个朴素版代码，能发现：
    • 将 t 加入集合 s 时间复杂度 O ( 1 ) O(1) O(1) 的，一共循环了 n 次。
    • 用 t 更新其它点的距离，其实是遍历了所有的边，则计算量为 m 次。但在第一步，寻找 s 中距离最近的点需要遍历所有的点，即遍历 n 次才能够找到。在一堆数中寻找一个最小的数，就可以采用堆来寻找。那么就能在 O ( 1 ) O(1) O(1) 的时间找到最小值。但是，在堆中修改一个数的时间复杂度是 O ( l o g n ) O(logn) O(logn) 的，所有总共需要更新 m 次，所有总的时间复杂度为 ( m l o g n ) (mlogn) (mlogn) 的算法。
    • 但是，采用 STL 优先队列直接进行 push 操作，堆中可能会存在冗余备份，这是重边造成的，稀疏图也不需要处理重边，自环，算法保证重边不影响结果。例如，1–>2 存在两条边，权重分别为 2，3，那么在遍历到点 1 时，2 号点就会组织成 {2, 2} 、{3, 2} 全部放入堆中。但是在弹出堆头时还是会弹出 dist 最小的 {2,2}，并且将其标记为 st[2] 为 true，代表 2 号点的最短路已经找到为 dist[2]，此后是不会修改 st[2] 为 false，该点将永久确定。所以下一次再弹出 {3,2} 时，我们已经找到了 2 号点的最短路，所以直接 continue 就行了。这样的话我们堆中最坏需要存所有的边关系，所以时间复杂度也退化成了 O ( m l o g m ) O(mlogm) O(mlogm)

有关大佬分析：

在循环里面，我们只在 if( d[j] > distance + w[i]) 时才去做 push 操作；目的是为了减少重复的点放入堆里面；为什么可以这样做，可以这样理解： 我们一开始初始化 dist[] 为0x3f，即除了 1 号点，其它点在这时都是不可以到达 1 号点的意思；然后，如果点 i 可以到达 1 号点；那么一定有一次会执行push() 操作；这样 i 号点就被放进堆里面了； 以后只有当产生更小距离的点才有必要去更新 i 号点，即 push() 操作。换句话说，堆里面存的是目前已经连通 1 号点的结点信息。


首先看 while 循环次数，就是 q.size() 的大小，q.size() 的大小由内层循环 q.push() 决定，push 是在遍历边时才可能发生的，最多等于边数，所以外层最多 m 次，所以是有冗余的结果在里面堆中的；内层循环，q.pop() 最坏时 O(lgm); 总的循环次数： m(lgm) + m; 然后 m < n^2; 所以 lgm < 2lgn; 所以时间复杂度可以写成 O(mlogn); 如果变数 m 很大，接近 n^2 的话，就不如朴素的了。

代码：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

typedef pair<int, int> PII;		// 堆中 3维护距离需要知道节点编号

const int N = 1e6+5;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++; 
}

int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    // 以下为猜测~
    // 设置起点。单源最短路的性质，若为 dist[2]=0，则是 2 到任意点的最短路
    dist[1] = 0;		
    
    priority_queue<PII, vector<PII>, greater<PII>> heap;    // 小根堆
    heap.push({0, 1});                                      
    
    while (heap.size()) {
        auto t = heap.top();                                // 选出距离最短的点
        heap.pop();
        
        int v = t.second, d = t.first;
        
        if (st[v]) continue;
        st[v] = true;
        
        // 遍历所有点的所有边，就是遍历了整个图的所有边
        for (int i = h[v]; i != -1; i = ne[i]) {            // 遍历该点的所有邻边
            int j = e[i];
            if (dist[j] > d + w[i]) {						// 当前距离大于从t过来的距离，更新
                dist[j] = d + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    
    return dist[n];
}

int main() {
    memset(h, -1, sizeof w);
    
    cin >> n >> m;
    
    while (m --) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    cout << dijkstra() << endl;
    
    return 0;
}

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e6+5;

int n, m;
int e[N], w[N], ne[N], h[N], idx;
int d[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

// 重写仿函数，自定义 pair 排序，实现 greater<PII> 等价的基础功能
struct cmp {
    bool operator()(PII a, PII b) {
        if (a.first == b.first) return a.second > b.second;     
        return a.first > b.first;
    }
};

// 结构体，实现 pair 的基本功能
// 自定义结构类型，priority_queue<Node> heap; 声明即可
// 也可以 priority_queue<Node, vector<Node>, cmp> heap;      
// cmp 是重写仿函数的结构体，在此不能单单是函数指针
struct Node {
    int first, second;
    bool operator<(const Node a) const {      // 得加上 const，常成员函数，变量里面加不加const 均可
        if (first == a.first) return second > a.second;
        return first > a.first;
    }
};

int dijkstra() {
    memset(d, 0x3f, sizeof d);
    
    // priority_queue<PII, vector<PII>, greater<PII> > heap;       // 声明小顶堆
    // priority_queue<PII, vector<PII>, cmp> heap;
    priority_queue<Node> heap;
    d[1] = 0;
    heap.push({d[1], 1});
    
    while (heap.size()) {
        auto t = heap.top(); heap.pop();
        
        int dist = t.first, idx = t.second;
        
        if (st[idx]) continue;
        st[idx] = true;
        
        for (int i = h[idx]; i != -1; i = ne[i]) {
            int j = e[i];
            if (d[j] > dist + w[i]) {
                d[j] = dist + w[i];
                heap.push({d[j], j});
            }
        }
    }
    if (d[n] == 0x3f3f3f3f) return -1;
    return d[n];
}



int main() {
    
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    
    while (m -- ) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    
    int res = dijkstra();
    printf("%d\n", res);
    
    
    /*
    // priority_queue<PII, vector<PII>, greater<PII> > heap;
    priority_queue<PII, vector<PII>, cmp> q;
    q.push({1, 2});
    q.push({1, 3});
    q.push({1, -1});
    q.push({-1, 2});
    q.push({3, 2});
    
    while (q.size()) {
        auto t = q.top(); q.pop();
        cout << t.first << ' ' << t.second << endl;
    }
    */
    
    return 0;
}

3. Bellman-Ford 算法求最短路

853. 有边数限制的最短路

经典 B e l l m a n − F o r d Bellman-Ford Bellman−Ford 算法，该模板题，只能拿它来做。

其特别擅长解决有边数限制的最短路问题。
在这里插入图片描述

要点： 单源最短路、负权边、存在负环、稀疏图 / 稠密图、结构体

思路：

  • 迭代 n n n 次，每次循环所有边 a , b , w a,b,w a,b,w，代表存在一条从 a a a 走向 b b b 的边，权重为 w w w。所以在这的边的存储方式就不需要邻接表了，只要能够让我们遍历到所有的边，我们就可以选择这样的存储方式。所以，我们可以直接开一个结构体数组来存储，傻瓜式存边。 循环所有边，就是遍历这个结构体数组就可以了。
  • 遍历过程中，更新边的方式为 d i s t [ b ] = m i n ( d i s t [ b ] , b a c k u p [ a ] + w ) dist[b]=min(dist[b],backup[a]+w) dist[b]=min(dist[b],backup[a]+w)，和 d i j k s t r a dijkstra dijkstra 算法更新方式类似。即，查看从 1 号点走到 a a a 号点，再从 a a a 号点走到 b b b 号点的路径，是不是比 1 号点直接走到 b b b 号点的路径短。若短，则直接更新 1 号点到 b b b 点的路径。
  • 在此的 backup 数组十分重要，它是上一次 d i s t dist dist 数组的一个备份数组，因为我们需要遍历所有的边，如果当前边更新了，在 d i s t dist dist 数组中变短了，那么后面从该更新点出去的边也可能在本次循环中也被更新，这样就会发生串联效应，影响到后面的点了，就不能保证。所以我们采用上一次备份数组进行距离更新，这样就不会发生串联效应了。
  • 如下图，如果直接采用 d i s t dist dist 数组进行更新，那么如果 k k k 等 1，指的是我们仅经过 1 条边，到 3 号点的最短路径应该是 3，但是 d i s t dist dist 数组一开始将 1–>2 这条边的最短路更新后，它接着再去拿更新过的 d i s t [ 2 ] = 1 dist[2]=1 dist[2]=1 去更新 2–>3 这条边，那么就直接将 d i s t [ 3 ] = 2 dist[3]=2 dist[3]=2 更新了。那么我们最终返回的就返回了 d i s t [ 3 ] = 2 dist[3]=2 dist[3]=2 这个错误答案了， 实际上只经过一条边是无法从 1–>2–>3 的，但是由于串联效应的发生导致了这种错误的更新情况。所以，我们每次都需要用上一次的 d i s t dist dist 数组的备份数组来进行松弛操作，这样的话， b a c k u p [ 2 ] backup[2] backup[2] 就是无穷，那么 b a c k u p [ 2 ] + 1 > d i s t [ 3 ] backup[2]+1 > dist[3] backup[2]+1>dist[3]，即 I N F + 1 > I N F INF+1>INF INF+1>INF 更新失败，则 d i s t [ 3 ] dist[3] dist[3] 就不会被错误更新为 2。 关键需要理解不超过 k k k 步这个概念。
    - [外链图片转存失败,源站可能有防盗在这里插入!链机制,建描述]议将图片上https://传(imblog.csnmg.cn/2020AOkZ1029155727728.png#pic_cener)(https://img-1blog.csdnimg.cn/20201029155727728.png#pic_center)]
  • 循环完之后，算法证明了所有边都满足， d i s t [ b ] ⩽ d i s t [ a ] + w dist[b] \leqslant dist[a]+w dist[b]⩽dist[a]+w。这个被称为三角不等式，更新的过程被称为松弛操作。

注意：

  • 如果有负权回路的话， B e l l m a n − F o r d Bellman-Ford Bellman−Ford 算法不一定能求解到最短路，因为它可以在负权回路中转无穷多圈再出去，那么从 1 号点到 n n n 号点之间的最短路就是负无穷了。只要负环所在路径不与 n n n 号点连通，则还是不影响从 1 号点到 n n n 号点的最短路求解的。
  • 同时 B e l l m a n − F o r d Bellman-Ford Bellman−Ford 算法可以求出来是否存在负权回路，我们所做一次松弛操作都是有实际意义的，比如，我们当前迭代了 k k k 次，那么 d i s t dist dist 数组目前的实际意义是从 1 号点，经过不超过 k k k 条边走到每个点的最短距离。 那么，当我们再第 n n n 次迭代又更新了某些边的话，那就说明存在一条边的个数是 n n n 的最短路，那么这条最短路总共就有 n + 1 n+1 n+1 个点，那么由抽屉原理得到，必然两个点的编号一样，则一定存在一条环，且由于它是更新过的，所以一定是负环。
  • 故，只要第 n n n 次迭代有更新，则存在负环。所以可以用它来找负环，但是一般不用它来做，时间复杂度较高，一般采用 S P F A SPFA SPFA 来找负环。
  • 在最后判断能否到达 n n n 号点时是 if(dist[n] > INF_MAX / 2) 而不仅仅是 if(dist[n] == INF_MAX) 判断，因为 INF_MAX 其实也只不过是个数，当有一条负权边与 n n n 号点相连，且两者同时不能从 1 号点到达时，理论上来讲应该 dist[n] = INF_MAX，但是这个无穷要比 INF_MAX 小，因为它被负权边更新过，所以不要直接用初始化的无穷来直接进行 == 判断，这点很重要，很常用。
    在这里插入图片描述

代码：

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 505, M = 1e5+10;

int n, m, k;
int dist[N], backup[N];

struct Edge {
    int a, b, w;
}edges[M];

int bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < k; ++i) {				// 注意在此的边数限制
        memcpy(backup, dist, sizeof dist);      // 备份backup数组，用以更新，避免串联
        for (int j = 0; j < m; ++j) {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            dist[b] = min(dist[b], backup[a] + w);
        }
    }
    
    if (dist[n] > 0x3f3f3f3f / 2) return -1;    // 最多也就减500*10000
    return dist[n];
}

int main() {
    cin >> n >> m >> k;
    
    for (int i = 0; i < m; ++i) {
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }
    
    int t = bellman_ford();
    
    if (t == -1) puts("impossible");
    else cout << t << endl;
    return 0;
}

4. SPFA 算法求最短路

851. spfa求最短路

在这里插入图片描述

要点： 单源最短路、负权边、无负环、稀疏图 / 稠密图

思路：

  • 优化 B e l l m a n − F o r d Bellman-Ford Bellman−Ford 更新的过程 d i s t [ b ] = m i n ( d i s t [ b ] , b a c k u p [ a ] + w ) dist[b]=min(dist[b],backup[a]+w) dist[b]=min(dist[b],backup[a]+w)，我们能够发现，当且仅当 b a c k u p [ a ] backup[a] backup[a] 变小，才会导致 d i s t [ b ] dist[b] dist[b] 更新。我们可以采用宽搜的思想，来优化更新的情况：
    • 迭代时将起点放入队列，只要队列不空，队列中所有存的都是所有变小的节点，用这些变小的节点来更新他们所对应的出边才有意义。如果出边也随之变小了就将出边点也入队，如果该点已经在队列中了，那么就不用重复加入了
    • 本质就是一个点更新过谁，才将其拿来更新别人。如果该点没有更新过的话，再去更新别人是没有意义的。等价于只有我自己变小了，我后面的才会变小。
  • s p f a spfa spfa 在单源最短路，可以代替堆优化版 d i j k s t r a dijkstra dijkstra 算法，故 s p f a spfa spfa 应用十分广泛，且效率很高，一般为 O ( m ) O(m) O(m)。容易被卡成 O ( n m ) O(nm) O(nm)，被卡掉的话换成堆优化 d i j k s t r a dijkstra dijkstra 即可。

注意：2024年11月26日00:19:45 有新的理解。

  • 在做 [M最短路] lc743. 网络延迟时间(spfa最短路+单源最短路) 的时候发现，自己乱写的最短路也能过？实际上仔细对比一下 spfa 和 堆优化 dij 来说，spfa 就是它的优化版。
  • 堆优化 dij，一定需要用优先队列吗？实际上也不需要。因为最短路的边，一定会被遍历到，且用来更新答案。只不过中间用了很多很多冗余更新罢了。
  • 这也是为什么不需要开优先队列，不需要去做 st 数组也能得到正确答案的原因。
    • 可以尝试将堆优化 dij 的优先队列改为普通队列，将 st 数组直接删掉，在小数据的题目中依旧可以通过。

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e6+5;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

// 和堆优化dijkstra算法很相似，直接cv过去就能过掉
int spfa() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    queue<int> q;
    q.push(1);
    st[1] = true;
    
    while (q.size()) {
        int t = q.front();
        q.pop();
        
        st[t] = false;
        
        for (int i = h[t]; i != -1; i = ne[i]) {    // 更新t的所有出边
            int j = e[i];                           // j表示当前这个点        
            if (dist[j] > dist[t] + w[i]) {         
                dist[j] = dist[t] + w[i];           
                if (!st[j]) {                       // 可更新，入队
                    q.push(j);
                    st[j] == true;
                }
            }
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    
    while (m --) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    int t = spfa();
    if (t == -1) puts("impossible");
    else cout << t << endl;
    
    return 0;
}

852. spfa判断负环

在这里插入图片描述
要点： 单源最短路、负权边、带负环、稀疏图 / 稠密图

思路：

  • 在原有 s p f a spfa spfa 基础上多维护一个数组 c n t cnt cnt，其记录当前点的最短路经过的边数。当 d i s t [ x ] = d i s t [ t ] + w [ i ] dist[x] =dist[t]+w[i] dist[x]=dist[t]+w[i] 转移时， c n t [ x ] = c n t [ t ] + 1 cnt[x]=cnt[t]+1 cnt[x]=cnt[t]+1 也跟随转移。
  • 如果某次， c n t [ x ] ⩾ n cnt[x] \geqslant n cnt[x]⩾n 的话，则说明存在负环，不再赘述，抽屉原理。
  • 涉及到一些初始化数组的情况，更有利于理解各个算法的核心思想，将边缘操作抛弃。在代码中已经做了注释。
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

const int N = 1e5+5;

int n, m;
int e[N], h[N], w[N], ne[N], idx;
int dist[N];
int cnt[N];     // 记录边数
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

// spfa判断负环
bool spfa() {       
    // 在此已经不需要对其进行初始化了，只是判断是否有负环
    // 单源点即便初始化正无穷完毕，也会将dist[1]=0,现在是多源点，也要将dist[i]=0，所以不必要初始化了
    // 也可以这样理解
    // 没有进行dist数组初始化为0x3f3f3f3f，因为当前dist数组并不存储最短路径了，任何值都可，
    // 只要比存在负环造成的负无穷大要大即可，所以0就满足情况，使用默认值即可
    
    
    queue<int> q;
    for (int i = 1; i <= n; ++i) st[i] = true, q.push(i);   // 可能1号点到不了，起始点全部入队
    
    
    
    while (q.size()) {
        int t = q.front();
        q.pop();
        st[t] = false;
        
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            // 队列初始时将所有点都加入队列，所以负环一定会发生更新并且一定会发生死循环到达边数为n然后返回true
            if (!st[t]) {
                if (dist[j] > dist[t] + w[i]) {     
                    dist[j] = dist[t] + w[i];
                    cnt[j] = cnt[t] + 1;
                    
                    if (cnt[j] >= n) return true;
                    
                    if (!st[j]) {
                        q.push(j);
                        st[j] = true;
                    }
                }
            }
        }
    }
    return false;
}

int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    
    while (m --) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    if (spfa()) puts("Yes");
    else puts("No");
    
    return 0;
}

至此，单源最短路四大算法已经搞定~

5. Floyd 算法求最短路

854. Floyd求最短路

在这里插入图片描述

要点： 多源汇最短路、不存在负环、邻接矩阵

思路：

  • 邻接矩阵 d [ i ] [ j ] d[i][j] d[i][j] 存储所有的边、边权
  • 三重循环
    • k k k 从 1 到 n n n
    • i i i 从 1 到 n n n
    • i i i 从 1 到 n n n
    • 循环内更新 d [ i ] [ j ] = m i n ( d [ i ] [ j ] , d [ i ] [ k ] + d [ k ] [ j ] ) d[i][j]=min(d[i][j],d[i][k]+d[k][j]) d[i][j]=min(d[i][j],d[i][k]+d[k][j])
  • 循环结束， d [ i ] [ j ] d[i][j] d[i][j] 存储 i i i 到 j j j 最短路的长度
  • 算法原理基于动态规划
    • 状态表示： d [ k , i , j ] d[k,i,j] d[k,i,j] 表示经过前 k 个点作为中间点，从起点 i 到达终点 j j j 的最短距离。
    • 状态更新：以经过点 k、不经过点 k 进行集合划分。 d [ k , i , j ] = m i n ( d [ k − 1 , i , j ] , d [ k − 1 , i , k ] + d [ k − 1 , k , j ] d[k,i,j]=min(d[k-1,i,j],d[k-1,i,k]+d[k-1,k,j] d[k,i,j]=min(d[k−1,i,j],d[k−1,i,k]+d[k−1,k,j]，所以可以去掉最高维 k k k，将其优化掉即可。且 d[k] 完全依赖与 d[k-1]，所以一定要先循环 k。
    • 先循环 k，其中 i、j 的顺序可以任意颠倒。

注意：

  • 在下面代码中，判断从 a 到 b 是否是无穷大距离时，需要进行 if(t > INF/2) 判断，而并非是 if(t == INF) 判断，原因是 INF 是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，t 大于某个与 INF相同数量级的数即可。
  • 状态转移正确性证明。 由图论中的性质：最短路径的子路径仍然是最短路径。 比如一条从 a 到 e 的最短路 a->b->c->d->e 那么 a->b->c 一定是 a 到 c 的最短路 c->d->e 一定是 c 到 e 的最短路，反过来，如果说一条最短路必须要经过点 k，那么 i->k 的最短路加上 k->j 的最短路一定是 i->j 经过 k 的最短路。

以下分析来自资料 3 ：3. 针对Floyd算法优化空间做了详细总结： 最短路算法总结：Floyd，Dijkstra，Bellman-Ford，SPFA

一切的优化都不是想当然，一定是可以经得起推敲的！
在这里插入图片描述

时间复杂度：

  • 三重循环 O ( n 3 ) O(n^3) O(n3)。

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 205, INF = 1e9;

int n, m, Q;
int d[N][N];

void floyd() {
    for (int k = 1; k <= n; ++k)
        for (int i = 1; i <= n; ++i) 
            for (int j = 1; j <= n; ++j)	// 更改 i、j 的循环顺序也可
                    d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
            // d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k] + d[k-1][k][j]);
}

int main() {
    cin >> n >> m >> Q;
    
    for (int i = 1; i <= n; ++i) 
        for (int j = 1; j <= n; ++j) 
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;
            
    while (m --) {
        int a, b, w;
        cin >> a >> b >> w;
        d[a][b] = min(d[a][b], w);
    }
    
    floyd();
    
    while (Q --) {
        int a, b;
        cin >> a >> b;
        if (d[a][b] > INF / 2) puts("impossible");  // 判断无解，负权边问题
        else cout << d[a][b] << endl;
    }
    return 0;
}

6. 总结

图论入门级模板，没啥好总结的。多刷题，多练习即可。最为重要的是关注数据范围和时间复杂度。 简单总结如下：

  • n ≈ 300 n \approx 300 n≈300， m m m 很大的情况下， F l o y d Floyd Floyd 真的香
  • n ， m ≈ 100000 n，m \approx 100000 n，m≈100000， s p f a spfa spfa 堆优化 d i j k s t r a dijkstra dijkstra

牢记各个算法的应用场景和时间复杂度，

  • 注意 s p f a spfa spfa 它的应用很广泛，没负环就可用到
  • 注意 B e l l m a n − F o r d Bellman-Ford Bellman−Ford 在有步数限制的题目中求最短路的应用
  • 堆优化 d i j k s t r a dijkstra dijkstra 的来处理稀疏图
  • 朴素 d i j k s t r a dijkstra dijkstra 处理稠密图
最短路【模板】
Konnyaku
04-19 1266
Dijkstra算法和SPFA算法用于求最短路。（Floyd的话，还是算了吧） 最短路就是求两点之间的最短路径。 最短路径怎么求呢？ 更新就是了（松弛）。 先赋予厚望（先假设无穷大） 然后依次更新 通过起点1来比较哪条路到终点20最短 暂时选择这条绿色的路 继续比较 所以蓝色的路是最短的。 然后看一道纯模板题。 骑车比赛 Description 小信准备去参加骑车比赛，比赛在 n 个城市间...
三种最短路模板
算法小猪的博客
02-25 661
一、Floyd算法——只有五行代码的算法 算法思想： 从节点i到节点j的最短路径只有2种可能： 1)直接从节点i到节点j 2)从节点i经过若干个节点k到节点j 假设dis(i,j)为节点i到节点j的最短路径的距离 对于每一个节点k，我们检查dis(i,k)+dis(k,j) < dis(i,j)是否成立， 如果成立，证明从i到k再到j的路径比i直接到j的路径短. 于是dis(...
最短路模板（dijstra）
CoderZ的编程之路
03-10 598
#define INF 0Xfffffff const int Max=1000000; int map[Max][Max]; int dis[Max]; bool vis[Max]; void dijstra() { memset(vis,false,sizeof(vis)); int i,j,mark_num,temp; for(i=1;i<=n;i++) {
最短路问题(五个算法模板)
最新发布
2401_87934559的博客
03-29 1994
题目给定一个有向图，图中有 𝑛n 个点和 𝑚m 条边。图中可能存在重边和自环，所有边权均为正值。请你求出从 1 号点到 𝑛n 号点的最短距离。如果无法从 1 号点走到 𝑛n 号点，则输出 -1。
最短路（模板）
weixin_34387468的博客
12-31 136
Floyd 最短路 （时间复杂度O(N^3)，适用于出现负边权的情况，可以求任意两点间的最短路径） #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<algorithm> #include<cma...
最短路模板
Tom的博客
06-25 245
最短路分为：单源最短路，包括Dijkstra算法、Bellman-ford算法和SPFA算法；以及多源最短路，包括Floyd算法。
最短路 模板
wwhhff11
03-09 289
#include <iostream> #include <cstring> #include <cstdio> #include <queue> const int INF=0x3f3f3f3f; const int maxn=1005; using namespace std; int n,t,cnt[maxn],vis[maxn]; double e[maxn][maxn],dis[maxn]
【图论】最短路问题大合集，五种算法刷爆最短路问题。
m0_70875482的博客
10-22 957
思路：迭代n次，每次找到距离离起点最近的点，起点置为0，并且用距离最近的点更新其他点。题目：给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。输入格式：第一行包含整数 n 和 m。接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。输出格式：输出一个整数，表示 1 号点到 n 号点的最短距离。
算法工程师第五十三天（Floyd 算法精讲 A * 算法精讲 （A star算法）最短路算法总结 图论总结 ）
rgz147123的博客
09-02 984
决定了两种dfs的写法。这也是为什么很多录友看到不同的dfs写法，结果发现提交都能过的原因。而深搜还有细节，有的深搜题目需要用到回溯的过程，有的就不用回溯的过程，一般是需要计算路径的问题 需要回溯，如果只是染色问题（岛屿问题系列） 就不需要回溯。例如：
最短路问题（Dijkstra，Bellman_Ford，SPFA，Floyd，Johnson）
Q4043的博客
07-23 1134
图论中入门问题最短路径问题
数学建模 最短路问题
07-04
是一个关于数学建模的ppt 若大家需要有关方面的东西 可以作为参考
【大作业】城市地铁线路最短路规划及路径输出（满分）
繁凡さん的博客
07-15 6032
城市地铁线路规划完整大作业（思路分析+构造数据+代码+优化+算法分析）
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Ypuyu

如果帮助到你，可以请作者喝水~

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值