
在一个2*x2‘个方格组成的棋盘中,若怡有一个方格与其他方格不同,则称该方格为
特殊方格,且称该棋盘为一特殊棋盘。显然,特殊方格在棋盘上出现的位置有 4种情形
因而对任何k=0,有4‘种特殊棋盘。图2-4 申的特殊棋益是1=2时 16个特殊棋盘中的一个
在棋盘複盖问题中,要用图2-5 所示的 4种不同形态的工 型骨牌覆盖一个给定的特殊棋
盘上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个
2*x2*的棋盘覆盖中,用到的L 型骨牌个数恰为(45-1)/3。
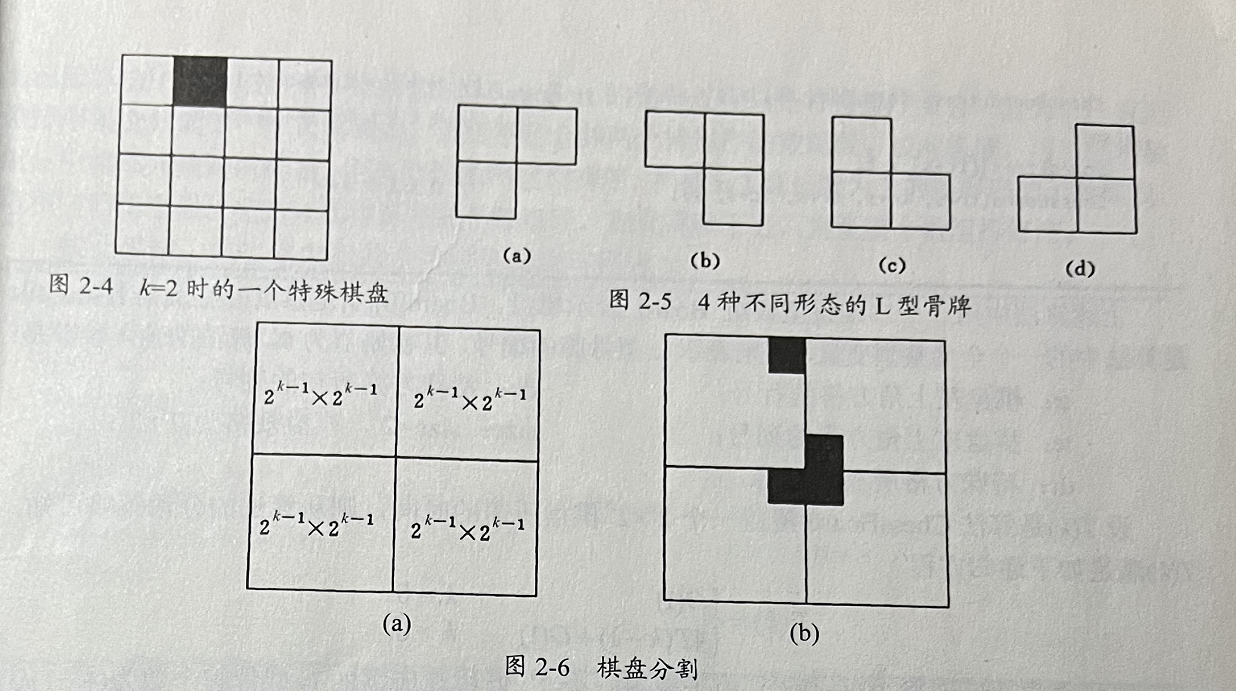
用分治策咯,可以设计解棋盘復盖问题的一个简捷的算法。当心0时,将2'x2*棋盛分
割为 4个25-x25!子棋盛,如图 2-6(a)所示。特殊方格必位于 4 个较小子棋盘之一中,其余3
个子棋盘中无特殊方格。为了将这 了个无特殊方格的子棋盘转化为特殊棋盘,可以用一个山
型骨牌覆盖这了个较小棋盘的会合处,如图2-6(所示,这了个子棋盘上被L型骨牌覆盖的方
格就成为该棋盘上的特殊方格,从而将原问题转化为 4个较小规模的棋盘覆盖问题。递归地使用
这种分割,直至棋盘简化为 1×1 棋盘。
实现这种分治策略的算法 Chess Board 如下:
void ChessBoard (int tr, int tc, int dr, int dc, int size) {
if (size ==1
return;
int t=tilet+,
s=size/2;
1/後盖左上角子棋盘
if (dr ‹tr+s && de‹tc+s)
ChessBoard (tr, tc, dr, dc, s);
else {
Board[tr+s-1][tc+s-1]=t;
ChessBoard(tr, tc, tr+s-1, tc+s-1, s);
if (dr < tr+s&& de ›= tc+s)
ChessBoard(tr, tc+s, dr, dc, s);
else {
Board[tr+s-11 tc+s] = t;
ChessBoard(tr, tc+s, tr+s-1, tc+s, s);
if (dr ›= tr+s && dc < tc+s)
ChessBoard (tr+s, tc, dr, dc, s);
else {
Board[tr+s][tc+s-1] = t;
ChessBoard(tr+s, tc, tr+s, tc+s-1, s);
if (dr ›= tr+s && dc ›= tc+s)
//L型骨牌号
//分割棋盘
//特殊方格在此栱盘中
//此栱盘中无特殊方格
//用七号山型骨牌覆盖右下角
//覆盖其余方格
//爱盖右上角子棋盘
//特殊方格在此棋盘中
//此棋盘中无特殊方格
//用七号L型骨牌覆盖左下角
//覆盖其余方格
//覆盖左下角子棋盘
//特殊方格在此棋盘中
//用七号山型骨牌覆盖右上角
//覆盖其余方格
//爱盖右下角子棋盘上述算法中用一个二维整型数组 Board 表示棋甜。BoarcroIrO1是棋盘的左上角方格。
是算法中的一个全局性型交量,用表示工 型骨牌的编号,其初始值为 0。算法的输入珍数是
切:棋盘左上角方格的行号;
dc:特殊方格所在的列号;
tc:棋盘左上角方格的列号;
size: size=2%,棋盘规格为 2*x2%,
dr:特殊方格所在的行号。
设TK是算法 ChessBoard 覆盖
一个2*x2*棋盘所需的时间,则从算法的分治策略可知,
『满足如下递归方程
(O(1)
k= 0
T(k) ={AT(k -1) + O()
解此递归方程可得

7(=0(45。由于覆盖一个242%棋盘所需的L 型骨牌个数为(4'-1/3
故算法 ChessBoard 是一个在渐近意义下最优的算法。


























 700
700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










