有趣算法之2.6 棋盘覆盖

2.6 棋盘覆盖

20200925

下面关于题目解释之类的图片均来自：https://www.bilibili.com/video/BV1o7411Q7GV?from=search&seid=11042594498287500570

参考链接：https://www.cnblogs.com/yinbiao/p/8666209.html

 

1.问题描述

覆盖情况大致如下图所示：

 

2.问题分析

根据题意，似乎给定一个2k X2k 的棋盘且且有一个特殊方格，就可以用上图中的L型骨牌进行覆盖。那么这个是一定的吗？我们来证明试试，结果如下：使用的是数学归纳法

 

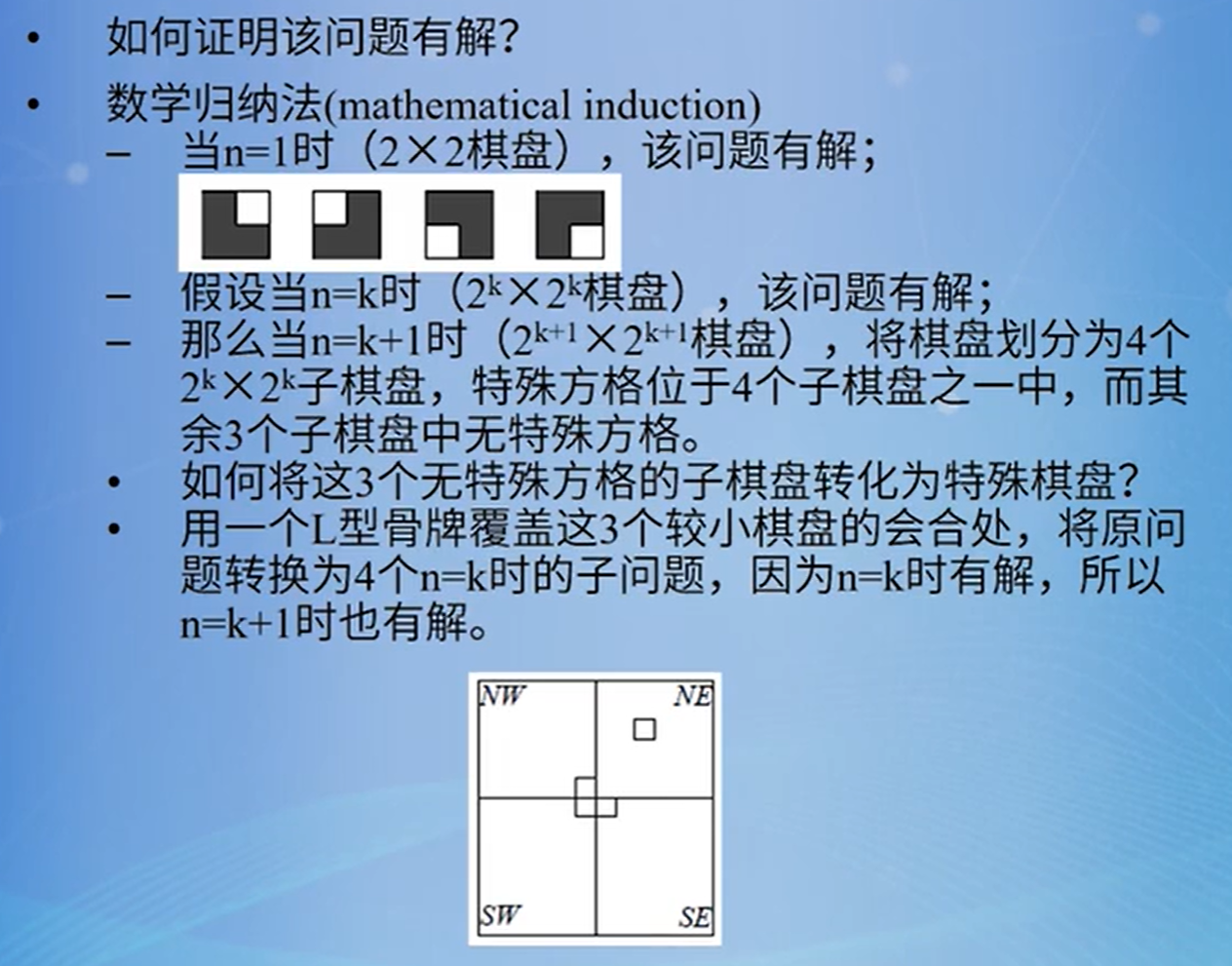
2.1.思路讲解

 

如下图，棋盘为16*16，特殊方格为绿色的。下面，我们利用分治思想对其进行划分：

设左上角为L_up区，右上角为R_up区，左下角为L_down区，右下角为R_up区，

1. 蓝色：划分为四个8*8的子棋盘。特殊方块在L_up区。R_up区、L_down区、R_up区都没有特殊方块，因此在他的对角设置一个特殊方块（蓝色），恰好能构成一个L型骨牌，也恰好可以在R_up区、L_down区、R_up区三个区也设置一个特殊方块，然后再进行划分；（这里我们主要以左上角为例进行不断的细分，其他的三个区类似）
2. 红色：将左上角划分为四个4*4的子棋盘，这次恰好有事特殊方块（绿色）在左上角，R_up区、L_down区、R_up区都没有特殊方块，可以类似步骤一在R_up区、L_down区、R_up区三个区的对角各设置一个特殊方块（红色），也恰好构成一个L型骨牌。
3. 黄色：再对左上角进行划分，为四个2*2的子棋盘。特殊方块这次在右下角，因此在其他三个区的对角一次设置一个特殊方块（黄色）。
4. 紫色：对右下角再次进行划分，为1*1的子棋盘。长度为1，停止划分。

注意：上面总是提到区域对角设置特殊方格，这个怎么理解呢？如下图，其实就是类似于这种斜对角的关系，假设当左上角区域没有特殊方块时，那么我们就应该在左上角区域的最右下角设置一个方块。其他的区域也类似。

 

3.代码实现

#include <stdio.h>
#define max 1024
int cb[max][max];//最大棋盘
int tile=0;//L型骨牌的编号

int chessboard(int tr,int tc,int dr,int dc,int size)
//tr，tc代表棋盘左上角的位置，dr ,dc代表特殊方格所在的行号和列号,size是棋盘大小，size=2^k
{
    if(size==1) return 0;//当棋盘大小为1时，停止划分
    int t=tile++;//L型骨牌号
    int s=size/2;//棋盘划分

    //开始标记特殊方块
    //左上角
    if(dr<tr+s && dc<tc+s){//特殊方块在左上角区域
        chessboard(tr,tc,dr,dc,s);//继续划分
    }
    else{//不在左上角，则开始标记特殊方块
        cb[tr+s-1][tc+s-1]=t;//特殊方块标记完毕
        chessboard(tr,tc,tr+s-1,tc+s-1,s);//标记完毕后，再次进行划分
    }
    //右上角
    if(dr<tr+s && dc>=tc+s){//特殊方块在右上角区域
        chessboard(tr,tc+s,dr,dc,s);//继续划分
    }
    else{//不在右上角，则开始标记特殊方块
        cb[tr+s-1][tc+s]=t;//特殊方块标记完毕
        chessboard(tr,tc+s,tr+s-1,tc+s,s);//标记完毕后，再次进行划分
    }
    //左下角
    if(dr>=tr+s && dc<tc+s){//特殊方块在左下角区域
        chessboard(tr+s,tc,dr,dc,s);//继续划分
    }
    else{//不在左下角，则开始标记特殊方块
        cb[tr+s][tc+s-1]=t;//特殊方块标记完毕
        chessboard(tr+s,tc,tr+s,tc+s-1,s);//标记完毕后，再次进行划分
    }
    //右下角
    if(dr>=tr+s && dc>=tc+s){//特殊方块在右下角区域
        chessboard(tr+s,tc+s,dr,dc,s);//继续划分
    }
    else{//不在右下角，则开始标记特殊方块
        cb[tr+s][tc+s]=t;//特殊方块标记完毕
        chessboard(tr+s,tc+s,tr+s,tc+s,s);//标记完毕后，再次进行划分
    }
}

int main()
{
    printf("请输入正方形棋盘的大小（行数）:\n");
    int n;
    scanf("%d",&n);
    printf("请输入在%d*%d棋盘上特殊方块的位置:\n",n,n);
    int i,j,k,l;
    scanf("%d %d",&i,&j);
    printf("特殊方块位置输入完毕，特殊方块的值为-1\n");
    cb[i][j]=-1;
    chessboard(0,0,i,j,n);
    for(k=0;k<n;k++){
        printf("%2d",cb[k][0]);
        for(l=1;l<n;l++){
            printf("%4d",cb[k][l]);
        }
        printf("\n");
    }
     return 0;
}

运行结果：