1-4 真值表与等价公式

 

1-4 真值表与等价公式

真值表的定义

定义1-4.1 在命题公式中，对其分量指派真值的各种可能组合，就确定了这个命题公式的各种真值情况，把它汇列成表，就是命题公式的真值表。

例题及其真值表

例题1 构造 𝑃∨𝑄P∨Q 的真值表。

P	Q	𝑃∨𝑄P∨Q
T	T	T
T	F	T
F	T	T
F	F	F

例题2 给出 (𝑃∧𝑄)∨¬𝑃(P∧Q)∨¬P 的真值表。

P	Q	¬𝑃¬P	𝑃∧𝑄P∧Q	(𝑃∧𝑄)∨¬𝑃(P∧Q)∨¬P
T	T	F	T	T
T	F	F	F	F
F	T	T	F	T
F	F	T	F	T

例题3 给出 (𝑃∧𝑄)∨(¬𝑃∧¬𝑄)(P∧Q)∨(¬P∧¬Q) 的真值表。

P	Q	¬𝑃¬P	¬𝑄¬Q	𝑃∧𝑄P∧Q	¬𝑃∧¬𝑄¬P∧¬Q	(𝑃∧𝑄)∨(¬𝑃∧¬𝑄)(P∧Q)∨(¬P∧¬Q)
T	T	F	F	T	F	T
T	F	F	T	F	F	F
F	T	T	F	F	F	F
F	F	T	T	F	T	T

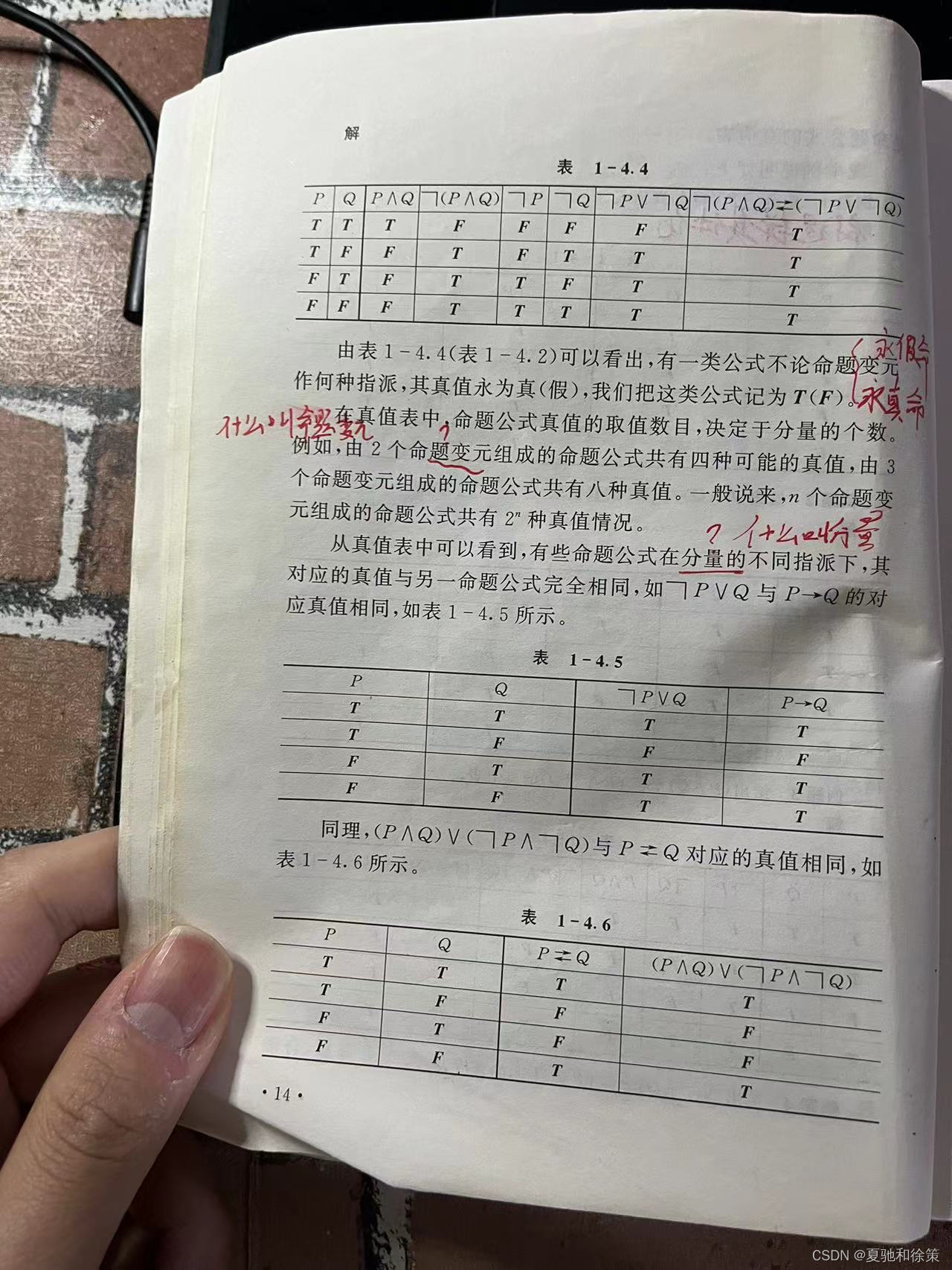
例题4 给出 ¬(𝑃∧𝑄)=(¬𝑃∨¬𝑄)¬(P∧Q)=(¬P∨¬Q) 的真值表。

P	Q	𝑃∧𝑄P∧Q	¬(𝑃∧𝑄)¬(P∧Q)	¬𝑃¬P	¬𝑄¬Q	¬𝑃∨¬𝑄¬P∨¬Q	¬(𝑃∧𝑄)=(¬𝑃∨¬𝑄)¬(P∧Q)=(¬P∨¬Q)
T	T	T	F	F	F	F	T
T	F	F	T	F	T	T	T
F	T	F	T	T	F	T	T
F	F	F	T	T	T	T	T

从表中可以看到，有一类公式不论命题变元作何种指派，其真值永为真或永为假，我们把这类公式分别记为T或F。一般来说，n个命题变元组成的命题公式共有 2𝑛2n 种真值情况。

等价公式

定义1-4.2 给定两个命题公式A和B，设P1, P2, ... 为所有出现在A和B中的原子变元，若给P1, P2, ... 任一组真值指派时，A和B的真值都相同，则称A和B是等价的或逻辑相等，记作 𝐴≡𝐵A≡B。

例题5 证明 𝑃≡𝑄≡(𝑃→𝑄)∧(𝑄→𝑃)P≡Q≡(P→Q)∧(Q→P)。

P	Q	𝑃→𝑄P→Q	𝑄→𝑃Q→P	(𝑃→𝑄)∧(𝑄→𝑃)(P→Q)∧(Q→P)	𝑃≡𝑄P≡Q
T	T	T	T	T	T
T	F	F	T	F	F
F	T	T	F	F	F
F	F	T	T	T	T

从表中可以看到， 𝑃≡𝑄P≡Q 与 (𝑃→𝑄)∧(𝑄→𝑃)(P→Q)∧(Q→P) 的真值相同，故命题得证。

命题定律

表1-4.8列出的命题定律都可以用真值表予以验证。

双重否定律

• 𝑃≡¬¬𝑃P≡¬¬P

交换律

• 𝑃∨𝑄≡𝑄∨𝑃P∨Q≡Q∨P
• 𝑃∧𝑄≡𝑄∧𝑃P∧Q≡Q∧P

结合律

• (𝑃∨𝑄)∨𝑅≡𝑃∨(𝑄∨𝑅)(P∨Q)∨R≡P∨(Q∨R)
• (𝑃∧𝑄)∧𝑅≡𝑃∧(𝑄∧𝑅)(P∧Q)∧R≡P∧(Q∧R)

分配律

• 𝑃∧(𝑄∨𝑅)≡(𝑃∧𝑄)∨(𝑃∧𝑅)P∧(Q∨R)≡(P∧Q)∨(P∧R)
• 𝑃∨(𝑄∧𝑅)≡(𝑃∨𝑄)∧(𝑃∨𝑅)P∨(Q∧R)≡(P∨Q)∧(P∨R)

吸收律

• 𝑃∨(𝑃∧𝑄)≡𝑃P∨(P∧Q)≡P
• 𝑃∧(𝑃∨𝑄)≡𝑃P∧(P∨Q)≡P

德摩根律

• ¬(𝑃∧𝑄)≡¬𝑃∨¬𝑄¬(P∧Q)≡¬P∨¬Q
• ¬(𝑃∨𝑄)≡¬𝑃∧¬𝑄¬(P∨Q)≡¬P∧¬Q

条件转化

• 𝑃→𝑄≡¬𝑃∨𝑄P→Q≡¬P∨Q

双条件等价

• 𝑃↔𝑄≡(𝑃→𝑄)∧(𝑄→𝑃)P↔Q≡(P→Q)∧(Q→P)

例题6 验证吸收律 𝑃∨(𝑃∧𝑄)≡𝑃P∨(P∧Q)≡P 和 𝑃∧(𝑃∨𝑄)≡𝑃P∧(P∨Q)≡P。

P	Q	𝑃∧𝑄P∧Q	𝑃∨(𝑃∧𝑄)P∨(P∧Q)	𝑃∨𝑄P∨Q	𝑃∧(𝑃∨𝑄)P∧(P∨Q)
T	T	T	T	T	T
T	F	F	T	T	T
F	T	F	F	T	F
F	F	F	F	F	F

从表中可以看到，吸收律成立。

等价置换

定义1-4.3 如果X是合式公式A的一部分，且X本身也是一个合式公式，则称X为公式A的子公式。

定理1-4.1 设X是合式公式A的子公式，若 𝑋≡𝑌X≡Y，如果将A中的X用Y来置换，所得到的公式B与公式A等价，即 𝐴≡𝐵A≡B。

证明 因为在相应变元的任一种指派情况下，X与Y的真值相同，故以Y取代X后，公式B与公式A在相应的指派情况下其真值亦必相同，故 𝐴≡𝐵A≡B。

满足定理1-4.1条件的置换称为等价置换（等价代换）。

例题7 证明 𝑄→(𝑃∨(𝑃∧𝑄))≡𝑄→𝑃Q→(P∨(P∧Q))≡Q→P。

Q	P	𝑃∧𝑄P∧Q	𝑃∨(𝑃∧𝑄)P∨(P∧Q)	𝑄→(𝑃∨(𝑃∧𝑄))Q→(P∨(P∧Q))	𝑄→𝑃Q→P
T	T	T	T	T	T
T	F	F	F	F	F
F	T	F	T	T	T
F	F	F	F	T	T

从表中可以看到， 𝑄→(𝑃∨(𝑃∧𝑄))Q→(P∨(P∧Q)) 与 𝑄→𝑃Q→P 的真值相同，故命题得证。

通过上述命题公式的等价关系，我们可以利用定理1-4.1，在证明一些更为复杂的等为复杂的等价公式时，进行等价置换，使得证明更加简洁明了。现举例说明如下：

例题8 证明 (𝑃∧𝑄)∨(𝑃∧¬𝑄)≡𝑃(P∧Q)∨(P∧¬Q)≡P。

证明：

1. 原式： (𝑃∧𝑄)∨(𝑃∧¬𝑄)(P∧Q)∨(P∧¬Q)
2. 根据分配律：𝑃∧(𝑄∨¬𝑄)P∧(Q∨¬Q)
3. 𝑄∨¬𝑄≡𝑇Q∨¬Q≡T
4. 𝑃∧𝑇≡𝑃P∧T≡P

因此，(𝑃∧𝑄)∨(𝑃∧¬𝑄)≡𝑃(P∧Q)∨(P∧¬Q)≡P，命题得证。

例题9 证明 𝑃→(𝑄→𝑅)≡𝑄→(𝑃→𝑅)P→(Q→R)≡Q→(P→R)。

证明：

1. 原式： 𝑃→(𝑄→𝑅)P→(Q→R)
2. 条件转化：¬𝑃∨(¬𝑄∨𝑅)¬P∨(¬Q∨R)
3. 结合律：(¬𝑃∨¬𝑄)∨𝑅(¬P∨¬Q)∨R
4. 条件转化：¬𝑄→(¬𝑃∨𝑅)¬Q→(¬P∨R)
5. 条件转化：¬𝑄→(𝑃→𝑅)¬Q→(P→R)
6. 逆反律：𝑄→(𝑃→𝑅)Q→(P→R)

因此，𝑃→(𝑄→𝑅)≡𝑄→(𝑃→𝑅)P→(Q→R)≡Q→(P→R)，命题得证。

例题10 证明 ¬(𝑃→𝑄)≡𝑃∧¬𝑄¬(P→Q)≡P∧¬Q。

证明：

1. 原式： ¬(𝑃→𝑄)¬(P→Q)
2. 条件转化：¬(¬𝑃∨𝑄)¬(¬P∨Q)
3. 德摩根律：𝑃∧¬𝑄P∧¬Q

因此，¬(𝑃→𝑄)≡𝑃∧¬𝑄¬(P→Q)≡P∧¬Q，命题得证。

习题

1. 求下列各复合命题的真值表。

   • (a) 𝑃→(𝑄∨𝑅)P→(Q∨R)
   • (b) (𝑃∧𝑅)∨(𝑃→𝑄)(P∧R)∨(P→Q)
   • (c) (𝑃∨𝑄)≡(𝑄∨𝑃)(P∨Q)≡(Q∨P)
   • (d) (𝑃∨¬𝑄)∧𝑅(P∨¬Q)∧R
   • (e) (𝑃→(𝑄→𝑅))≡((𝑃→𝑄)→(𝑃→𝑅))(P→(Q→R))≡((P→Q)→(P→R))

2. 试求下列各命题的真值表并解释其结果。

   • (a) ¬(𝑃∧𝑄)¬(P∧Q)
   • (b) 𝑃→𝑄P→Q
   • (c) 𝑃↔𝑄P↔Q
   • (d) 𝑃∧¬𝑄P∧¬Q

3. 证明下列等价式：

   • (a) 𝐴∧(𝐵→𝐴)≡¬𝐴→(𝐴→¬𝐵)A∧(B→A)≡¬A→(A→¬B)
   • (b) 𝐴≡𝐵≡(𝐴∨𝐵)∧(¬𝐴∨¬𝐵)A≡B≡(A∨B)∧(¬A∨¬B)
   • (c) (𝐴→𝐵)≡¬𝐴∨𝐵(A→B)≡¬A∨B
   • (d) ¬(𝐴≡𝐵)≡𝐴∧¬𝐵∨¬𝐴∧𝐵¬(A≡B)≡A∧¬B∨¬A∧B
   • (e) (𝐴∧𝐵→𝐶)≡(𝐴→(𝐵→𝐶))(A∧B→C)≡(A→(B→C))
   • (f) 𝐴≡(𝐵∨𝐶)≡(𝐴∧¬𝐵)∨𝐶A≡(B∨C)≡(A∧¬B)∨C
   • (g) (𝐴→𝐷)∧(𝐵→𝐷)≡(𝐴∨𝐵)→𝐷(A→D)∧(B→D)≡(A∨B)→D
   • (h) (𝐴∧𝐵)→𝐶)≡(𝐴→(𝐵→𝐶))(A∧B)→C)≡(A→(B→C))

4. 化简以下各式：

   • (a) (𝐴→𝐵)≡(¬𝐵→¬𝐴)∧𝐶(A→B)≡(¬B→¬A)∧C
   • (b) 𝐴∨(¬𝐴∨(𝐵∧𝐶))A∨(¬A∨(B∧C))
   • (c) (𝐴∧𝐵∧𝐶)∨(¬𝐴∧𝐵∧𝐶)(A∧B∧C)∨(¬A∧B∧C)

5. 如果 𝐴∨𝐶≡𝐵∨𝐶A∨C≡B∨C，是否有 𝐴≡𝐵A≡B？

   • 如果 𝐴∧𝐶≡𝐵∧𝐶A∧C≡B∧C，是否有 𝐴≡𝐵A≡B？
   • 如果 ¬𝐴≡¬𝐵¬A≡¬B，是否有 𝐴≡𝐵A≡B？

通过上述例题和习题的训练，可以加深对命题逻辑中真值表与等价公式的理解和应用。