2.7 合并排序

---

博主介绍:夏驰和徐策

所属专栏:算法设计与分析

上期回顾：2.6 棋盘覆盖

---

合并排序算法是用分治策咯实现对 n 个元素进行排序的算法，其基本思想是：将待排序

元素分成大小大致相同的两个子集合，分别对两个子集合进行排序，最终将排好序的子集合

合并成要求的排好序的集合。合并排序算法可递归地描述如下：

template<class Type>
void MergeSort(Type a[],int left,int right)
{
    if(left<right)//至少两个元素
        {
            int i=(left+right)/2;//取中点              
            MergeSort(a,left,i);
            MergeSort(a,i+1,right);
            Merge(a,b,left,i,right);//合并到数组b
            Copy(a,b,left,right);//复制回数组a
        }
}

其中，算法 Merge 合并两个排好序的数组段到一个新的数组b中，然后由 Copy将合并后的数组段再复制回数组a中。Merge 和 Copy 显然可在 O（n时间内完成，因此合并排序算法对n个元素进行排序，在最坏情况下所需的计算时间 T(n)满足

[O(1)

T(n) =

(27 (n / 2) + 0(n)

n≤1

n>1

解此递归方程可得 7n=0(nlogn)。由于排序问题的计算时间下界为 S2(nlogn，故合并排

序算法是一个渐近最优算法。

对于算法 Mergesort，还可以从多方面对它进行改进。例如，从分治策路的机制入手，容

易消除算法中的递归。事实上，算法Mergesort 的递归过程只是将待排序集合

一分为二，直至

待排序集合只剩下一个元素为止，然后不断合并两个排好序的数组段。按此机制，可以先将数

组a中相邻元素两两配对。用合并算法将它们排序，构成 n/2 组长度为2的排好序的子数组段，

再将它们排序成长度为4 的排好序的子数组段。如此继续下去，直至整个数组排好序

按此思想，消去递归后的合并排序算法可描述如下：

template<class type>
void MergeSort(Type a[],int n)
{
    Type *b=new Type [n];
    int s=1;
    while(s<n)
    {
        MeragePass(a,b,s,n);//合并到数组b
        s+=s;
        MergePass(b,a,s,n);//合并到数组a
        s+=s;
    }
}

其中，两数 MergePassO用于合并排好序的相邻数组段。具体的合并算法由 Merge0函数来实现。注意，定义关于类型为Type 的元素的比较运算“＜=”。特别地，如果 Type 是自定义的：则必须重载运算 “<=”

template<class Type>
void mergepass(Type x[],Type y[],int s,int n)
{
    int i=0;
    while(i<=n-2*s)
        {
            Merge(x,y,i,i+s-1,i+2*s-1);
            i=i+2*s;       
        }
    if(i+2<n)
        {
            Merge(x,y,i,i+s-1,n-1);
        }else {
                for(int j=i;j<=n-1;j++)
                    {
                        y[j]=x[j];
                    }
              }
tempalte<class Type>
{
    void Merge(Type c[],Type d[],int l,int m,int r)
                {
                    int i=1,j=m+1,k=l;
                    while((i<=m)&&(j<=r))
                        {
                            if(c[i]<=c[j])
                                {
                                    d[k++]=c[i++];
                                }else{
                                        for(int q=j;q<=r;q++)
                                            {
                                                d[k++]=c[q];    
                                            }
                                      }
                        }

                }
}
}

自然合并排序是上述合并排序算法MergeSort的一个变形。在上述合并排序算法,第一步合我相卻长没为1的子数红段，这起街我很奶，的一款湖教是已排好序的。事实上，子初始给定的效组a，延路存任我不很酸大手 1的已百然我产的于数组段。例如，者数組a中死發为什83.7.1,5,0.21则自然排好牌的子数到段有？85 3.71、(1, 5.01利112t6用工认对数红a的线性子描就足以找出所有这业我月的子致组段。然后特相邻的排好序的子数组髮两两合井，构成更大的排好序的于数红段。对上面的例子，经一次合并后可得到2个合并后的子数组段：3,4,7,84和(，2,5.6-。*续合并相邻排好序的子数组段，直至整个数组己排好序。上面这两个数组段再合并后就得到41,2,3,4,5,6,7,8)。上述思想就是自然合并排序算法的基本恩想。在通常情況下，按此方式进行合并排序所需的合并次数较少。例如，对于所给的，元素数组己排好序的极端情况，自然合并排序算法不需要执行合并步，而算法 MergeSort 需要执行「ogn1 次合并。因此，在这种情况下，自然合并排序算法需要C(D时间，而算法 MergeSort 需要 O(nlogn时间。

我的理解部分：

归并排序的步骤：

给定一个 N 个项目的数组，归并排序将：

1. 将每对单个元素（默认情况下，已排序）归并为2个元素的有序数组，

2. 将2个元素的每对有序数组归并成4个元素的有序数组，重复这个过程......，

3. 最后一步：归并2个N / 2元素的排序数组（为了简化讨论，我们假设N是偶数）以获得完全排序的N个元素数组。

这只是一般的想法，在我们可以讨论归并排序的真正形式之前，我们需要更多的细节。

我们首先从归并排序算法的最重要的子程序 -- O(N) 归并来剖析这个归并排序算法。

给定两个大小分别为 N1 和 N2 的排序数组 A 和 B，我们可以在O(N) 时间内将它们有效地归并成一个大小为 N = N1 + N2的组合排序数组。

这是通过简单地比较两个数组的首项并始终取两个中较小的一个来实现的。 但是，这个简单但快速的O(N)合并子程序将需要额外的数组来正确合并。

代码及其中的疑问

void merge(int a[], int low, int mid, int high) {
  // subarray1 = a[low..mid], subarray2 = a[mid+1..high], both sorted
  int N = high-low+1;
  int b[N]; // 讨论: 为什么我们需要一个临时的数组 b?
  int left = low, right = mid+1, bIdx = 0;
  while (left <= mid && right <= high) // 归并
    b[bIdx++] = (a[left] <= a[right]) ? a[left++] : a[right++];
  while (left <= mid) b[bIdx++] = a[left++]; // leftover, if any
  while (right <= high) b[bIdx++] = a[right++]; // leftover, if any
  for (int k = 0; k < N; k++) a[low+k] = b[k]; // copy back
}

归并排序代码动图：

简单：

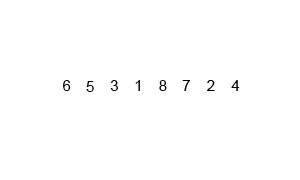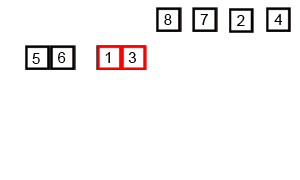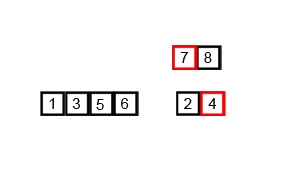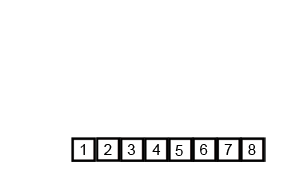
用树形图举个例子：

动态图：

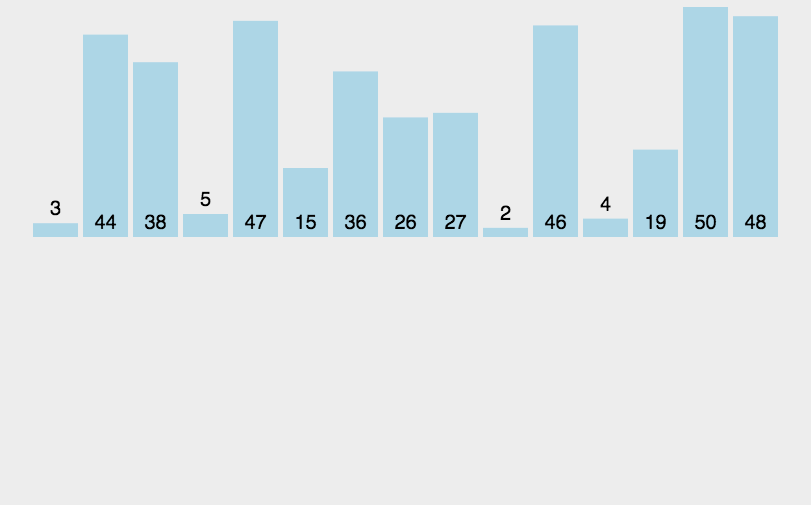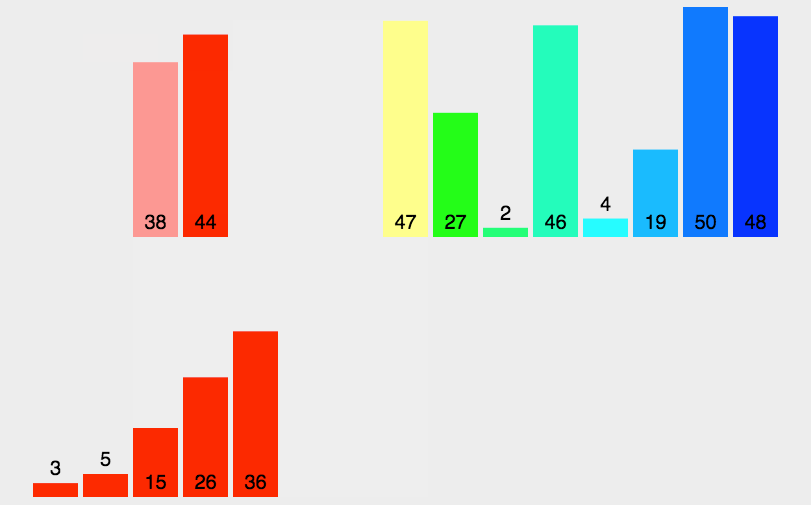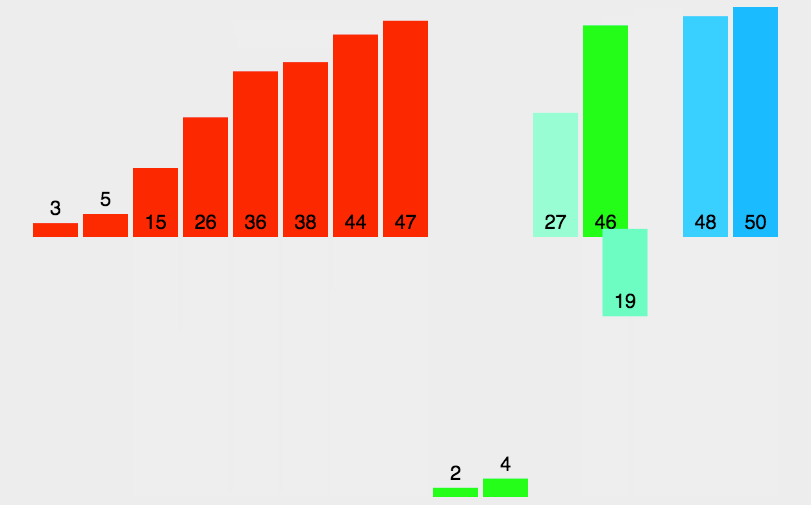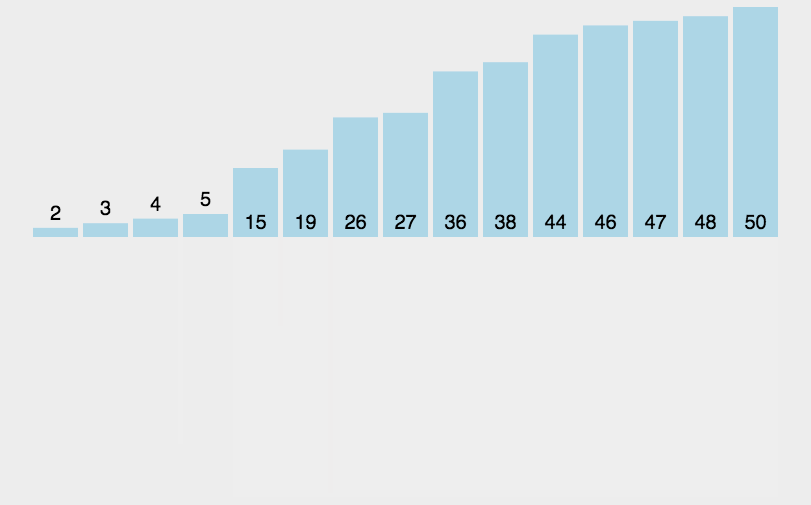
抽象图：