1.3 数值运算中误差传播规律简析

在数值运算中,参加运算的数若有误差，必然会影响到计算结果的准确性．今以二元函数为例,通过泰勒(Taylor) 展开来分析误差的传播规律。

设x1*,x2*分别是x1,x2的近似值。在实际计算时,常用y*=f(x1*,x2*)作为函数值y=f(x1,x2)的近似值。利用函数f(x1,x2)的近似值,在点(x1*,x2*）处的泰勒展开式，可方便地估计近似值,y*的绝对误差与相对误差。例如，当x1*与x2*的误差都较小时,y*的绝对误差。

绝对误差与微分之间的关系：

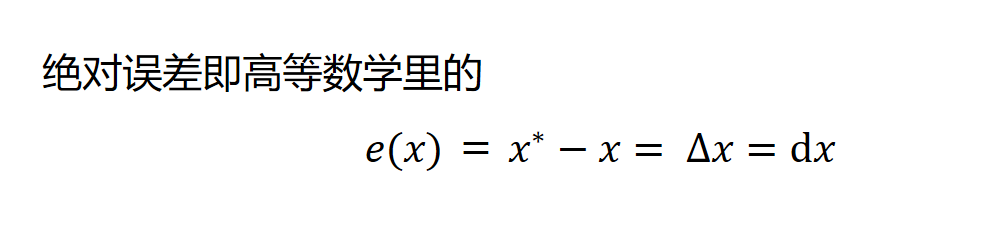
绝对误差的运算：

反思：

对偏导数几乎已经忘完了，现在的首要任务就是解决高数里面各个薄弱的几个模块。