1. 幂函数
(1)定义:形如,
的函数。
(2)常见幂函数:,
;
,
,
;
,
,
。
(3)图像:
| | | | | |
| 图像 | 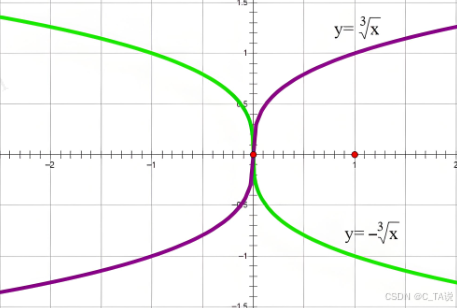 | 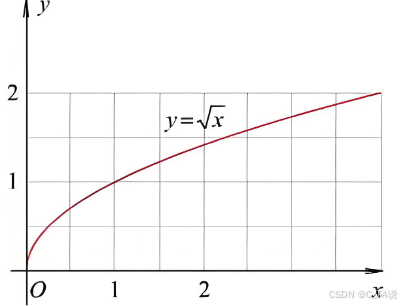 | 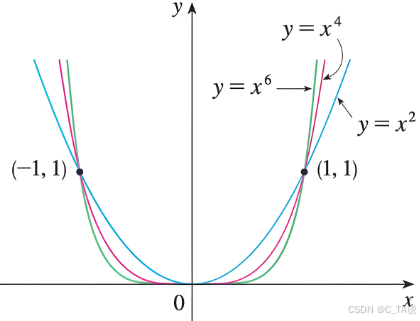 | 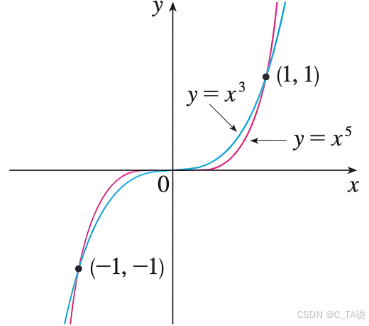 |
(4)运算法则:
①:同底数幂相乘,底数不变,指数相加。 ②:同底数幂相除,底数不变,指数相减。
③:同指数幂相乘,指数不变,底数相乘。 ④:同指数幂相除,指数不变,底数相除。
⑤:幂的乘方,底数不变,指数相乘,即。 ⑥:分式乘方,分子分母分别乘方,指数不变。
⑦:积的乘方,等于把积的每一个因式分别乘方,再把所得的值相乘,即。 ⑧:
。
备注:①:零指数幂:
。 ②:负指数幂:
。
2. 指数函数
(1)定义:形如,
且
≠ 1,
的函数。
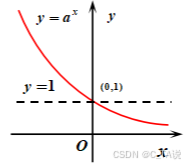
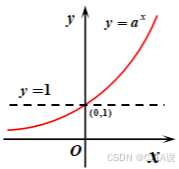
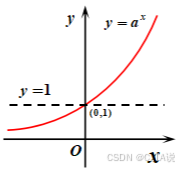
(2)图像:
| | | | |
| 图 像 |
|
|
|
| 定义域 | | | |
| 值 域 | | | |
| 过 点 | | | |
| 趋 势 | 底越小,图像越靠近坐标轴 | 底越大,图像越靠近坐标轴 | 上图: |
(3)运算法则:
①:同底数幂相乘,底数不变,指数相加。 ②:同底数幂相除,底数不变,指数相减。
③:同指数幂相乘,指数不变,底数相乘。 ④:同指数幂相除,指数不变,底数相除。
⑤:幂的乘方,底数不变,指数相乘,即。 ⑥:分式乘方,分子分母分别乘方,指数不变。
⑦:积的乘方,等于把积的每一个因式分别乘方,再把所得的值相乘,即。
⑧:。 ⑨:
.
备注:①:零指数幂:
。 ②:负指数幂:
。
3. 对数函数
(1)定义:形如,
且
≠ 1,
的函数。
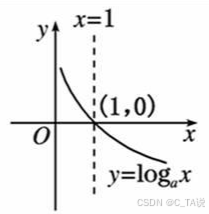
(2)图像:
| | | | |
| 图 像 |
|
|
|
| 定义域 | | | |
| 值 域 | | | |
| 过 点 | | | |
| 趋 势 | 底越小,图像越靠近坐标轴 | 底越大,图像越靠近坐标轴 | 上图: |
(3)运算法则:
①: ②:
③:
④: ⑤:
⑥:
⑦: ⑧:
4. 三角函数
(1)常用关系式:
①: ②:
③: ④:
⑤: ⑥:
⑦: ⑧:
(2)常见三角函数:,
,
,
,
,
。
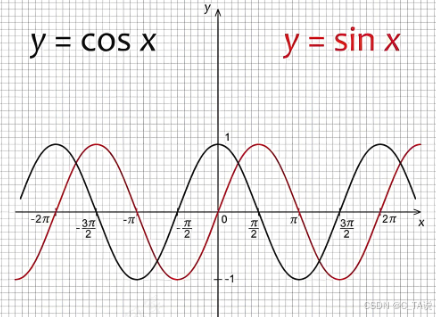
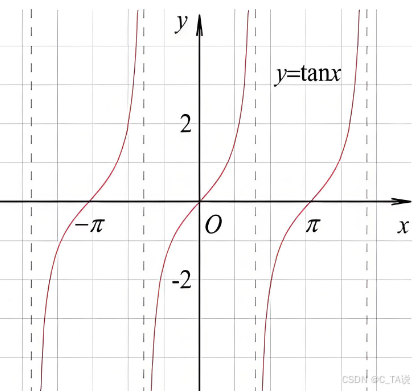
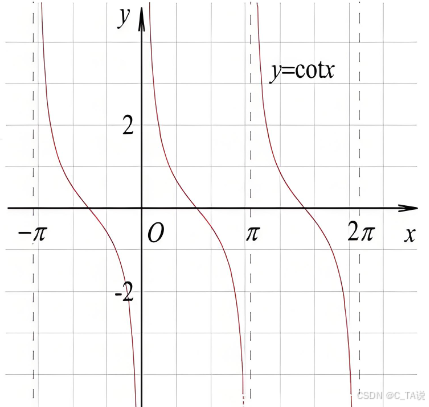
(3)图像:
| | | | | | ||
| 图像 |
|
|
| 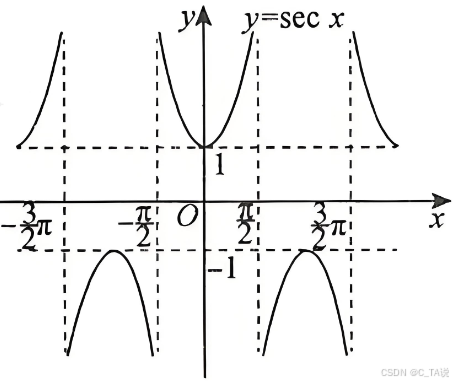 | 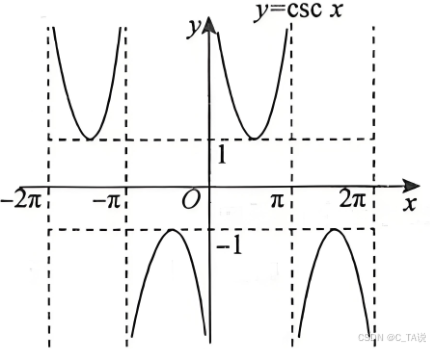 | |
| 定义域 | | | { | { | { | { |
| 值域 | [-1,1] | [-1,1] | | | (- | (- |
| 周期 | | | | | | |
5. 反三角函数
(1)反三角函数:①:反三角函数属于反函数,其直接函数是三角函数;②:反三角函数与三角函数关于对称。
(2)常见反三角函数:,
,
,
。
(3)图像:
| | | |||
| 图像 | 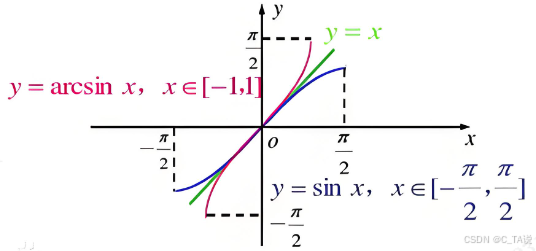 | 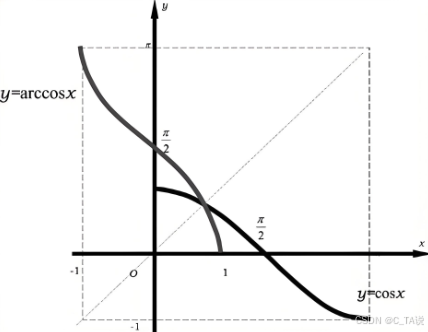 | 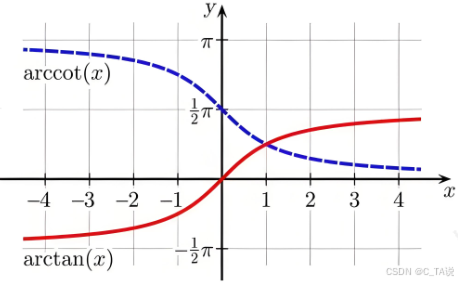 | |
| 定义域 | [-1,1] | [-1,1] | | |
| 值域 | [- | [0, | (- | (0, |
| 周期 | 非周期函数 | 非周期函数 | 非周期函数 | 非周期函数 |
(4)反三角函数求解:
①:求解,其实就是求解
。 ②:求解
,其实就是求解
。
③:求解,其实就是求解
。 ④:求解
,其实就是求解
。






















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








