1. 二阶三阶行列式
1.1 行列式的引入
定义一个二元一次方程组:
(1)求解 x 消 y:将方程(1)两边同时乘以9,方程(2)两边同时乘以4,可得:
解得:
(2)求解 y 消 x:将方程(1)两边同时乘以7,方程(2)两边同时乘以3,可得:
解得:
(3)观察x,y的结果,为了使结果表达的更清晰些,故定义了一个规则,规则如下:
小贴士:行列式用D表示,即英文Determinant的首字母。
1.2 二阶行列式
(1)定义:由 2行 2列 4个元素构成的式子。
(2)表示:.
备注:
1. 行列式计算结果为一个数,即结果为标量。
2. 行列式中某元素用
表示,代表第 i 行,第 j 列的元素。
3. 使用行列式的定义计算行列式的值时,几阶行列式则每一项就有几个元素相乘。
4. 一阶行列式:
,“| |”非绝对值。
1.3 三阶行列式
(1)定义:由 3行 3列 9个元素构成的式子。
(2)表示方法:
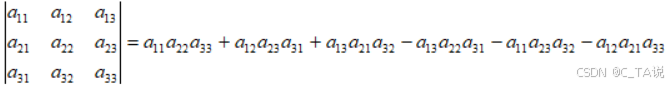
(3)常见特殊行列式:
主对角线-上三角行列式: 主对角线-下三角行列式:
主对角线-对角行列式:
副对角线-上三角行列式: 副对角线-下三角行列式:
副对角线-对角行列式:
2. n阶行列式
2.1 基础知识
(1)排列
1)定义:由1,2,3...n组成的有序数列,则称为一个n级排列。
2)排列数:n级排列的排列个数。n级排列的排列数为n! 。
备注:n级标准排列:从1到n按照递增顺序排列的n级排列。
(2)逆序
1)定义:在一个n级排列中,如果较大的数排在了较小的数
的前面,则称
与
构成了一个
逆序。
2)逆序数:在一个n级排列中逆序的个数。记作:。
备注:n级标准排列的逆序数为0。
(3)排列的奇偶性
1)奇排列:在一个n级排列中,若逆序数为奇数,则称该排列为奇排列。
2)偶排列:在一个n级排列中,若逆序数为偶数,则称该排列为偶排列。
备注:n级标准排列是偶排列。
(4)对换
定义:在一个n级排列中,任意互换两个数的位置,其余数的位置不变,则形成一个新的n级排
列,此操作称之为对换。
备注:
1. 一个n级排列每对换一次,奇偶性发生一次改变。
2. n级排列的排列数为n!,其中奇排列的个数与偶排列的个数相等,为n!/2(n≥2)。
2.2 n阶行列式
(1)定义:由 n行 n列 个元素构成的式子,简记为
。
(2)表示方法:
1)n阶行列式按行展开:
备注:
1. 一共有n!项做和;
2. 每一项中包含了n个元素,这n个元素的行标取标准排列,列标取排列的所有可能;
3. 每一项的正负由这n个元素的列标排列的奇偶性决定;
4. 确保每一项取自不同行不同列的元素相乘。
小贴士:明确按行展开后,那么第一行取啥昵,第二行取啥昵,要保证是不同行不同列呦!
2)n阶行列式按列展开:
备注:
1. 一共有n!项做和;
2. 每一项中包含了n个元素,这n个元素的列标取标准排列,行标取排列的所有可能;
3. 每一项的正负由元素的行标排列的奇偶性决定;
4. 确保每一项取自不同行不同列的元素相乘。
小贴士:明确按列展开后,那么第一列取啥昵,第二列取啥昵,要保证是不同行不同列呦!
(3)常见特殊行列式:
主对角线-上、下三角行列式:
主对角线-对角行列式:
副对角线-上、下三角行列式:
副对角线-对角行列式:
小贴士:若行列式的某行或某列的元素全为0,那么此行列式的值为0。
3. 行列式的性质
引:转置行列式:就是把行列式相对应的行与列进行互换,记作
。
(1)行列式与转置行列式的值相等,即行列式的行列互换,其值不变。
(2)交换行列式的两行(两列),行列式的值符号改变。
推论:若行列式中有两行(两列)对应的元素相等或成比例,则行列式的值为0。
(3)用数 k 去乘行列式的某一行(列)的所有元素,等于用数 k 去乘此行列式。
推论:若行列式的所有行(列)均有公因子 k,则 k 外提 n 次,提出去的 k 乘到一起。
(4)若行列式的某一行(列)的各元素都是两个数之和,则此行列式等于两个行列式之和,这两
个行列式分别以这两个数之一作为所在行(列)对应位置的元素,其他位置的元素与原行列
式相同。
注意:每次仅拆分一行(一列),多次拆分最好分开操作。
(5)将行列式的某一行(列)的所有元素乘以同一数k后加到另一行(列)对应位置的元素上,则
行列式的值不变。
注意:使用时按照顺序执行,不要反其道而行之。
小贴士:
反对称行列式:n阶行列式中的元素满足
。
1. 主对角线元素全为0。
2. 以主对角线为轴,上下元素互为相反数。
3. 奇数阶反对称行列式的值为0。
4. 行列式按一行(列)展开
4.1 余子式与代数余子式
(1)余子式:在n(n>1)阶行列式中,把元素所在的行与列去掉,剩余的元素按照原来的相对位
置,重新组合成新的n-1阶行列式,那么新的n-1阶行列式称为该元素的余子式,记作。
(2)代数余子式:把称为该元素的代数余子式,记作
。
备注:
=
。
4.2 行列式按一行(列)展开
(1)定义:n阶行列式的值等于它的任意一行(列)的所有元素与其对应的代数余子式的乘积的和。
(2)方法:先按照行列式的性质尽可能多的化0,然后再按照0比较多的行(列)展开。
(3)意义:把高阶行列式化为低阶行列式来计算。
4.3 异乘变零原理
定义:在n(n>1)阶行列式中,某一行(列)的所有元素与另一行(列)中对应元素的代数余子式
的乘积的和为0。
5. 行列式按多行(列)展开
5.1 k阶余子式与代数余子式
(1)k阶子式:在n阶行列式中,任意选取k行k列(1≤k≤n),位于行列交叉点的个元素,按照原来
的相对位置,重新组合成新的k阶行列式,那么新的k阶行列式称为原行列式的一个k阶子式。
(2)k阶余子式:在n阶行列式中,把k阶子式所在行与列去掉,剩余的元素按照原来的相对位置,
重新组合成新的n-k阶行列式,那么新的n-k阶行列式就称为该k阶子式的余子式,记作。
(3)k阶代数余子式:把(
表示k阶子式是由哪几行哪几列组成的)称为
该k阶子式的代数余子式,记作。
备注:
5.2 行列式按多行(列)展开
(1)定义:在n阶行列式中,任意选取k行(列)(1≤k≤n-1),则由这k行(列)元素所组成的所有
k阶子式与它们对应的代数余子式的乘积的和,就是n阶行列式的值。
(2)方法:行(列)的选取原则是要保证所组成的k阶子式可用于计算的数量最少。
(3)意义:把高阶行列式化为低阶行列式来计算。
5.3 常用特殊行列式
主对角线-上、下三角行列式: 主对角线-对角行列式:
副对角线-上、下三角行列式:
副对角线-对角行列式:
备注:A是m阶行列式,B是n阶行列式,O是全为0的行列式。
6. 克拉默法则
(1)含有 n个方程 n个未知数的 n元非齐次线性方程组:
当系数行列式D ≠ 0时(系数行列式:由未知数的系数按照其相对位置所构成的行列式),
则方程组有唯一解,且唯一解为:
其中(行列式是系数行列式
中第
列元素换为方程组右端的常数项所得):
备注:克拉默法则使用的前提条件:
1. 方程的个数等于未知数的个数。
2. 系数行列式不等于0。
(2)含有 n个方程 n个未知数的 n元齐次线性方程组:
当系数行列式D ≠ 0时(系数行列式:由未知数的系数按照其相对位置所构成的行列式),
则方程组只有零解(零解不是无解,解是0)。
备注:克拉默法则使用的前提条件:
1. 方程的个数等于未知数的个数。
2. 系数行列式不等于0。
(3)重要知识点:
对于方程组的个数等于未知数的个数的齐次线性方程组而言:
1)齐次线性方程组有非零解的充分必要条件是D = 0。
2)齐次线性方程组只有零解的充分必要条件是D ≠ 0。
小贴士:
(1)在n阶行列式中,若行(列)的和相等,则每列的所有元素加到第一列(行)上。
(2)对于爪型行列式(箭头形状),则每列(除第一列外)处理后都加到第一列上,使第一
列元素变为0(第一行除外)。
(3)范德蒙德行列式:运算时仅看第二行元素就行,逐一作差相乘。





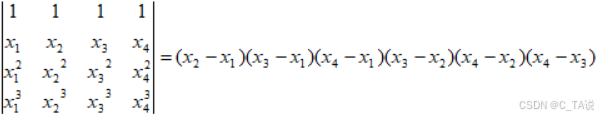
















 4492
4492

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








