高等数学笔记-乐经良老师
第二章 极限与连续
第四节 函数的极限
一、函数极限的定义
01 自变量趋于无穷大时函数的极限
(1) x→+∞x \rightarrow+\inftyx→+∞ 的情况
-
x→+∞x \rightarrow+\inftyx→+∞
-
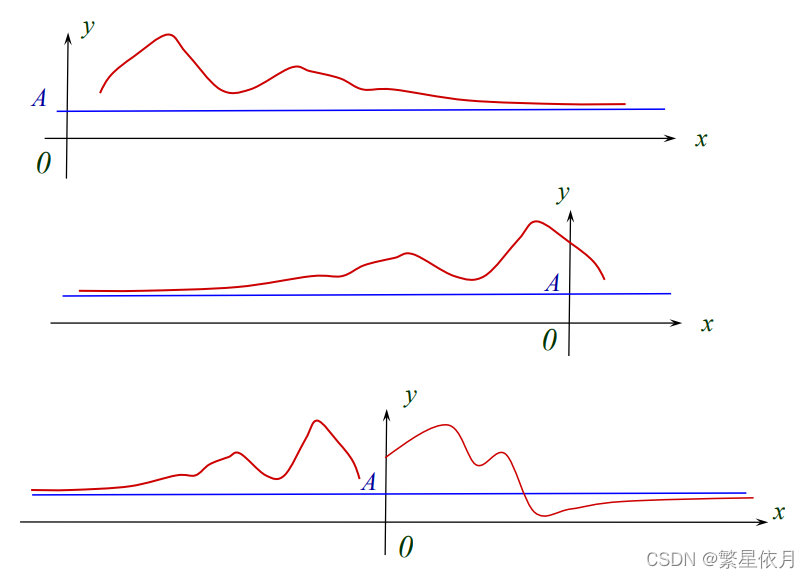
设 f(x)f(x)f(x) 定义在 [a,+∞),∃A∈R,∀ε>0[a,+\infty), \exists A \in \mathbf{R}, \forall \varepsilon>0[a,+∞),∃A∈R,∀ε>0, ∃X>a\exists X>a∃X>a, 当 x>Xx>Xx>X,
∣f(x)−A∣<ε |f(x)-A|<\varepsilon ∣f(x)−A∣<ε
称当 xxx 趋于正无穷时, f(x)f(x)f(x) 的极限为 AAA, 或收敛于 AAA 记为
limx→+∞f(x)=A 或 f(x)→A,(x→+∞) \lim _{x \rightarrow+\infty} f(x)=A \text { 或 } f(x) \rightarrow A,(x \rightarrow+\infty) x→+∞limf(x)=A 或 f(x)→A,(x→+∞) -
注意将此情况与数列极限比较
-
-
x→−∞x \rightarrow-\inftyx→−∞
- 自己写
(2) x→∞x \rightarrow \inftyx→∞ 的情况
-
设 f(x)f(x)f(x) 定义在 ∣x∣>a,∃A∈R,∀ε>0|x|>a, \exists A \in \mathbf{R}, \forall \varepsilon>0∣x∣>a,∃A∈R,∀ε>0, ∃X>a\exists X>a∃X>a, 当 ∣x∣>X|x|>X∣x∣>X,
∣f(x)−A∣<ε |f(x)-A|<\varepsilon ∣f(x)−A∣<ε
称当 xxx 趋于无穷时, f(x)f(x)f(x) 的极限为 AAA, 或收敛于 AAA 记为
limx→∞f(x)=A 或 f(x)→A,(x→∞) \lim _{x \rightarrow \infty} f(x)=A \text { 或 } f(x) \rightarrow A,(x \rightarrow \infty) x→∞limf(x)=A 或 f(x)→A,(x→∞) -
推论
- limn→∞f(x)=A⇔limn→+∞f(x)=A且limn→−∞f(x)=A\lim \limits_{n \rightarrow \infty} f(x)=A \quad \Leftrightarrow \quad \lim \limits_{n \rightarrow +\infty} f(x)=A \text{且} \lim \limits_{n \rightarrow -\infty} f(x)=An→∞limf(x)=A⇔n→+∞limf(x)=A且n→−∞limf(x)=A
-
x→±∞x \rightarrow±\inftyx→±∞和∞\infty∞的极限
-
02 自变量趋于有限值时函数的极限
(1) x→ax \rightarrow ax→a 的情况
-
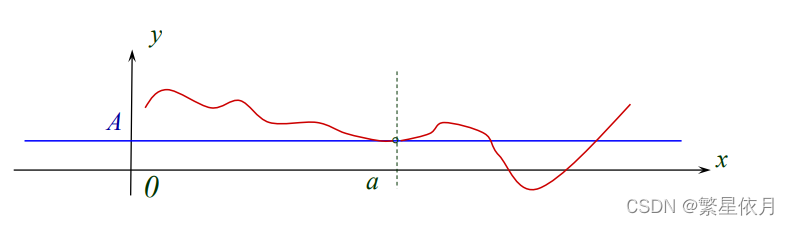
设 f(x)f(x)f(x) 定义在 aaa 的去心邻域, 若存在实数 AAA, ∀ε>0,∃δ>0\forall \varepsilon>0, \exists \delta>0∀ε>0,∃δ>0, 当 0<∣x−a∣<δ0<|x-a|<\delta0<∣x−a∣<δ,
∣f(x)−A∣<ε |f(x)-A|<\varepsilon ∣f(x)−A∣<ε
称当 xxx 趋于 aaa 时, f(x)f(x)f(x) 的极限为 AAA, 或收敛于 AAA 记为
limx→af(x)=A 或 f(x)→A,(x→a) \lim _{x \rightarrow a} f(x)=A \quad \text { 或 } \quad f(x) \rightarrow A,(x \rightarrow a) x→alimf(x)=A 或 f(x)→A,(x→a) -
定义在去心邻域说明 aaa 点的定义是否存在我们并不关心
-
从定义知, 此极限与 f(x)f(x)f(x) 在 aaa 点的定义无关, 也与 f(x)f(x)f(x) 在 aaa 的邻域外的值无关
-
x→ax \rightarrow ax→a 时的极限是一种双侧极限
(2) x→a+x \rightarrow a^{+}x→a+ 的情况(单侧极限)
-
设 η>0,f(x)\eta>0, f(x)η>0,f(x) 定义在 (a,a+η)(a, a+\eta)(a,a+η), 若存在实数 AAA
∀ε>0,∃δ>0, 当 0<x−a<δ,∣f(x)−A∣<ε\forall \varepsilon>0, \exists \delta>0, \text { 当 } 0<x-a<\delta, \\ |f(x)-A|<\varepsilon∀ε>0,∃δ>0, 当 0<x−a<δ,∣f(x)−A∣<ε
称 f(x)f(x)f(x) 在 aaa 点的右极限为 AAA, 记为
limx→a+f(x)=A或f(x)→A,(x→a+)或f(a+0)=A\lim \limits_{x \rightarrow a^{+}} f(x)=A \enspace或\enspace f(x) \rightarrow A,\left(x \rightarrow a^{+}\right)\enspace或\enspace f(a+0)=Ax→a+limf(x)=A或f(x)→A,(x→a+)或f(a+0)=A
-
考虑 x→a−(x \rightarrow a^{-}(x→a−(或 a−0)a-0)a−0) 的情况
-
显然有,命题
- limx→af(x)=A⇔limx→a+f(x)=A 且 limx→a−f(x)=A\lim \limits_{x \rightarrow a} f(x)=A \quad \Leftrightarrow \quad \lim \limits_{x \rightarrow a^{+}} f(x)=A \text { 且 } \lim \limits_{x \rightarrow a^{-}} f(x)=Ax→alimf(x)=A⇔





 本文详细介绍了函数极限的定义,包括自变量趋近正负无穷大、有限值时的情况,以及无穷小与无穷大的概念。讲解了极限的唯一性、局部有界性和保号性等性质,并探讨了运算法则和判别法。涉及的重要极限如三角函数和指数函数极限,以及无穷小比较和阶的分析。
本文详细介绍了函数极限的定义,包括自变量趋近正负无穷大、有限值时的情况,以及无穷小与无穷大的概念。讲解了极限的唯一性、局部有界性和保号性等性质,并探讨了运算法则和判别法。涉及的重要极限如三角函数和指数函数极限,以及无穷小比较和阶的分析。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 868
868










