高等数学笔记-乐经良老师-第九章-重积分

已于 2024-05-02 14:31:26 修改 · 1.7k 阅读

文章标签：

于 2022-05-17 23:53:22 首次发布

本文详细介绍了重积分的概念，包括二重积分和三重积分，并通过实例展示了如何计算平面薄板的质量、曲顶柱体的体积以及在直角坐标系和极坐标系下的计算方法。此外，讨论了重积分在求解曲面面积、质心和转动惯量等实际问题中的应用。最后，提到了变量代换在三重积分中的运用，以及柱面坐标和球面坐标系下的积分计算。

高等数学笔记-乐经良老师

第九章重积分

第一节二重积分的概念和性质

一、典型例子

01 平面薄板的质量

平面薄板位于 $x y$ 平面区域 $D$ ，其面密度为 $μ (x, y)$ 如何求其质量？

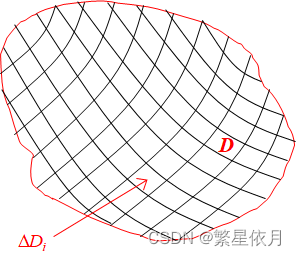
在这里插入图片描述

类似一元的处理方法，采用：

(1) 分割

将 $D$ 任意划分成 $n$ 个小区域 $,ΔDn,ΔDi\Delta D_{1}, \Delta D_{2}, \cdots, \Delta D_{n}, \Delta D_{i}$ 的面积记为 $,n)\Delta \sigma_{i},(i=1,2, \cdots, n)$

(2) 作和

在小区域分得很小时，近似认为质量均匀，任取 $(ξi,ηi)∈ΔDi\left(\xi_{i}, \eta_{i}\right) \in \Delta D_{i}$ ，薄板的质量近似地表达为
$m=\sum_{i=1}^{n} \Delta m_{i} \approx \sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}$
(3) 取极限

记 $di}\lambda=\max \limits_{1 \leq 1 \leq n}\left\{d_{i}\right\}$ ，( $d_{i}$ 是小区域 $ΔDi\Delta D_{i}$ 的直径 ) 那么若
$m=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}$
存在，就给出了薄板的质量。

02 曲顶柱体的体积

柱体的侧面是母线垂直 $x y$ 平面的柱面，顶面为曲面 $S : z = f (x, y)$ ，

底面是 $x y$ 平面上区域 $D$ ，如何求此曲顶柱体的体积？

在这里插入图片描述

(1) 分割

用曲线将 $D$ 分成小区域 $,ΔDn\Delta D_{1}, \Delta D_{2}, \cdots, \Delta D_{n}$ ，而 $ΔDi\Delta D_{i}$ 的面积记为 $Δσi\Delta \sigma_{i}$

(2) 求和

区域分得很小时，用柱体来近似小曲顶柱体的体积，任取 $(ξi,ηi)∈ΔDi\left(\xi_{i}, \eta_{i}\right) \in \Delta D_{i}$ ，则总体积近似为
$\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}$
(3) 取极限

记 $di}\lambda=\max \limits_{1 \leq 1 \leq n}\left\{d_{i}\right\}$ ，( $d_{i}$ 是小区域 $ΔDi\Delta D_{i}$ 的直径 ) 则体积 $V$ 由如下极限给出
$V=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}$
从以上例子抽象出来就得到二重积分的概念，这类问题要计算在一个平面区域上分布率不均匀的量的总量。

二、二重积分定义

01 二重积分的定义

设 $D$ 是 $x y$ 平面的有界闭区域，函数 $f (x, y)$ 在 $D$ 定义， $I$ 为实数，

若将 $D$ 任意划分成个小区域 $,ΔDn\Delta D_{1}, \Delta D_{2}, \cdots, \Delta D_{n}$ ，

任取 $,n)\left(\xi_{i}, \eta_{i}\right) \in \Delta D_{i},(i=1,2, \cdots, n)$ ，作和
$\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i} \quad\left(\Delta \sigma_{i}\right. 表示 \Delta D_{i} 的面积 )$
总有
$\lim \limits_{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}=I$
( 其中 $di}\lambda=\max \limits_{1 \leq i \leq n}\left\{d_{i}\right\}$ ， $d_{i}$ 是小区域 $ΔDi\Delta D_{i}$ 的直径 )

则称函数 $f (x, y)$ 在 $D$ 上可积， $I$ 称为 $f (x, y)$ 在 $D$ 的二重积分，记为 $∬Df(x,y)dσ\iint \limits_{D} f(x, y) d \sigma$ .

其中， $∬−\iint-$ 积分号， $D -$ 积分区域， $f (x, y) -$ 被积函数， $\sigma-$ 面积元素。

02 二重积分的几何意义

以区域 $D$ 为底，以曲面 $S : z = f (x, y)$ 为顶的曲顶柱体的体积。

03 可积的充分条件

若函数 $f (x, y)$ 在有界区域 $D$ 上分片连续有界，则 $f (x, y)$ 在 $D$ 可积。

三、二重积分的性质

设以下性质中出现的积分均存在

性质1 (线性) ：若 $α,β\alpha, \beta$ 是常数，
$\iint \limits_{D}(\alpha f(x, y)+\beta g(x, y)) d \sigma=\alpha \iint \limits_{D} f(x, y) d \sigma+\beta \iint \limits_{D} g(x, y) d \sigma$
性质2 (可加性) ：若积分区域 $D$ 分成 $D_{1}, D_{2}$ 两个子区域，
$\iint \limits_{D} f(x, y) d \sigma=\iint \limits_{D_{1}} f(x, y) d \sigma+\iint \limits_{D_{2}} f(x, y) d \sigma$
性质3：
$\iint \limits_{D} 1 d \sigma=A_{D} \quad(D\ 的面积)$