Problem Description
In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers:
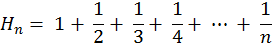
In this problem, you are given n, you have to find Hn.
Input
Input starts with an integer T (≤ 10000), denoting the number of test cases.
Each case starts with a line containing an integer n (1 ≤ n ≤ 108).
Output
For each case, print the case number and the nth harmonic number. Errors less than 10-8 will be ignored.
Sample Input
12
1
2
3
4
5
6
7
8
9
90000000
99999999
100000000Sample Output
Case 1: 1
Case 2: 1.5
Case 3: 1.8333333333
Case 4: 2.0833333333
Case 5: 2.2833333333
Case 6: 2.450
Case 7: 2.5928571429
Case 8: 2.7178571429
Case 9: 2.8289682540
Case 10: 18.8925358988
Case 11: 18.9978964039
Case 12: 18.9978964139
题意:给出 t 组数,每组输入一个数 n,求这个数的调和级数 H(n)
思路:
当 n 很小时,直接打表求即可
当 n 很大时,需要使用欧拉给出的近似公式:,其中 C 是欧拉常数,约等于 0.5772
Source Program
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define PI acos(-1.0)
#define E 1e-9
#define INF 0x3f3f3f3f
#define LL long long
const int MOD=10007;
const int N=10000+5;
const int dx[]= {-1,1,0,0};
const int dy[]= {0,0,-1,1};
using namespace std;
double a[N];
int main(){
a[1]=1;
for(int i=2;i<=10000;i++)
a[i]=a[i-1]+1.0/i;
int t;
scanf("%d",&t);
int Case=1;
while(t--){
int n;
scanf("%d",&n);
if(n<=10000){
printf("Case %d: %.10lf\n",Case++,a[n]);
}
else{
double res=log(n)+1.0/(2*n)+0.57721566490153286060651209;
printf("Case %d: %.10lf\n",Case++,res);
}
}
return 0;
}
 调和级数 H(n) 的计算问题
调和级数 H(n) 的计算问题










 博客围绕调和级数 H(n) 的计算展开,给出 t 组数,每组输入一个数 n 求 H(n)。对于较小的 n 可直接打表求解,对于较大的 n 则需使用欧拉给出的近似公式,还给出了示例输入输出。
博客围绕调和级数 H(n) 的计算展开,给出 t 组数,每组输入一个数 n 求 H(n)。对于较小的 n 可直接打表求解,对于较大的 n 则需使用欧拉给出的近似公式,还给出了示例输入输出。
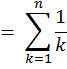
















 408
408

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








