4.1 频率响应概述

 

第4章 放大电路的频率响应

本章讨论的问题

放大电路的频率响应是理解和设计有效电子设备的关键组成部分。本章将探讨以下几个核心问题：

• 为什么要研究放大电路的频率响应?
• 如何测定一个RC网络的频率响应? 怎样画出频率特性曲线?
• 晶体管与场效应管的h参数等效模型在高频信号下还适用吗? 为什么? 如何构造高频等效模型?
• 什么是放大电路的通频带? 哪些因素影响通频带? 如何确定放大电路的通频带?
• 如果放大电路的频率响应不满足要求，应该怎么办?
• 对于放大电路，是通频带愈宽愈好吗? 为什么?
• 为什么集成运放的通频带很窄?

4.1 频率响应概述

4.1.1 研究放大电路频率响应的必要性

频率响应分析对于设计和使用放大电路至关重要。这不仅影响放大倍数的数值，还影响信号的相位，即放大倍数随信号频率变化的特性。

• 通频带的重要性：每个放大电路都有一个特定的通频带，即它能有效工作的频率范围。设计电路时，了解信号的频率范围是必需的，以确保设计的电路能适应这些频率。

• 低频和高频的影响：传统的放大电路模型在低频情况下可能有效，但在高频信号下，晶体管的内部电容效应变得显著，这会影响电路的性能。因此，高频信号的处理需要考虑这些电容，使用高频等效模型。

• 上限频率和下限频率：放大电路的性能不仅受到信号频率的上限的限制，也受到下限频率的影响。这些频率定义了电路能够有效处理信号的频率边界。

测定频率响应和画出特性曲线

• 测定方法：通常使用网络分析仪或频谱分析仪测量电路的频率响应。这些设备能提供输入信号，并测量输出信号的幅度和相位，从而绘制频率响应曲线。

• 绘图：频率特性曲线通常在对数纸上绘制，横坐标为对数频率，纵坐标为增益的对数（分贝dB）。这种表示方法可以清楚地显示通频带及增益随频率的变化。

高频等效模型

为了在高频下准确分析放大电路，需要引入晶体管的高频等效模型，包括它们的内部结电容。这些高频模型有助于更好地理解电路在高频下的行为，并优化设计以满足性能要求。

总结

本章的探讨将使读者能够更深入地理解放大电路在不同频率下的表现，对设计和改进放大电路提供理论支持和实际指导。通过这些分析，设计师能够制定出符合具体应用需求的电路解决方案。

 

4.1.2 频率响应的基本概念

在放大电路设计中，频率响应是一个关键的性能指标，它描述了电路对不同频率信号的处理能力。这部分将详细介绍高通和低通电路的频率响应特性，并阐述其对放大电路性能的影响。

高通电路

高通电路允许高频信号通过，而阻止低频信号。这通常通过耦合电容实现，该电容在高频时呈现较低的阻抗，从而允许信号通过。

高通电路的特性

• 截止频率 𝑓𝑐fc​：是电路开始显著衰减输入信号幅度的频率。在 𝑓𝑐fc​ 时，输出信号的幅度为输入的 122​1​ (约 0.707 倍)，相位滞后45°。
• 频率响应方程：

  

  此方程显示了增益 𝐴(𝑓)A(f) 与频率的依赖关系，指示当频率远高于 𝑓𝑐fc​ 时，输出幅度 ∣𝐴(𝑓)∣∣A(f)∣ 接近1，相位接近 0°。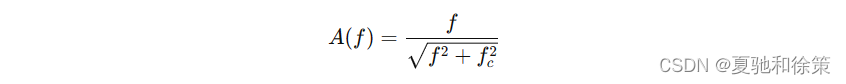

图4.1.1(a)展示了高通电路的配置，图4.1.1(b)为其频率特性曲线，包括幅频特性和相频特性曲线。

低通电路

低通电路允许低频信号通过，而高频信号受到阻挡。这是通过耦合电容以及半导体管极间电容实现的，这些电容在高频时提供较低的阻抗，导致信号损失。

低通电路的特性

• 截止频率 𝑓𝑛fn​：是电路开始显著衰减输入信号幅度的频率。在 𝑓𝑛fn​ 时，输出信号的幅度为输入的 122​1​，相位超前45°。
• 频率响应方程：

  

  此方程显示了增益 𝐴(𝑓)A(f) 与频率的依赖关系，指示当频率远低于 𝑓𝑛fn​ 时，输出幅度 ∣𝐴(𝑓)∣∣A(f)∣ 接近1，相位接近 0°。

图4.1.2(a)展示了低通电路的配置，图4.1.2(b)为其频率特性曲线，包括幅频特性和相频特性曲线。

通频带的定义

放大电路的通频带是指电路能有效处理信号的频率范围，从最低有效频率 𝑓𝑙fl​ 到最高有效频率 𝑓𝑢fu​。通频带的宽度由以下公式确定：

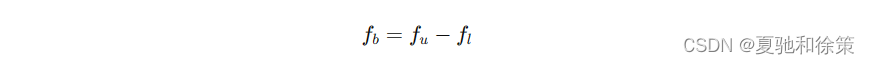
通频带的宽度对于放大电路的应用非常重要，因为它决定了电路能处理的信号类型和速率。

通过理解和应用这些频率响应的基本概念，可以设计出更加精确和高效的放大电路，以满足特定的应用需求。

 

4.1.3 波特图

波特图是在电子工程中广泛使用的一种图形工具，用于展示放大电路如何随频率变化响应不同的信号。该工具尤其对于显示放大电路在宽广频率范围内的性能至关重要。下面我们将详细讨论波特图的构成和分析方法。

波特图的构成

波特图包括两部分：对数幅频特性和对数相频特性。

• 对数幅频特性：幅度以对数刻度（分贝dB）表示，这使得非常大的增益范围可以在同一坐标系内清楚地展示。这种表示方法将乘法运算转换为加法，便于计算和理解。
• 对数相频特性：相位以度（°）表示，通常也用对数刻度来表示频率。

高通电路的波特图

对于高通电路，当频率大于某个截止频率 𝑓𝑐fc​ 时，信号几乎不受衰减；当频率低于 𝑓𝑐fc​ 时，信号衰减显著。在截止频率处，增益下降到最大增益的 122​1​ (约 -3 dB)，相位为 +45°。

公式表示：

• 当 𝑓>>𝑓𝑐f>>fc​ 时，20log⁡∣𝐴(𝑓)∣≈0 dB20log∣A(f)∣≈0 dB，𝜙≈0°ϕ≈0°
• 当 𝑓=𝑓𝑐f=fc​ 时，20log⁡∣𝐴(𝑓)∣=−3 dB20log∣A(f)∣=−3 dB，𝜙=+45°ϕ=+45°
• 当 𝑓<𝑓𝑐f<fc​ 时，增益以每十倍频率下降 20 dB 的速率下降。

低通电路的波特图

对于低通电路，当频率小于某个截止频率 𝑓𝑛fn​ 时，信号几乎不受衰减；当频率大于 𝑓𝑛fn​ 时，信号衰减显著。在截止频率处，增益下降到最大增益的 122​1​ (约 -3 dB)，相位为 -45°。

公式表示：

• 当 𝑓<<𝑓𝑛f<<fn​ 时，20log⁡∣𝐴(𝑓)∣≈0 dB20log∣A(f)∣≈0 dB，𝜙≈0°ϕ≈0°
• 当 𝑓=𝑓𝑛f=fn​ 时，20log⁡∣𝐴(𝑓)∣=−3 dB20log∣A(f)∣=−3 dB，𝜙=−45°ϕ=−45°
• 当 𝑓>𝑓𝑛f>fn​ 时，增益以每十倍频率上升 20 dB 的速率下降。

近似的波特图

在实际应用中，为简化分析，波特图通常被近似为由几段直线组成。这种近似假设在关键频率点（如 10𝑓𝑐10fc​ 和 0.1𝑓𝑐0.1fc​）的附近相位和幅度变化是线性的。

结论

通过波特图，设计师可以直观地看到放大电路在整个操作频率范围内的性能。这种图形表示法不仅帮助工程师优化电路设计，还有助于识别可能的性能问题，如增益过低或不希望的相位变化。通过这种方法，可以确保放大电路在预定的应用中达到最佳性能。