2.1 随机变量

---

• 博主介绍：夏驰和徐策

• 所属专栏：

• 上期回顾：

---

2.1.1 随机变量的概念

学习步骤：

如果我要学习随机变量的概念和随机变量的分布函数，我会按照以下步骤进行：

1. 学习基本概念首先，我会了解随机变量的基本概念，包括样本空间、事件、概率等概念。然后，我会学习随机变量的定义，即将样本空间中每一个可能的事件都映射到实数轴上。我还会学习随机变量的取值范围、分布函数、概率密度函数等相关概念。

2. 学习分布函数其次，我会深入学习随机变量的分布函数。我会了解分布函数的定义和性质，包括累积分布函数和概率密度函数。我会学习不同类型的分布函数，例如均匀分布、正态分布、伽玛分布等，并掌握它们的特征和应用。

3. 探究统计推断最后，我会学习如何使用随机变量和分布函数进行统计推断。我会学习如何估计分布函数的参数、如何进行假设检验以及如何进行置信区间估计等。我也会探究如何使用随机变量来建立概率模型，例如使用概率分布来描述一组随机数据。

总的来说，学习随机变量和分布函数需要掌握一些数学知识，包括概率论、统计学和微积分等。我会通过阅读教材、参加课程和练习习题等方式来逐步掌握这些知识和技能。同时，我也会尽可能地多做实践，例如使用计算机模拟随机变量的分布以及分析实际数据的分布等，以便更好地理解和应用这些概念。

2.1.1 我的理解

随机变量是概率论和统计学中一个重要的概念，它是将样本空间中每一个可能的事件都映射到实数轴上的函数。随机变量通常用大写字母来表示，例如 X、Y、Z 等。随机变量的取值通常用小写字母来表示，例如 x、y、z 等。

在更具体地定义随机变量之前，我们先来了解一下样本空间和事件的概念。在概率论中，样本空间是指一个试验中所有可能的结果组成的集合，通常用 S 表示。例如，掷一枚硬币的样本空间可以表示为 S = {正面，反面}。事件是指样本空间的一个子集，通常用 A、B、C 等字母来表示。例如，掷一枚硬币出现正面的事件可以表示为 A = {正面}。

随机变量的定义可以通过以下两种方式之一来给出：

1. 离散型随机变量：如果随机变量 X 取有限或可数个取值，我们称 X 为离散型随机变量。在这种情况下，X 的取值通常是整数或者是一些离散的有限或无限序列。例如，掷一枚骰子得到的点数就是一个离散型随机变量，它的取值为 {1, 2, 3, 4, 5, 6}。

2. 连续型随机变量：如果随机变量 X 取所有实数值或某个实数区间内的值，我们称 X 为连续型随机变量。在这种情况下，X 的取值通常是一个区间。例如，一个人的身高就是一个连续型随机变量，它可以取到任意实数值。

无论是离散型随机变量还是连续型随机变量，随机变量都可以用分布函数来描述。分布函数是指随机变量取某一值以下的概率，它是一个非降、右连续的函数，通常用 F(x) 表示。对于离散型随机变量，分布函数可以写成一个累积求和的形式，而对于连续型随机变量，分布函数可以写成一个积分的形式。

2.1.2 随机变量的分布函数我的理解

随机变量的分布函数（也称累积分布函数）是指随机变量取某一值以下的概率，它是一个非降、右连续的函数，通常用 F(x) 表示。

对于离散型随机变量，分布函数可以表示为：

F(x) = P(X ≤ x) = ∑ P(X = xi)，其中 xi 是随机变量 X 取值的集合。

也就是说，分布函数 F(x) 在 x 点的取值，等于随机变量 X 小于或等于 x 的所有取值的概率之和。

对于连续型随机变量，分布函数可以表示为：

F(x) = P(X ≤ x) = ∫ f(t) dt，其中 f(t) 是随机变量 X 的概率密度函数。

也就是说，分布函数 F(x) 在 x 点的取值，等于随机变量 X 小于或等于 x 的概率，即 X 的概率密度函数在区间 [0, x] 上的积分。

随机变量的分布函数具有以下性质：

1. F(x) 是一个非降函数，即对于任意的 x1 < x2，有 F(x1) ≤ F(x2)。

2. F(x) 是一个右连续函数，即对于任意的 x0，有 lim F(x) = F(x0+)。

3. 当 x → -∞ 时，F(x) → 0；当 x → +∞ 时，F(x) → 1。

通过分布函数，我们可以方便地计算随机变量在某个区间内取值的概率，也可以更好地理解随机变量的性质和规律。

总结：

随机变量是一种数学对象，它描述的是随机事件的结果，可以是离散的或连续的。随机变量的概念包含以下重点和难点：

1. 随机变量的定义：随机变量是一个变量，它的取值是由一个随机过程所决定的，通常用大写字母 X 表示。

2. 随机变量的分类：随机变量可以是离散型的或连续型的。离散型随机变量的取值有限或可数，而连续型随机变量的取值是一个连续的区间。

3. 随机变量的概率分布：随机变量的概率分布可以是概率质量函数（离散型随机变量）或概率密度函数（连续型随机变量）。概率分布描述了随机变量取各个取值的概率大小。

4. 随机变量的期望和方差：随机变量的期望是随机变量取值的加权平均值，方差则是随机变量的取值与期望的偏离程度的平均值。

随机变量的分布函数是一个非降、右连续的函数，用来描述随机变量小于或等于某一值的概率。它的重点和易错点包括：

5. 分布函数的定义和性质：分布函数是随机变量取某一值以下的概率，是一个非降、右连续的函数。其性质包括：非降、右连续、在负无穷处趋近于0、在正无穷处趋近于1。

6. 离散型随机变量的分布函数：离散型随机变量的分布函数可以表示为概率质量函数的累积和。

7. 连续型随机变量的分布函数：连续型随机变量的分布函数可以表示为概率密度函数的积分。

8. 计算概率的方法：通过分布函数可以计算随机变量在某个区间内取值的概率，需要注意计算上下限、区间包含/不包含等细节。

9. 概率质量函数和概率密度函数的转换：概率密度函数和概率质量函数可以通过积分和求和相互转换，但需要注意两者的定义域和取值范围不同。

总的来说，理解随机变量和分布函数的概念和性质，掌握计算概率的方法，注意离散型和连续型随机变量的差异和转换方法

随机试验的结果有些本身就是数量,例如,一只灯泡的寿命,每天的最高气温等随机试验的结果有些不是数量,例如,检查一个产品,结果可能是“合格”与“不合格”但是我们可以将其数量化,如用“1”表示“合格”，用“0”表示“不合格”.这样,随机试验的结果就是随机变化的变量.把随机试验的结果数量化,便于应用数学知识研究随机现象，使对随机现象的研究更深人和简单.先看两个例子

【例2.1】 有朋自远方来,他可能乘船、乘火车,或者乘飞机，记1={乘船},{乘火车),={乘飞机)，这就是以Ω=(}为样本空间的随机试验，现考虑该客人的旅费，很定乘船、火车与乘飞机的单价分别为 100 元,200 元,300元,则所需旅费就是如下实值单值函数。

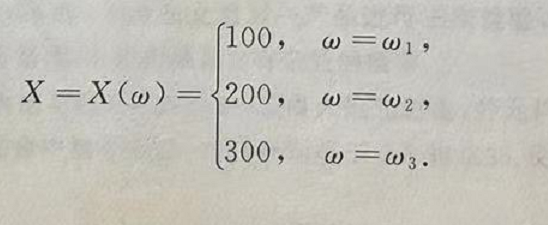
易见,X=X()是随试验结果而变化的交量，称之为随机变量.它的定义城是样本空间Ω,值域为{100,200,300}.

【例2.22】将一枚硬币连续拋 3次,观察是正面朝上的情况,如果用1表示正面朝上。表示反面朝上,那么试验的样本空间为2=1(1,1,1),(1,1,0)，(1,0,1)，(1.0,0）， (0,1,1)，(0,1,0），(0,0,1) (0.0,0)〉若用 X 表示正面朝上的次数,那么叉 是一个变量,它的取值随试验结果而变化，是定义在样本空间上的西数，具体写出来就是10,0=(0,0,0).孓=X(a)=（0,0,1 或(0,1,0）或(1,0,0），12∞=（1,1,0）或(1,0,1） 或(0,1,1)，=¢1,1,1)以上函数我们称为随机变量,它的定义域是样本空间2，值域为{0,1,2,3)

下面给出随机变量的定义

定义2.1 设随机试验的样本空间为Ω={},X=X()是定义在样本空间Ω上的实值单值函数,称X=X()为随机变量.常用大写字母 X,Y,Z等表示随机量,其取值常用小写字母x,y,z等表示.

定义2.1表明：随机变量又是样本点的一个实值单值函数.一个样本点只能对应一个实数,不同样本点可以对应不同的实数,也可以对应同一个实数随机变量的取值随试验的结果而定,在试验之前不能预知它取到的值,且它的取值有一定的概率,这说明了随机变量与普通两数和普通变量有着本质的区别.引人随机变量后,我们很容易用随机变量表示随机事件和随机事件发生的概率。例如，用随机变量 区 表示掷一枚骰子朝上一面的点数，则{X一1}和{X＜3}分别表示事件“朝上一面的点数为 1”和“朝上一面的点数不超过 3”两事件，而P{X=1),P{X＜=3}则分别表示两事件发生的概率.

2.1.2 随机变量的分布函数

下面引人随机变量的分布函数的概念．——什么是分布函数

定义2.2 设X是一个随机变量,对任意实数x,称事件{X＜=x}发生的概率.

F(x)=P{X<=x}(-∞<x<∞) (2.1)

为随机变量 了的分布函数，且称叉服从F(x),记为x~F(x).

由分布函数的定义易知，对任意实数a,6(a二6），有Pia<x≤61=Px≤6-P1x≤0=F66-FCa），PX≥a=1-Px≤a=1-Fca可见,若已知区的分布函数F(z），那么，计算叉落在某个区间的概率就非常方便了.由于分布两数是一个普通的两数,通过它我们可以方便地利用数学方法来研究

总结：

{x|x(w)=a}:事件A

{x=a}：事件A

p{x=a}:事件A发生的概率

随机变最.O5容易证明分布两数下(天)具有以下三条基本性质

①单调性：P(w)是定义在路不实数轴（一a014∞0>上的单调非减西数，即对任

意的21＜z2，有FCZD<FCZ2);

(2）有界性：对任意的2，有0<F)≤1,且

F(-∞=limF=0,

F(+∞= limF(=1.

(3）右连续性：F（z)是， 的右连续西数，即对任意的工。，有lim FKZD=FCEO.

还可以证明，满足这三个基本性质的西数一定是某个随机变量的分布西数-从而

这三个基本性质成为判别某个的数是否能成为分布西数的充要条什：

【例2.3】证明FC)=一larctanz te元三：一8三2二十∞是一个分和晒数。

证显然厂(z）在整个数轴上是连续、 严格单调递增两数，且F（+∞)一1

F(一∞)一0,因此它满足分布两数的三条基本性质,故F(z)是一个分布函数

该函数称为柯西分布西数

【例 2.4】 向半径为，的圆内随机拋一点,求此点到网心的距离叉 的分布函数，

并求『了＞

解 事件《X≤z}表示所抛一点落在半径为，的圆内

若z＜0，（X＜z}为不可能事件,则FOD-Px<z=0:

若z≥r，(x＜二)为必然事件,则F(D-Px<z=1

“若0＜z＜r,由几何概型知

F(X) = PIX < 2) _ 12?

Ter?

从而了的分布两数为I <0,E(x) =0 <r<rA

P18=③1=1=28≤=1-F)-1-135

总结：

在引人了随机变量和分布两数后，我们就可以利用高等数学的许多结果和方法

来研究各种随机现象了.下面将分别按照离散型和连续型两种类别来更深人地研究

随机变量及其分布两数，其他类型的随机变量本书不作研究．

---

2023/4/13

宋浩网课观看心得笔记：

随机变量的概念：