[SCOI2013]数数（数位dp）

最新推荐文章于 2025-02-17 20:45:43 发布

原创最新推荐文章于 2025-02-17 20:45:43 发布 · 220 阅读

1 ·

CC 4.0 BY-SA版权

数位dp 专栏收录该内容

4 篇文章

订阅专栏

这篇博客介绍了一道关于数位DP的题目，作者通过分析如何优化状态转移，将复杂度从O(NB)降低到O(1)，并提供了详细的解题思路和简化后的代码实现，讨论了数位计数、前缀和以及优化技巧。

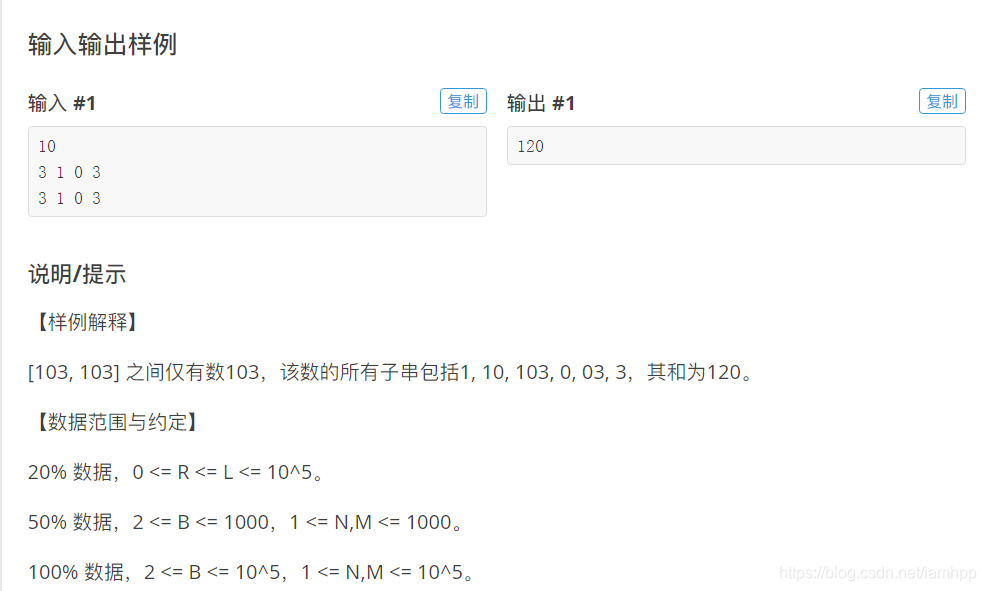
题意

在这里插入图片描述

分析

这道破题怎么写了我这么久啊啊！！菜死了TAT
很明显要数位 $d p$ 。
设 $num_{pos,limit,zero}$ 表示从高到低考虑到第 $p o s$ 位，有没有顶着上界，是否有前导零的数的个数， $s1_{pos,limit,zero}$ 表示从高到低考虑到第 $p o s$ 位，有没有顶着上界，是否有前导零的前缀串之和，比如 $12345$ 的前缀串是 $1, 12, 123, 1234, 12345$ 。那么转移的话枚举当前最高位的数 $i$ ，考虑 $i$ 对单独一个 $p o s$ 位数的贡献，令 $Ti=∑j=0iBjT_{i}=\sum\limits_{j=0}^{i}B^j$ ，那贡献是 $i*T_{pos}$ 。总共有 $n u m$ 个数，因此 $s1pos,limit,zero=∑i=0ups1pos−1,limit&&i==up,zero&&i==0+i∗Tpos∗nums1_{pos,limit,zero}=\sum\limits_{i=0}^{up}s1_{pos-1,limit\&\&i==up,zero\&\&i==0}+i*T_{pos}*num$ 。设 $s2_{pos,limit,zero}$ 表示从高到低考虑到第 $p o s$ 位，有没有顶着上界，是否有前导零的所有子串之和。那么转移是类似的，就是 $p o s - 1$ 位的子串和加上最高位参与的前缀串之和即可。需要注意的是，如果有前导 $0$ ，那最高位选 $0$ 前缀串之和是不能算进 $s 2$ 的。
这样子的复杂度是 $O (N B)$ 的。
然后发现转移的时候，只用分三种情况， $i = 0$ ， $i = u p$ ， $i∈[1,up−1]i\in[1,up-1]$ 。第三种的每个 $i$ 是等价的，可以通过等差数列求和来快速得到。转移复杂度这样子就降到了 $O (1)$ 。
总之是一道不是很难的题（~~为什么我感觉这么难啊~~

代码如下（注释掉的部分是暴力转移的）

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

void debug_out(){
    cerr << endl;
}
template<typename Head, typename... Tail>
void debug_out(Head H, Tail... T){
    cerr << " " << to_string(H);
    debug_out(T...);
}
#ifdef local
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
#else
#define debug(...) 55
#endif

const int N = 1e5 + 5, maxn = 1e5, mod = 20130427;
int T[N], a[N], B, ans;
struct DP{
	int n, s1, s2;
}dp[N][2][2];
int vis[N][2][2];
DP dfs(int pos, int f1, int f2){
	if(pos == -1) return {1, 0, 0};
	if(vis[pos][f1][f2]) return dp[pos][f1][f2];
	vis[pos][f1][f2] = 1;
	int up = f1? a[pos]: B - 1;
	DP res = {0, 0, 0};
	/*for(int i = 0; i <= up; i++){
		DP t = dfs(pos - 1, f1 && i == up, f2 && i == 0);
		res.n = (res.n + t.n) % mod;
		res.s1 = (res.s1 + (LL)t.n * i % mod * T[pos] % mod + t.s1) % mod;
		res.s2 = (res.s2 + t.s2 + (LL)t.n * i % mod * T[pos] % mod + t.s1 * (!(f2 && i == 0))) % mod;
	}*/
	int i = 0;
	DP t = dfs(pos - 1, f1 && i == up, f2 && i == 0);
	res.n = (res.n + t.n) % mod;
	res.s1 = (res.s1 + (LL)t.n * i % mod * T[pos] % mod + t.s1) % mod;
	res.s2 = (res.s2 + t.s2 + (LL)t.n * i % mod * T[pos] % mod + t.s1 * (!(f2 && i == 0))) % mod;
	if(up > 0){
		i = up;
		t = dfs(pos - 1, f1 && i == up, f2 && i == 0);
		res.n = (res.n + t.n) % mod;
		res.s1 = (res.s1 + (LL)t.n * i % mod * T[pos] % mod + t.s1) % mod;
		res.s2 = (res.s2 + t.s2 + (LL)t.n * i % mod * T[pos] % mod + t.s1 * (!(f2 && i == 0))) % mod;
		if(up > 1){
			int s = ((LL)up * (up - 1) / 2) % mod;
			t = dfs(pos - 1, 0, 0);
			res.n = (res.n + (LL)t.n * (up - 1) % mod) % mod;
			res.s1 = (res.s1 + (LL)t.n * s % mod * T[pos] % mod + (LL)t.s1 * (up - 1) % mod) % mod;
			res.s2 = (res.s2 + (LL)t.s2 * (up - 1) + (LL)t.n * s % mod * T[pos] % mod + (LL)t.s1 * (up - 1) % mod) % mod;
		}
	} 
	return dp[pos][f1][f2] = res;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> B;
	T[0] = 1;
	for(int i = 1; i <= maxn; i++) T[i] = ((LL)T[i - 1] * B % mod + 1) % mod;
	int n;
	cin >> n;
	n--;
	for(int i = n; i >= 0; i--) cin >> a[i];
	if(a[n]){
		for(int i = 0; i <= n; i++){
			if(a[i]){
				a[i]--;
				break;
			}
			a[i] = B - 1;
		}
		if(!a[n]) n--;
		ans -= dfs(n, 1, 1).s2;
	}
	cin >> n;
	n--;
	for(int i = n; i >= 0; i--) cin >> a[i];
	memset(vis, 0, sizeof(vis));
//	debug(ans);
	ans += dfs(n, 1, 1).s2;
	cout << (ans % mod + mod) % mod << '\n';
	return 0;
}