
一、理论
1. 概述
这是一个关于视觉SLAM(Simultaneous Localization and Mapping)建图的全面概述。我们将从基本概念讲起,逐步深入到核心流程、关键技术、不同流派、挑战与未来趋势。
视觉SLAM建图概述
1. 什么是SLAM?
想象一下你被蒙着眼睛带到一个完全陌生的房间,然后摘下眼罩。你需要做什么?
- 定位(Localization)
:你需要通过观察周围的环境(墙壁、家具)来确定自己在哪。
- 建图(Mapping)
:同时,你需要在脑中构建出这个房间的地图(家具的位置、房间的形状)。
SLAM(即时定位与地图构建)解决的就是这个问题。它指的是一个移动设备(如机器人、无人机、手机)在未知环境中,仅依靠自身传感器,一边估算自己的运动轨迹(定位),一边构建周围环境的地图(建图)。
这是一个“鸡生蛋,蛋生鸡”的问题:
准确的定位需要一张精确的地图。
构建精确的地图需要准确的定位信息。
SLAM技术就是为了同时解决这两个相互依赖的问题。
2. 什么是视觉SLAM (Visual SLAM, VSLAM)?
当SLAM系统主要使用的传感器是相机时,我们就称之为视觉SLAM。相机作为信息来源,成本低廉、信息丰富(可以获取颜色、纹理、形状等),使其成为SLAM领域最热门的研究方向之一。
根据使用的相机类型,VSLAM可以分为:
- 单目SLAM (Monocular SLAM)
:只使用一个相机。优点是成本极低、部署简单。缺点是存在尺度不确定性(无法仅凭单张图片判断物体的真实大小和距离),且对快速运动和纯旋转比较敏感。
- 双目SLAM (Stereo SLAM)
:使用两个固定在一起的相机,像人的双眼。优点是可以利用视差原理直接计算深度,解决了单目SLAM的尺度不确定性问题。缺点是计算量稍大,且有效测距范围受限于双目基线(两个相机间的距离)。
- RGB-D SLAM
:使用一个能同时提供彩色图像(RGB)和深度信息(Depth)的相机,如Kinect、RealSense。优点是直接拥有了深度信息,建图和定位难度大大降低。缺点是深度相机通常在室外、远距离或透明物体上表现不佳。
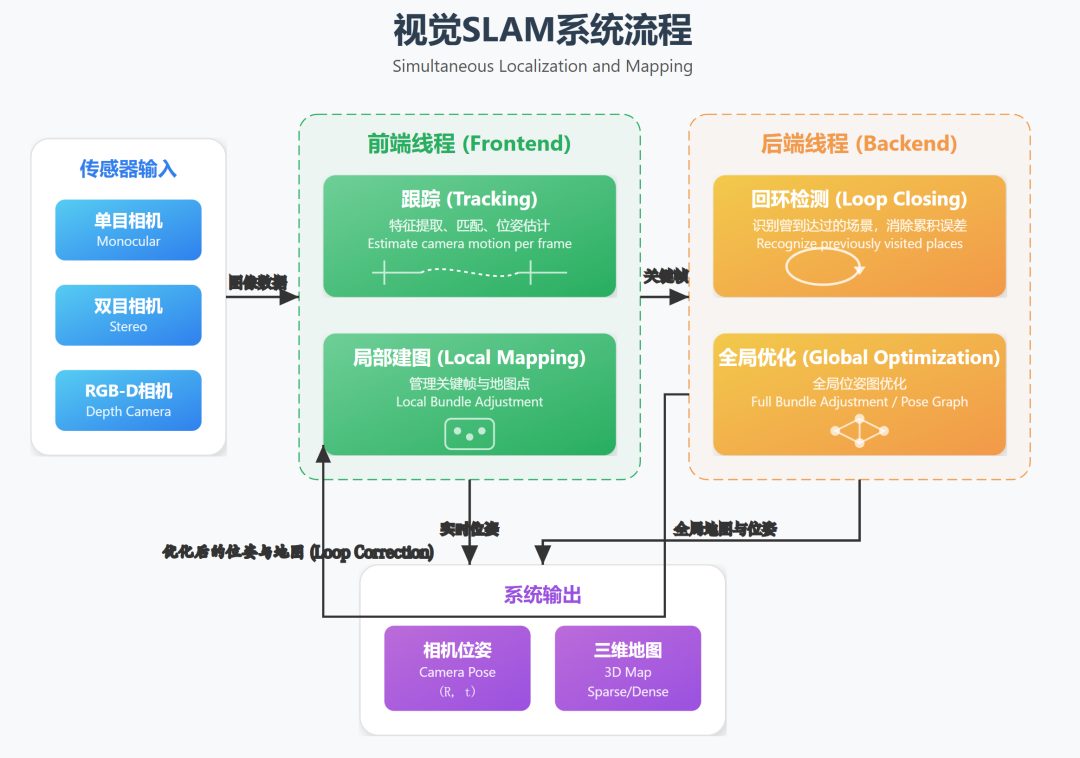
3. 视觉SLAM的核心工作流程
一个完整的VSLAM系统通常可以分为以下几个模块,像一条流水线一样协同工作:
(1) 传感器数据输入 (Sensor Input)
获取相机拍摄的连续图像帧。对于更鲁棒的系统,还会融合IMU(惯性测量单元)的数据,形成VIO(视觉惯性里程计),以应对快速运动或图像纹理缺失的情况。
(2) 前端 / 视觉里程计 (Frontend / Visual Odometry, VO)
前端的主要任务是估算相邻图像帧之间的相机运动,并提供一个局部的地图。它像一个短跑运动员,关注于“下一步该怎么走”。
- 特征提取与匹配 (Feature Extraction & Matching)
:在图像中寻找稳定、可区分的点(如角点、斑点),称为“特征点”(如ORB, SIFT, SURF)。然后在连续的帧之间进行匹配,找到同一个空间点在不同图像中的投影。
- 运动估计 (Motion Estimation)
:根据匹配的特征点,利用对极几何、PnP算法等数学方法,计算出相机从上一帧到当前帧的位姿变换(旋转和平移)。
- 局部地图构建
:将新的特征点(也称为地图点或路标点)加入到一个临时的、小范围的地图中。
前端会不可避免地产生累积误差,就像走路时每一步都有微小偏差,走得越远,总的偏差就越大。
(3) 后端优化 (Backend Optimization)
后端是整个系统的“大脑”,负责处理前端传来的带有累积误差的数据,进行全局优化,得到一个全局一致的轨迹和地图。它像一个马拉松策略师,关注于“整体路线是否正确”。
- 核心方法:图优化 (Graph Optimization)
:这是现代VSLAM的主流方法。
- 节点 (Nodes)
:图中的节点代表了不同时刻的相机位姿和空间中的路标点。
- 边 (Edges)
:边代表了节点之间的观测约束。例如,一个位姿节点和路标点节点之间的边,表示“在这个位姿下观测到了这个路标点”。
- 优化目标
:调整所有节点的位置(相机位姿和路标点坐标),使得所有观测约束的总误差(例如,重投影误差)最小。这个过程通常通过非线性最小二乘法(如高斯-牛顿法、列文伯格-马夸尔特法)来求解。BA (Bundle Adjustment) 是图优化的“黄金标准”。
- 节点 (Nodes)
(4) 回环检测 (Loop Closing)
回环检测是后端优化中至关重要的一环,是解决累积误差的“大招”。
- 目的
:当相机回到一个曾经到过的地方时,系统需要能够识别出来。
- 方法
:通常使用词袋模型 (Bag-of-Words, BoW),如DBoW2。它将图像中的特征点“字典化”,把一幅图像快速转换成一个稀疏的向量。通过比较当前帧与历史所有关键帧的向量相似度,可以高效地判断是否回到了旧地。
- 作用
:一旦检测到回环,就在后端的优化图中添加一个强大的约束(当前位置和历史位置是同一个地方)。然后后端会重新进行全局优化,将累积的误差“拉”回去,使得整个地图和轨迹变得高度一致。
(5) 建图 (Mapping)
根据优化后的相机位姿和路标点,最终构建出环境的地图。地图的形式可以是:
- 稀疏地图 (Sparse Map)
:只包含路标点和相机轨迹。主要用于定位,无法用于导航或可视化。
- 稠密/半稠密地图 (Dense/Semi-Dense Map)
:通过像素级的深度估计,构建出密集的点云或网格模型,可以清晰地展现环境的3D结构,用于导航、避障和AR等应用。
4. VSLAM的主要技术流派
根据前端处理图像方式的不同,主要分为两派:
(1) 特征点法 (Feature-based Method)
- 原理
:依赖于上文提到的特征点提取和匹配。
- 优点
:对光照变化和动态物体有较好的鲁棒性,计算效率高,技术成熟。
- 缺点
:如果环境中缺乏稳定特征(如白墙、走廊),系统容易失效。生成的地图是稀疏的。
- 代表算法
:PTAM (开创性工作), ORB-SLAM2/3 (目前最流行和全面的框架之一)。
(2) 直接法 (Direct Method)
- 原理
:不计算特征点,而是直接根据像素的灰度信息,通过最小化光度误差来估计相机运动。
- 优点
:在特征缺失的场景中也能工作,可以构建半稠密甚至稠密的地图。
- 缺点
:对光照变化非常敏感,假设灰度不变,对相机内参和曝光要求较高。
- 代表算法
:LSD-SLAM (半稠密), DSO (稀疏直接法), SVO (半直接法)。
5. 挑战与发展趋势
主要挑战:
- 动态环境
:场景中的行人、车辆会干扰静态地图的假设。
- 鲁棒性
:在光照剧烈变化、快速运动、纹理缺失等极端条件下容易失败。
- 长期运行
:如何在大规模、长时间的运行中保持地图的一致性和效率。
- 计算资源
:稠密建图和实时优化对计算能力要求很高。
- 动态环境
发展趋势:
- 与深度学习结合
:利用深度学习进行更鲁棒的特征提取、深度估计、语义分割(识别物体类别)和回环检测。
- 语义SLAM
:不仅构建几何地图,还构建包含物体信息的语义地图(如“这是一张椅子”,“那是一扇门”),让人机交互和高级任务成为可能。
- 多传感器融合
:将视觉与IMU、GPS、LiDAR、轮式里程计等更紧密地融合,取长补短,提高系统的鲁棒性和精度。
- VIO/VINS
(视觉惯性导航系统) 已成为移动设备上的标配。
- 与深度学习结合
6. 应用领域
- 增强现实 (AR)
/ 虚拟现实 (VR):实现虚拟物体在真实环境中的准确定位和交互。
- 机器人
:为扫地机器人、无人机、自主导航机器人提供定位和导航能力。
- 自动驾驶
:作为高精度地图制作和定位的辅助手段。
- 三维重建
:快速对室内外环境进行三维建模。
总而言之,视觉SLAM是一个融合了计算机视觉、状态估计理论、优化理论和机器人学的交叉领域。它赋予了机器“看懂”世界并知道自己身在何方的能力,是实现真正智能移动设备的核心技术之一。
2. 单目稠密重建
我们来深入探讨视觉SLAM中的一个非常重要且具有挑战性的分支——单目稠密重建 (Monocular Dense Reconstruction)。
这可以看作是视觉SLAM建图的“终极形态”之一,因为它旨在从单个移动的相机中,恢复出场景中几乎每一个像素的3D结构。
1. 什么是单目稠密重建?
- 单目 (Monocular)
:整个过程只使用一个普通的相机作为输入。
- 稠密 (Dense)
:目标是为输入图像中的每一个(或绝大多数)像素计算出其在三维空间中的深度(depth)信息。最终结果通常是一个密集的点云或者一个连续的表面模型(Mesh)。
- 重建 (Reconstruction)
:最终目标是构建出环境的3D几何模型。
直观理解:想象你只用一只眼睛(单目)观察世界,然后边走边看(移动相机)。你的大脑能够根据物体在你视野中移动的方式(运动视差),推断出它们的远近关系和形状,最终在你脑中形成一个立体的场景模型。单目稠密重建就是让计算机来完成这个过程。
2. 核心挑战:尺度不确定性 (Scale Ambiguity)
这是单目视觉的根本难题。
仅凭单张图片,你无法判断一个物体是“近处的小物体”还是“远处的大物体”。例如,你看到的桌上的一个小模型汽车和远处的一辆真车,在你的视网膜上可能成像大小一样。
如何解决?
单目稠密重建系统通过相机的运动来解决这个问题。当相机移动时,近处的物体在图像上移动得快,远处的物体移动得慢(这就是运动视差)。通过三角化这些运动,系统可以恢复出场景的相对结构。
但是,这只能恢复相对结构。整个重建出来的场景的大小(即绝对尺度)是未知的。如果你把相机的移动轨迹和所有点的3D坐标都放大或缩小两倍,它们投影到图像上的结果是完全一样的。
在实际应用中,通常需要一个先验信息来确定绝对尺度,例如:
知道相机移动的真实距离(如通过IMU或轮式里程计)。
知道场景中某个物体的真实尺寸(如一个A4纸的大小)。
3. 单目稠密重建的技术流程
一个典型的单目稠密重建系统通常包含以下几个关键步骤,这是一个“先定位,后建图”的流程:
第1步:相机位姿估计 (Camera Pose Estimation)
这是整个流程的基石。在重建任何东西之前,我们必须精确地知道相机在每一时刻的位置和姿态(朝向)。这个过程本身就是一个视觉SLAM或**视觉里程计 (VO)**系统。
- 方法
:通常使用一个成熟的、以定位为主要目的的VSLAM系统作为前端,例如 ORB-SLAM2/3 (特征点法) 或 DSO (直接法)。
- 产出
:
- 相机轨迹 (Camera Trajectory)
:一系列精确的相机位姿。
- 稀疏/半稠密地图 (Sparse/Semi-Dense Map)
:由关键帧和一些稳定的3D路标点构成。这个地图本身不是最终目标,但它为后续的稠密重建提供了重要的几何约束。
第2步:稠密深度图估计 (Dense Depth Estimation)
有了精确的相机位姿后,我们就可以为选定的关键帧 (Keyframes) 计算稠密的深度图了。这一步的核心技术是多视角立体视觉 (Multi-View Stereo, MVS)。
原理:
选择一个参考帧 (Reference Frame),我们想为这个帧的每个像素计算深度。
再选择几个视角不同但与参考帧有重叠区域的源帧 (Source Frames)。
对于参考帧中的一个像素
(u, v),我们沿着它的视线方向,假设一系列可能的深度值。对于每一个假设的深度值
d,我们可以计算出其对应的3D点P。将这个3D点
P重新投影到各个源帧中,得到对应的像素点。比较参考帧中像素
(u, v)周围的小图像块(Patch)与源帧中对应投影点周围的图像块。如果它们的光度一致性 (Photometric Consistency) 很高(即长得很像),说明我们假设的深度值d很可能是正确的。通过遍历所有可能的深度并找到光度一致性最好的那个,我们就得到了该像素的深度。这个过程被称为平面扫描 (Plane Sweeping)。
优化:原始的深度图会充满噪声和误匹配。因此需要进行正则化和滤波,例如使用马尔可夫随机场 (MRF) 等方法,使得深度图在空间上更平滑,更符合物理世界的规律。
第3步:深度图融合 (Depth Map Fusion)
我们现在为多个关键帧都生成了各自的稠密深度图。但每个深度图都是从单一视角出发,包含噪声和遮挡。为了得到一个完整、一致的全局模型,我们需要将它们融合起来。
核心数据结构:TSDF (Truncated Signed Distance Function)
这是目前最主流和最高效的融合方法。想象一下,我们将整个三维空间划分成一个个小方块,称为体素 (Voxel)。对于每个体素,我们存储一个值:它到最近的物体表面的有符号距离。在物体内部为负,外部为正,在表面上为零。
"Truncated"(截断)意味着我们只关心表面附近的距离,离表面太远的体素我们就不精确计算了,这能节省大量内存。
融合过程:
遍历每一个关键帧的深度图。
将深度图上的每一个像素点,根据其深度值和相机位姿,反向投影到全局的TSDF体素网格中。
当一个3D点投影到体素网格时,它会更新其路径上所有体素的TSDF值(通过加权平均)。
经过多个深度图的不断更新,噪声点因为不一致性会被平均掉,而真实的表面会因为多次观测而得到加强,最终形成一个平滑、精确的隐式表面表示。
第4步:表面网格生成 (Mesh Extraction)
TSDF体素网格只是一个中间表示。为了得到可用于可视化或3D打印的表面模型,我们需要从TSDF中提取出表面网格(Mesh)。
- 常用算法:Marching Cubes (移动立方体)
该算法遍历所有体素,检查每个体素的八个顶点的TSDF值的正负号。根据正负号的组合(共256种情况),可以确定表面是如何穿过这个体素的,并生成对应的小三角面片。将所有体素生成的小三角面片拼接起来,就得到了最终的3D网格模型。
4. 深度学习的崛起
近年来,深度学习极大地推动了单目稠密重建的发展,主要体现在两个方面:
单帧深度估计 (Single-Image Depth Estimation):
- 有监督学习
:使用带有真实深度(如用LiDAR或Kinect采集)的数据集进行训练。代表作有MiDaS。
- 自监督学习
:仅使用连续的视频帧进行训练。通过预测一个帧的深度和两帧间的位姿,将该帧“扭曲”到下一帧,然后最小化两帧的光度差异。这避免了对昂贵真值数据的依赖。代表作有Monodepth2。
- 原理
:训练一个深度神经网络(如U-Net架构),输入一张RGB图像,直接输出一张深度图。
- 方法
:
- 优点
:速度快,可以从单张静止图像预测深度。
- 缺点
:依然存在尺度不确定性,且泛化能力和精度通常不如传统MVS方法。
神经辐射场 (Neural Radiance Fields, NeRF):
- 原理
:这是革命性的方法。它不再遵循“位姿->深度->融合”的流程。而是训练一个小型神经网络来隐式地表示整个3D场景。
- 输入
:一个3D坐标
(x,y,z)和一个相机视角方向(θ,φ)。 - 输出
:该点在该视角下的颜色 (RGB) 和密度 (σ)。
- 工作方式
:通过从大量已知位姿的图像中采样像素光线,并最小化渲染出的颜色与真实颜色的差异,网络学会了整个场景的3D结构和外观。
- 优点
:能生成照片级真实的渲染效果和高质量的几何细节。
- 缺点
:训练和渲染都非常耗时(尽管最新的研究正在极大改善这一点),并且需要事先知道精确的相机位姿。
总结
单目稠密重建是一个复杂但成果斐然的领域。
- 传统方法
(如基于MVS和TSDF融合)流程清晰,几何精度高,是工业界和学术界经过验证的可靠方案。
- 深度学习方法
,特别是自监督深度估计和NeRF,为该领域注入了新的活力,在某些方面(如单帧预测、渲染质量)展现出巨大潜力,并逐渐成为研究热点。
未来的趋势很可能是将传统几何方法的稳定性和精度与深度学习的强大先验和表示能力相结合,以实现更鲁棒、更高效、更精细的实时单目三维重建。
3. 立体视觉
我们来详细讲解立体视觉 (Stereo Vision)。这是一个在计算机视觉和机器人领域中极其重要的概念。
1. 核心思想:模仿人类双眼
立体视觉的灵感完全来自于人类的双眼视觉系统。
想象一下:你伸出一根手指放在眼前,先闭上左眼用右眼看,再闭上右眼用左眼看。你会发现手指相对于背景的位置发生了移动。这个位置差异就叫做视差 (Parallax / Disparity)。
我们的大脑天生就会利用这个视差信息来判断物体的远近:
- 近处的物体
:视差很大(移动得厉害)。
- 远处的物体
:视差很小(几乎不移动)。
立体视觉就是让计算机用两个或多个相机来模仿这个过程,从而从2D图像中恢复出场景的3D深度信息。
2. 立体视觉的工作流程 (The Four Core Steps)
要从两张图像计算出深度,需要经过一个标准化的流程,通常分为以下四步:
第1步:相机标定 (Camera Calibration)
这是准备工作,目的是获取相机的“内部参数”和“外部参数”。
- 内参 (Intrinsics)
:描述相机自身的特性,如焦距
(fx, fy)、主点(cx, cy)(图像中心)和畸变参数。这些参数告诉我们相机如何将3D空间点投影到2D图像平面。 - 外参 (Extrinsics)
:描述两个相机之间的相对位置关系,即一个相机相对于另一个相机的旋转 (Rotation) 和平移 (Translation)。其中,两个相机中心之间的距离被称为基线 (Baseline),这是立体视觉中最重要的参数之一。
标定通常使用一个已知的图案(如棋盘格)来完成。
第2步:图像校正 (Image Rectification)
这是整个流程中最巧妙的一步,目的是简化匹配问题。
在未校正的原始图像中,左图中的一个点,它在右图中的对应点可能出现在任何位置,搜索起来非常困难。
图像校正通过对两张图像进行数学变换(投影变换),使得:
两张图像的成像平面完全共面。
两台相机的光心连线(基线)与成像平面平行。
两张图像的行是完全对齐的。
校正后的效果:左图中的任意一个点
(x, y),它在右图中的对应点必定位于同一行y上。这样,原本需要在整个2D图像中进行的搜索,就简化为了在一条直线上进行的一维搜索,极大地提高了匹配效率和精度。这条线被称为极线 (Epipolar Line)。第3步:立体匹配 (Stereo Matching / Correspondence)
这是立体视觉技术中最核心、最困难的一步。它的目标是为左图中的每一个像素,在右图的对应极线(同一行)上找到其匹配的像素。
挑战:
- 遮挡 (Occlusion)
:某个点只在一个相机中可见。
- 无纹理区域 (Textureless Regions)
:在一片白墙或纯色区域,所有像素看起来都一样,很难找到唯一的匹配。
- 重复纹理 (Repetitive Patterns)
:砖墙、栅栏等会产生很多相似的匹配候选,容易匹配错误。
- 遮挡 (Occlusion)
常用算法:
动态规划 (Dynamic Programming)
图割 (Graph Cuts)
置信度传播 (Belief Propagation)
SAD (Sum of Absolute Differences)
SSD (Sum of Squared Differences)
NCC (Normalized Cross-Correlation)
- 局部匹配算法 (Local Methods)
:速度快,是实时应用的主流。它以每个像素为中心,取一个小的窗口(Patch),然后在另一幅图像中寻找最相似的窗口。常用的相似性度量有:
- 全局匹配算法 (Global Methods)
:效果好,但计算量大。它不仅仅考虑局部窗口的相似性,还会引入平滑性等全局约束,将匹配问题看作一个整体的能量优化问题来求解。常用算法有:
第4. 步:深度计算 (Depth Calculation / Triangulation)
一旦我们成功地为像素
(x_L, y)找到了它在右图的匹配点(x_R, y),我们就可以计算出视差 (Disparity):d = x_L - x_R然后,利用相似三角形原理,我们可以计算出该点在三维空间中的深度
Z:Z = (f * B) / d其中:
Z是深度(距离)。
f是相机的焦距(来自内参)。
B是基线(两个相机光心之间的距离,来自外参)。
d是刚刚计算出的视差。
这个公式非常直观地揭示了立体视觉的本质:
- 视差
d越大,深度Z越小(物体越近)。 - 视差
d越小,深度Z越大(物体越远)。 - 基线
B越大,对于相同的深度,能测量的视差也越大,因此深度测量的精度越高。
对图像中的每个像素重复这个过程,我们就能得到一张深度图 (Depth Map),其中每个像素的值代表了其深度。
3. 优缺点分析
优点
- 被动式感知
:不向外界发射任何能量(如激光或红外光),隐蔽性好,不会相互干扰。
- 绝对尺度
:由于基线
B的长度是已知的物理量,立体视觉可以直接计算出物体的真实物理尺寸和距离,解决了单目视觉的尺度不确定性问题。 - 信息丰富
:除了深度,还能获取彩色、纹理信息。
- 成本相对较低
:相比于激光雷达,两个工业相机的成本要低很多。
缺点
- 匹配难题
:核心的立体匹配算法在遇到无纹理、重复纹理、反光、透明和遮挡区域时,性能会急剧下降。
- 基线限制
:
- 短基线
:适合近距离测量,但远距离精度差(因为视差太小)。
- 长基线
:适合远距离测量,但近距离视场重叠区小,且匹配更困难。
- 原理
- 计算量大
:尤其是全局匹配算法,对计算资源要求较高。
- 对光照敏感
:虽然比直接法SLAM好,但两个相机接收到的光照不一致会影响匹配效果。
4. 主要应用
- 机器人
:用于导航、避障、物体抓取。
- 自动驾驶
:作为感知系统的一部分,用于检测车辆、行人、障碍物的距离。
- 三维重建
:对物体或场景进行高精度的三维建模。
- 增强现实 (AR)
:理解真实世界的几何结构,以便正确放置虚拟物体。
- 无人机
:进行地形测绘和避障。
与其它3D传感器的对比
技术
原理
优点
缺点
立体视觉 被动式,三角测量
被动,可获绝对尺度,成本较低
匹配困难,受环境纹理和光照影响大
结构光 (RGB-D) 主动式,三角测量
精度高,不受环境纹理影响
室内使用,易受强光干扰,测量范围近
ToF (Time-of-Flight) 主动式,测量光飞行时间
响应快,不易受环境光干扰
精度相对较低,分辨率不高
激光雷达 (LiDAR) 主动式,测量激光飞行时间
精度极高,距离远,不受光照影响
成本高昂,无法获取颜色纹理,雨雪雾天气性能下降
总而言之,立体视觉是一种基础且强大的三维感知技术,它通过模拟人眼来理解世界,是许多智能系统“看懂”三维空间的关键。
4. 极线搜索与块匹配
我们来深入剖析立体视觉中最核心的两个操作:极线搜索 (Epipolar Search) 和 块匹配 (Block Matching)。
这两个概念紧密相连,共同解决了立体匹配中的两个基本问题:
- 去哪里找?(Where to search?)
—— 极线搜索 回答了这个问题。
- 哪个是最佳匹配?(How to find the best match?)
—— 块匹配 回答了这个问题。
1. 极线搜索 (Epipolar Search) —— 大幅缩小搜索范围
问题背景
想象一下,给你左相机拍的一张图,和右相机拍的一张图。让你在左图中随便选一个像素点
p,你如何在右图中找到它的“孪生兄弟”p'?最笨的办法是:在右图的整个二维平面上,一个像素一个像素地去比较,看看哪个跟
p最像。这个计算量是巨大的(复杂度为 O(宽 × 高)),对于实时应用来说是不可接受的。解决方案:利用极线几何 (Epipolar Geometry)
幸运的是,由于两个相机的位置是固定的,三维空间中的一个点
P、两个相机光心O_L,O_R、以及它在两个像平面上的投影p和p',它们之间存在着强大的几何约束。- 极平面 (Epipolar Plane)
:由
P,O_L,O_R三点构成的平面。 - 极线 (Epipolar Line)
:这个极平面与两个像平面的交线。
核心结论: 对于左图中的一个点
p,它在右图中的对应点p'必定位于右图中的那条极线上。这意味着,我们不再需要在整个右图中进行二维搜索,而只需要沿着这条一维的极线去搜索!搜索范围从一个面急剧缩小到一条线。
实际操作:图像校正 (Image Rectification)
虽然我们知道了要沿着极线搜索,但在原始图像中,极线通常是倾斜的,计算和搜索起来仍然不方便。
因此,在实际应用中,我们先进行图像校正。这个操作会对左右两张图像进行数学变换,使得:
- 所有极线都变成了水平的直线。
- 左图中的任意一条水平线,都与右图中同一高度的水平线一一对应。
最终效果:
对于左图中的像素(x_L, y),它在右图中的对应点(x_R, y)必然位于同一行y上。极线搜索就此被简化为“水平行搜索”,这是立体匹配能够高效实现的关键前提。
一句话总结极线搜索:通过利用相机的几何约束并将图像校正为水平对齐,它将寻找匹配点的二维搜索问题,降维成了一维的、沿着单条水平线的搜索问题。
2. 块匹配 (Block Matching) —— 如何判断相似性
现在我们知道了要在右图的某一行上寻找匹配点,但具体怎么判断“哪个点最像”呢?这就是块匹配要解决的问题。
为什么是“块”匹配,而不是“点”匹配?
单个像素只包含一个灰度值或颜色值,信息量太少,非常不具有区分度。在一片白墙上,所有像素点的值都一样,你根本无法匹配。
因此,我们不比较单个像素,而是比较以该像素为中心的一个小的矩形区域,这个区域被称为窗口 (Window)、块 (Block) 或 图像块 (Patch)。这个小区域包含了周围的纹理信息,使其更具独特性。
块匹配的步骤
假设我们要在左图的像素
p_L处寻找匹配。- 定义窗口
:在左图中,以
p_L为中心取一个N x N大小的窗口W_L(例如 7x7)。 - 滑动窗口
:在右图中,沿着与
p_L同一水平的极线,滑动一个同样大小的窗口W_R。 - 计算代价 (Cost Calculation)
:对于每一个可能的
W_R,计算它与W_L的“不相似程度”(即匹配代价)。代价越小,说明两个窗口越相似。 - 选择最佳匹配 (Winner-Takes-All, WTA)
:选择那个使匹配代价最小的窗口
W_R*。它的中心点p_R就被认为是p_L的最佳匹配点。
常用的匹配代价函数 (Cost Functions)
这些函数用来衡量两个图像块的相似度。
SAD (Sum of Absolute Differences) - 绝对差之和
- 原理
:逐个像素计算两个窗口中对应像素灰度值的差的绝对值,然后求和。
- 公式
:
Cost(W_L, W_R) = Σ |I_L(i,j) - I_R(i,j)| - 特点
:计算最简单,速度最快,是硬件实现的首选。对噪声比较敏感。
- 原理
SSD (Sum of Squared Differences) - 差的平方和
- 原理
:与SAD类似,但计算的是差的平方和。
- 公式
:
Cost(W_L, W_R) = Σ (I_L(i,j) - I_R(i,j))^2 - 特点
:对较大的差异给予更高的惩罚,因此对噪声和异常值更敏感。
- 原理
NCC (Normalized Cross-Correlation) - 归一化互相关
- 原理
:计算两个窗口的协方差,并用各自的标准差进行归一化。结果在
[-1, 1]之间,1表示完全相同,-1表示完全相反,0表示不相关。 - 公式
:比较复杂,但本质上是计算两个向量的余弦相似度。
- 特点
:对线性的光照和对比度变化具有很强的鲁棒性。如果右图比左图整体亮一些,SAD/SSD会得到很高的代价值,但NCC仍然能正确匹配。计算量比SAD/SSD大,但效果通常最好。
- 原理
总结:两者如何协同工作
- 输入
:两张经过相机标定和图像校正的左右图像。
- For 循环
:遍历左图中的每一个像素
p_L(x_L, y)。 - 极线搜索
:确定搜索范围是右图中的第
y行。 - 块匹配
:
a. 在左图p_L处取一个N x N的窗口W_L。
b. 在右图第y行,从左到右滑动一个同样大小的窗口W_R。
c. 对每个位置,使用SAD、SSD或NCC等代价函数计算Cost(W_L, W_R)。
d. 找到使代价最小(或NCC最大)的位置x_R。 - 计算视差
:
disparity = x_L - x_R。 - 输出
:得到一张视差图,其中每个像素的值就是它的视差。
极线搜索提供了高效的**“在哪里找”的策略,而块匹配提供了鲁棒的“如何确认”**的方法。它们是局部立体匹配算法的基石,也是理解更复杂全局匹配算法的基础。
5. 高斯分布的深度滤波器
这是一个非常深入和专业的问题。高斯分布的深度滤波器 (Gaussian Depth Filter) 是现代视觉SLAM(特别是半稠密或稠密SLAM)中用于稳健估计深度的核心技术之一。
我们来详细拆解这个概念。
1. 问题背景:为什么需要深度滤波器?
在立体视觉或运动恢复结构 (SfM) 中,我们通过三角化(Triangulation)来计算一个点的深度。这个过程通常只利用两个视角(例如,一个双目相机的左右图像,或者单目SLAM中的两个连续关键帧)。
这种基于两帧的深度估计存在严重问题:
- 噪声敏感
:像素匹配的微小误差(哪怕是亚像素级别)都可能导致深度计算的巨大偏差,尤其是在基线较短或物体较远的情况下。
- 歧义性
:在低纹理区域(如白墙)或重复纹理区域,立体匹配本身就非常不可靠,容易产生错误的匹配和离谱的深度值。
- 不确定性
:单次测量无法告诉我们这个深度估计到底有多可靠。
核心思想:不要相信任何一次单独的深度测量。我们应该融合来自多个视角的观测信息,随着观测次数的增加,逐步提炼出一个更准确、更可靠的深度值。深度滤波器就是实现这一目标的优雅方法。
2. 核心概念:用高斯分布来描述深度
深度滤波器的精髓在于,它不再将一个像素的深度看作一个确定的值(例如
Z = 2.5米),而是将其建模为一个一维高斯分布(正态分布)N(μ, σ²)。- 均值 (μ)
:代表当前对深度的最佳估计值。
- 方差 (σ²)
:代表该深度估计的不确定性。
- σ² 很大
:表示我们对这个深度值非常不确定,它可能在很大范围内波动(一个又宽又扁的钟形曲线)。
- σ² 很小
:表示我们对这个深度值非常有信心,它非常接近于均值μ(一个又窄又尖的钟形曲线)。
- σ² 很大
这种表示方法带来了巨大的好处:它将“不确定性”这个概念量化了,为后续的贝叶斯融合提供了数学基础。
3. 深度滤波的工作流程:贝叶斯更新
深度滤波器是一个**递归(Recursive)**的过程,就像卡尔曼滤波器一样。它遵循一个“预测-更新”或在这里更贴切的“初始化-更新”循环。
假设我们想为关键帧 A 中的一个像素
p估计深度。第1步:初始化 (Initialization)
当像素
p第一次被选为深度估计的候选点(我们称之为“种子点”)时,我们对它的深度一无所知。我们会给它一个初始的深度分布
N(μ_init, σ²_init)。μ_init可以是一个预设的平均深度,或者通过一个粗略的两帧匹配得到。
σ²_init会被设置成一个非常大的值,表示极高的不确定性。
第2步:获取新观测 (Get a New Observation)
相机移动后,我们得到了一个新的观测帧 B。我们已经通过VSLAM前端知道了帧A和帧B之间的相对位姿。
- 极线搜索
:我们在观测帧B中,沿着像素
p对应的极线进行搜索,找到它的匹配点p'。 - 三角化
:利用
p、p'和两帧的位姿,我们计算出一个新的深度测量值d_obs。 - 为观测建模不确定性
:这次观测本身也是不完美的。它的不确定性
σ²_obs主要来源于极线搜索的匹配精度。通常,匹配窗口的NCC(归一化互相关)得分越高,σ²_obs就越小。
现在,我们有了一个新的“证据”:一个带有不确定性的深度测量
N(d_obs, σ²_obs)。第3步:融合/更新 (Fusion / Update)
这是整个滤波器的核心。我们要将先验知识(Prior)
N(μ_prior, σ²_prior)和新的观测(Measurement)N(d_obs, σ²_obs)融合,得到一个更新后的后验知识(Posterior)N(μ_post, σ²_post)。根据贝叶斯理论,两个高斯分布的乘积(在概率意义上)仍然是一个高斯分布。其新的均值和方差可以通过以下公式计算:
新的均值
μ_post:μ_post = (σ²_obs * μ_prior + σ²_prior * d_obs) / (σ²_prior + σ²_obs)新的方差
σ²_post:σ²_post = (σ²_prior * σ²_obs) / (σ²_prior + σ²_obs)
对公式的直观理解:
新的均值是旧的均值和新观测值的加权平均。权重由对方的方差决定。如果新观测非常可靠(
σ²_obs很小),它就会在新的均值中占有更大的比重。新的方差总是小于之前的方差和观测的方差。这意味着每一次有效的融合都会让我们的估计变得更加确定。
第4. 步:迭代与收敛
我们带着更新后的后验分布
N(μ_post, σ²_post),等待下一个观测帧 C 的到来,然后重复第2步和第3步。- 离群点剔除
:在融合之前,需要检查新的观测值
d_obs是否是离群点。如果d_obs离当前的均值μ_prior太远(例如超过了3个标准差3σ_prior),我们就认为这是一次错误的匹配,直接丢弃它,不进行更新。 - 收敛判断
:当一个像素的深度方差
σ²经过多次更新后,减小到一个预设的阈值以下时,我们就认为这个点的深度已经收敛 (Converged)。此时,我们可以认为它的均值μ是一个稳定可靠的深度值,并将其正式作为一个3D地图点固化下来。
一个生动的比喻:专家会诊
- 像素
p:一个疑难杂症病人。
- 深度分布
N(μ, σ²):专家组对病情的当前诊断(
μ)和分歧程度(σ²)。 - 初始状态
:专家组刚成立,对病情只有一个大概猜测,分歧巨大(
μ不准,σ²很大)。 - 新观测帧
:一位新的外来专家(可能是个影像科医生),他对病情给出了自己的诊断
d_obs和自信程度σ²_obs。 - 融合过程
:专家组开会讨论,综合了已有意见和新专家的意见。新专家如果非常权威(
σ²_obs小),他的话语权就重。 - 结果
:会议后,专家组得出了新的共识
μ_post,并且内部分歧减小了(σ²_post变小)。 - 收敛
:经过多位不同科室的专家会诊后,专家组对病情的诊断高度一致(
σ²足够小),可以下最终诊断结论了。
优势与应用
- 鲁棒性强
:能够有效滤除单次测量的噪声和离群点。
- 处理不确定性的优雅框架
:提供了一种符合概率论的、原则性的方式来融合信息。
- 提高精度
:通过融合多个(通常是宽基线)的观测,最终得到的深度精度远高于任何单次两帧测量。
这种技术是半稠密SLAM(如SVO)和一些稠密SLAM方法的核心组成部分,它使得在只使用单目相机的情况下,也能生成相当准确和密集的深度图,为高质量的三维重建奠定了基础。
6. 均匀-高斯混合分布的深度滤波器
这是一个比单纯高斯滤波器更进一步、更鲁棒的方案。我们来深入探讨均匀-高斯混合分布的深度滤波器 (Uniform-Gaussian Mixture Depth Filter)。
这个模型主要由 DSO (Direct Sparse Odometry) 的作者在其后续的稠密建图工作中提出和推广,旨在解决标准高斯深度滤波器的一些局限性。
1. 为什么要从“高斯”升级到“均匀-高斯”?
标准的高斯深度滤波器有一个隐含的假设:我们的深度估计虽然有误差,但总体上是围绕着一个真实值波动的。换句话说,它能很好地处理“噪声”,但很难处理“完全错误”的初始情况。
考虑一个棘手场景:
假设你正在对一个低纹理区域(比如一面白墙)的像素进行深度估计。
- 错误的初始化
:由于缺乏纹理,你的第一次两帧匹配可能完全是随机的,给出了一个离谱的深度初始值
μ_init。 - 高斯滤波器的困境
:虽然你给这个初始值分配了一个很大的方差
σ²_init,但后续的观测如果也因为低纹理而匹配错误,但“碰巧”落在了μ_init ± 3σ的范围内,它们就会被错误地融合进去。更糟糕的是,一个真正正确的观测值,如果离这个错误的μ_init太远,反而会被当作离群点而被拒绝掉! - 结果
:滤波器可能会收敛到一个完全错误的深度值上,并且还“自信地”认为自己的方差很小。
核心问题:标准高斯模型只有一个“峰”,它无法同时表示“我可能在这里,但也可能在完全别的地方”这种模棱两可的状态。
2. 均匀-高斯混合分布模型
为了解决这个问题,我们引入一个更复杂的概率模型来描述深度
d的不确定性:p(d) = π * U(d_min, d_max) + (1 - π) * N(μ, σ²)这个模型由两部分组成,通过一个混合权重
π(pi) 连接:均匀分布 (Uniform Distribution)
U(d_min, d_max):- 含义
:代表了“完全不知道”的状态。它认为深度值在某个非常大的范围
[d_min, d_max]内(例如从0.1米到10米)是等可能的。 - 作用
:捕获那些完全离谱的、随机的匹配结果。它像一个“安全网”,表示我们对深度值还没有任何可靠的线索。
- 含义
高斯分布 (Gaussian Distribution)
N(μ, σ²):- 含义
:与之前一样,代表了一个“有根据的猜测”。它认为深度值很可能在
μ附近,其不确定性由σ²描述。 - 作用
:当我们收集到一些一致的观测后,这个高斯部分就会逐渐“成长”起来,形成一个尖峰。
- 含义
混合权重
π(0 ≤ π ≤ 1):- 含义
:表示深度值属于“均匀分布”(即完全未知)的概率。
π接近 1:意味着我们几乎完全不确定深度在哪里,主要由均匀分布主导。这是滤波器的初始状态。
π接近 0:意味着我们非常有信心深度就在高斯分布描述的位置附近。这是滤波器收敛后的状态。
- 含义
3. 均匀-高斯深度滤波的工作流程
这个滤波器的更新流程比纯高斯滤波器更复杂,因为它需要同时更新
π,μ,σ²这三个参数。第1步:初始化
π被初始化为一个接近 1 的值(例如 0.99),表示我们处于完全不确定的状态。
高斯部分
N(μ, σ²)的初始值可以随意设置,因为它的权重(1 - π)此时几乎为零,不起作用。均匀分布的范围
[d_min, d_max]是预先设定的。
第2步:获取新观测
和之前一样,我们从一个新的观测帧中,通过极线搜索和匹配,得到一个带不确定性的新观测
d_obs,其概率分布为p_obs(d) = N(d_obs, σ²_obs)。第3步:贝叶斯更新(核心步骤)
我们要计算后验分布
p_post(d) ∝ p_prior(d) * p_obs(d)。将先验
p_prior(d) = π_prior * U + (1 - π_prior) * N_prior和观测p_obs(d) = N_obs代入相乘,会得到一个复杂的形式。为了使其变回“均匀-高斯”的形式,需要进行近似和参数更新。这个过程可以分解为:
计算观测属于两个模式的概率:
- 观测与均匀分布的“匹配度”
L_U:计算
N_obs与U的重叠程度。因为U是平的,所以这基本上是一个常数。 - 观测与高斯分布的“匹配度”
L_G:计算
N_obs与N_prior的重叠程度。这个可以通过计算两个高斯分布乘积的积分来得到。它衡量了新观测与我们旧的“最佳猜测”有多么吻合。
- 机器人
更新混合权重
π:
新的π_post是旧的π_prior与两个匹配度的加权组合。π_post ∝ π_prior * L_U
(同时(1 - π_post)也与(1 - π_prior) * L_G成正比,最后需要归一化)- 直观理解
:如果新观测与旧的高斯峰
N_prior吻合得很好(L_G大),那么(1 - π)的权重就会增加,π就会减小,意味着我们对高斯峰更有信心了。反之,如果观测与高斯峰相差甚远,π的权重会相对增加。
- 直观理解
更新高斯分布
N(μ, σ²):
高斯部分的更新只使用那些更可能属于高斯模式的观测。首先,将旧的高斯
N_prior与新的观测N_obs相乘,得到一个中间态的高斯N_intermediate。然后,新的高斯均值
μ_post和方差σ²_post是旧的μ_prior和这个中间态μ_intermediate的加权平均,权重由L_G等因素决定。
第4. 步:收敛与固化
- 收敛判断
:当
(1 - π)足够大(即π足够小) 并且 高斯部分的方差σ²也足够小时,我们才认为深度已经收敛。 这个双重条件比单纯的
σ²判断要严格得多,它确保了我们不仅是“精确”的,而且是“确定地精确”,排除了收敛到错误值的可能性。
优势总结
- 极强的鲁棒性
:通过引入均匀分布,滤波器能够很好地处理初始化模糊性和严重的离群点。它给了系统一个“反悔”和“重新开始寻找”的机会。
- 更可靠的收敛
:只有当足够多的一致性观测使得高斯部分从均匀背景中“脱颖而出”时,滤波器才会收敛。这有效避免了在低纹理区域收敛到错误深度的问题。
- 更真实的建模
:均匀-高斯混合模型比单一高斯模型更能描述现实世界中深度估计的不确定性状态。
缺点:
- 计算更复杂
:需要维护和更新更多的参数。
- 参数调整
:需要额外调整
π的初始值和收敛阈值等超参数。
总而言之,均匀-高斯混合深度滤波器是标准高斯深度滤波器的进化版,它通过一个更复杂的概率模型,极大地增强了深度估计算法在挑战性场景(尤其是低纹理和初始化阶段)下的鲁棒性,是构建高质量稠密/半稠密地图的关键技术之一。
7.逆深度
我们来详细讲解一个在视觉SLAM中非常巧妙且重要的概念——逆深度 (Inverse Depth)。
这个概念的提出,主要是为了解决传统深度表示法在处理远处点和不确定性时遇到的数值问题。
1. 传统深度表示法的问题
在标准的SLAM系统中,一个三维空间点通常用其在某个相机坐标系下的坐标
P = (X, Y, Z)来表示。其中Z就是深度 (Depth)。这种表示方法在大多数情况下都很好用,但有两个主要问题:
问题一:无法表示无穷远的点
想象一个位于无穷远的点,比如天空中的一个像素。它的深度
Z是无穷大(∞)。在计算机中,我们无法用一个浮点数来精确表示无穷大。
更重要的是,在进行数学优化(如后端优化)时,一个无穷大的值会导致计算上的奇异性 (Singularity) 和数值不稳定。这使得基于高斯分布的状态估计(如卡尔曼滤波或图优化)变得非常困难甚至不可能。
问题二:深度不确定性的非高斯性
在视觉SLAM中,我们通常假设状态变量(如相机位姿、地图点坐标)的不确定性服从高斯分布。这是因为高斯分布有很多优良的数学性质,便于进行滤波和优化。
然而,对于一个通过三角化测量得到的深度
Z,它的不确定性并不服从高斯分布。- 直观理解
:
对于一个近处的点,一个小的视差误差
Δd对应一个小的深度误差ΔZ。对于一个远处的点,同样的视差误差
Δd会导致一个巨大的深度误差ΔZ。这导致深度的概率密度函数(PDF)是一个“拖着长长尾巴”的形状,特别是对于远处点,它严重偏离对称的高斯分布。如果强行用高斯分布去近似它,会产生很大的模型误差。
2. 逆深度的定义与优势
为了解决上述问题,研究者们提出了逆深度参数化 (Inverse Depth Parametrization)。
定义:
逆深度ρ(rho) 就是深度的倒数:ρ = 1 / Z一个三维点
P不再由(X, Y, Z)表示,而是由它在第一次被观测到的相机坐标系下的方向向量和逆深度来共同描述。具体来说,一个点可以由一个6维向量表示:p = (x_ref, y_ref, z_ref, θ, φ, ρ)
其中:(x_ref, y_ref, z_ref)是该点第一次被观测时,相机的位置。
(θ, φ)是从该相机位置指向该点的方向角(方位角和俯仰角)。
ρ是该点沿此方向的逆深度。
逆深度的三大优势
优雅地表示无穷远:
当一个点位于无穷远时,
Z → ∞。此时,它的逆深度
ρ = 1/Z → 0。- 零是一个完美的、良性的浮点数
。我们可以毫无问题地初始化一个点的逆深度为0,表示它可能在无穷远。这解决了传统深度表示的奇异性问题。
使不确定性更接近高斯分布:
神奇的是,当我们将不确定性从深度
Z空间映射到逆深度ρ空间时,原本非高斯的分布变得非常接近高斯分布了。从
Z = (f * B) / d和ρ = 1/Z = d / (f * B)可以看出,逆深度ρ与视差d是线性关系。我们通常假设像素测量误差(即视差误差
Δd)是服从高斯分布的。由于ρ和d是线性关系,所以ρ的不确定性也近似服从高斯分布。这使得我们可以放心地在逆深度上使用基于高斯假设的滤波器(如EKF)和优化器,大大提高了算法的稳定性和精度。
处理“可能在相机后面”的点:
在三角化的过程中,由于噪声,有时计算出的点可能位于相机的“后面”(即
Z为负)。这在物理上是不可能的,但在计算中可能发生。传统深度
Z在从正到负跨越0时会产生奇异性。而逆深度
ρ = 1/Z可以平滑地从一个正值(Z > 0)通过无穷大(Z接近+0)/负无穷大(Z接近-0)过渡到一个负值(Z < 0)。这意味着,即使一个点被错误地初始化到相机后面,滤波器也可以在后续的更新中,平滑地将其“拉”回到相机前面,而不会导致数值崩溃。这增加了系统的鲁棒性。
3. 应用场景
逆深度参数化在很多经典的VSLAM算法中都扮演了关键角色,尤其是在单目SLAM中。
滤波方法 (EKF-based SLAM):
在经典的 MonoSLAM 中,地图中的点就是用逆深度来表示的。当一个新的特征点被检测到时,它的状态被初始化为一个逆深度值(可能是0)和很大的不确定性。随着相机移动和不断的观测,EKF会更新这个逆深度值及其不确定性。
半稠密/稠密SLAM:
在 LSD-SLAM 或 DSO 及其后续的稠密建图工作中,深度滤波器(无论是高斯还是均匀-高斯)通常都是在逆深度空间中进行的。这样做的好处是,可以统一处理从近到远的所有像素,并且概率模型更符合高斯假设。
初始化阶段:
对于单目SLAM,在系统刚启动,基线非常短的时候,深度估计的误差极大。使用逆深度可以稳定地处理这种巨大的不确定性,直到相机移动了足够长的距离,深度才被可靠地估计出来。
总结
逆深度不是一种新的物理量,而是一种更聪明的数学参数化技巧。它通过一个简单的求倒数操作,解决了传统深度表示法在处理无穷远点和深度不确定性时的数值和概率模型问题。
特性
传统深度 (Z)
逆深度 (ρ = 1/Z)
无穷远点 Z = ∞(数值不稳定)
ρ = 0(数值稳定)
不确定性分布 非高斯
近似高斯
处理相机后方点 跨越0时奇异
平滑过渡
主要优点 直观
数学性质优良,鲁棒性强
在现代VSLAM算法中,尤其是在需要精细处理不确定性的滤波方法和稠密建图方法中,使用逆深度已经成为了一种标准实践。它体现了在解决工程问题时,选择正确的数学表示是多么重要。
8.块匹配前图像间的变换
这是一个非常核心的问题,它直指立体视觉效率和准确性的关键。在进行块匹配(Block Matching)之前,对原始图像对进行一系列精心设计的变换是必不可少的步骤。
这个核心变换的名称叫做图像校正 (Image Rectification),但它依赖于更基础的预处理。
我们来分解一下整个流程:
目标:将复杂的二维搜索降维成简单的一维搜索
在块匹配中,我们的任务是:为左图中的一个像素点,在右图中找到它的同名点。
- 没有变换的“蛮力”方法
:在原始图像中,左图的一个点,其同名点可能出现在右图的任何位置。我们需要在整个二维图像中进行搜索,计算量巨大,效率极低。
- 利用几何约束
:幸运的是,我们有极线几何 (Epipolar Geometry) 这个强大的约束。它告诉我们,左图的一个点,其在右图的同名点必定位于一条称为极线 (Epipolar Line) 的直线上。这已经将搜索范围从一个面缩小到了一条线。
- 变换的终极目标
:但是,在原始图像中,这些极线通常是倾斜的,并且左右图像中的极线不一定在同一高度。这对于计算机程序来说仍然不方便。因此,我们需要一个变换,使得所有极线都变成水平的,并且左右图像中对应的极线位于同一行。
实现这个终极目标的变换,就是图像校正。
块匹配前的变换流程
这个流程可以分为两个主要阶段,共三个关键步骤。
阶段一:获取变换所需的信息
在进行任何变换之前,我们必须先了解相机的“身份信息”。
步骤 1: 相机标定 (Camera Calibration)
这是所有变换的基础。通过拍摄一个已知的标定板(如棋盘格),我们可以计算出:
- 相机内参 (Intrinsics)
:
焦距
(fx, fy)主点
(cx, cy)(光心在图像平面上的投影)- 畸变系数 (Distortion Coefficients)
:描述由真实镜头不完美性引起的图像失真。
- 相机外参 (Extrinsics)
:
- 旋转矩阵 R
和 平移向量 T:描述右相机相对于左相机的空间位置关系。这是进行立体校正的最关键信息。
- 旋转矩阵 R
阶段二:应用几何变换
有了相机的内外参数后,我们就可以对图像进行实际的几何变换了。
步骤 2: 图像去畸变 (Image Undistortion)
这是第一个应用的变换。真实世界的镜头都不是完美的针孔模型,会产生图像畸变,最常见的是径向畸变(枕形或桶形失真)和切向畸变。
- 目的
:消除这些畸变,使得图像中的直线就是真正的直线,恢复一个理想的针孔相机模型下的图像。
- 方法
:利用标定得到的畸变系数,对图像中的每一个像素点进行位置重映射,将其移动到它“应该在”的无畸变位置。
注意:去畸变是后续所有几何变换(包括校正)的前提,因为它确保了极线几何的假设成立。
步骤 3: 图像立体校正 (Stereo Rectification)
这是最核心的变换,它在去畸变的基础上进行。
目的:对左右两张图像进行投影变换(在数学上是一个单应性变换 Homography),使得变换后的图像对满足以下理想条件:
两幅图像的成像平面完全共面。
两幅图像的行是完全对齐的,即所有极线都是水平的。
左图中的任意点
(x, y),其在右图的同名点必然位于同一水平扫描线y上。垂直方向上的视差为零。
方法:
利用标定得到的外参
R和T,计算出一对新的旋转矩阵R_left和R_right。这两个矩阵会“虚拟地”旋转左右相机,使它们的光轴平行,基线与成像平面平行。根据新的旋转矩阵和原始的相机内参,可以为左右图像分别计算一个重映射查找表 (Remapping Map)。
使用这个查找表,通过插值(如双线性插值)的方式,从原始(或已去畸变)的图像中生成新的、已校正的图像。
在OpenCV等库中,
stereoRectify()函数负责计算这些变换矩阵,而initUndistortRectifyMap()和remap()函数负责执行实际的去畸变和校正变换。总结
一句话总结:块匹配前的变换,主要是指图像校正,它通过去畸变和投影变换,将一个困难的、不规则的二维搜索问题,转化成了一个简单的、沿水平线的一维搜索问题,极大地提升了立体匹配的速度和可靠性。
9.RGB-D稠密建图
我们来详细探讨RGB-D稠密建图。这是一个在视觉SLAM领域中相对成熟且效果显著的技术分支。
相比于需要复杂算法来估计深度的单目或双目SLAM,RGB-D SLAM的起点就要高很多,因为它直接拥有了深度信息。
1. 什么是RGB-D稠密建图?
- RGB-D
:指的是传感器能同时提供两种数据:
- RGB图像
:标准的彩色图像,提供丰富的纹理和颜色信息。
- 深度图像 (Depth Image)
:一张灰度图,其中每个像素的灰度值直接对应于该点到相机的距离(深度)。
- RGB图像
- 稠密建图 (Dense Mapping)
:目标是利用这些数据,构建出一个包含场景中绝大部分几何细节的三维模型,而不仅仅是稀疏的特征点。
核心优势:由于深度信息是直接测量的,而不是像单目/双目那样需要通过复杂的匹配和计算来估计,所以RGB-D稠密建图在原理上更简单,计算效率更高,且生成的模型通常更完整。
常用RGB-D相机:
- 结构光 (Structured Light)
:如第一代Kinect、Orbbec Astra。通过向场景投射已知的红外散斑图案,然后根据图案的形变来计算深度。
- 飞行时间 (Time-of-Flight, ToF)
:如Kinect v2、一些现代手机的LiDAR传感器。通过测量红外光脉冲从发射到接收的时间差来计算距离。
2. RGB-D稠密建图的主流技术流程
目前,最经典、最高效的RGB-D稠密建图方法是基于体素融合 (Voxel Fusion) 的,其代表性工作是 KinectFusion (由微软研究院在2011年提出) 及其后续的无数改进。
这个流程可以概括为“定位 -> 融合 -> 提取”三部曲。
第1步:相机位姿跟踪 (Camera Pose Tracking)
这是整个系统的“前端”。我们需要实时地计算出每一帧RGB-D数据被采集时,相机在世界坐标系中的精确位姿
T_wc(从相机到世界的变换)。主流方法:ICP (Iterative Closest Point) 算法及其变种
- 点到面 (Point-to-Plane) ICP
:比传统的点到点ICP更精确、收敛更快。它最小化的是点到其对应点所在平面的距离。
- 结合RGB信息
:在查找对应点和优化时,同时考虑几何距离和颜色相似度,可以提高在几何特征不明显但纹理丰富区域的跟踪精度。
- 查找对应点 (Correspondence)
:为当前帧点云中的每个点,在模型中找到最近的点。
- 计算变换 (Compute Transformation)
:计算一个能最小化所有对应点对之间距离的刚体变换(旋转+平移)。
- 应用变换 (Apply Transformation)
:将计算出的变换应用到当前帧的位姿上。
- 迭代
:重复以上步骤,直到变换收敛(变化足够小)。
当前帧的点云(通过深度图和相机内参计算得到)。
上一帧或全局模型生成的“虚拟”点云/表面。
- 点到面 (Point-to-Plane) ICP
- 输入
:
- 过程
:ICP是一个迭代优化过程。
- 变种
:
输出:当前帧精确的相机位姿
T_wc。第2步:体素融合与更新 (Voxel Fusion and Update)
这是系统的“后端”和“建图”核心。它负责将一帧一帧的深度数据,融合到一个统一的、全局的三维模型中。
核心数据结构:TSDF (Truncated Signed Distance Function)
如之前在单目稠密重建中提到的,这是目前最主流的融合方法。我们将整个三维空间划分成一个巨大的体素网格 (Voxel Grid)。每个体素存储两个值:
"Truncated"(截断)意味着我们只在物体表面附近的一小段区域内(截断带)精确计算和存储SDF值,离表面太远的体素直接赋一个最大/最小值,以节省内存和计算。
- SDF值 (Signed Distance)
:该体素中心到最近物理表面的有符号距离。在物体内部为负,外部为正,表面为零。
- 权重 (Weight)
:表示该SDF值估计的置信度。观测次数越多,权重越高。
融合过程 (Fusion Process):
对于当前帧的每一个像素,利用其深度值
d和刚刚计算出的相机位姿T_wc,将其反向投影到全局的TSDF体素网格中。这个投影会形成一条射线 (Ray)。我们遍历这条射线路径上、位于相机视锥内且在截断带范围内的所有体素。
对于每一个被遍历到的体素,我们计算它与真实表面点之间的距离(这就是当前帧对该体素SDF值的测量),然后通过加权平均的方式,更新该体素中存储的SDF值和权重。
SDF_new = (W_old * SDF_old + W_curr * SDF_curr) / (W_old + W_curr)W_new = W_old + W_curr通过不断地重复这个过程,来自不同视角的观测会被不断地平均。噪声点因为不一致性会被平滑掉,而真实的表面因为被多次一致地观测而得到加强,最终形成一个平滑、精确、完整的隐式表面模型。
第3步:表面提取与可视化 (Surface Extraction and Visualization)
TSDF本身只是一个存储在内存中的数据结构,为了得到可视化的三维模型,我们需要从中提取出表面网格。
常用算法:移动立方体 (Marching Cubes)
该算法遍历TSDF体素网格中的每一个小立方体(由8个体素构成)。通过检查8个顶点的SDF值的正负号,可以判断表面(SDF=0的等值面)是如何穿过这个立方体的。然后,根据预先定义好的模板,生成对应的小三角面片。实时可视化:光线投射 (Ray Casting)
在实时建图过程中,我们通常不会每一帧都运行昂贵的Marching Cubes。取而代之的是,从当前虚拟相机的视角,向TSDF体素网格中发射射线。通过步进的方式找到射线与SDF=0表面的交点,并根据交点处的法向量(通过SDF梯度计算)进行光照计算,从而实时渲染出当前视角下的模型表面。这个渲染出的图像还可以用于下一帧的ICP跟踪。
3. 优缺点与挑战
优点
- 高效率和高完整性
:由于深度已知,避免了复杂的匹配搜索,可以直接进行几何融合,速度快,且能构建出非常完整的模型。
- 鲁棒性强
:对场景纹理要求低,即使在白墙等区域也能很好地工作。
- 技术成熟
:以KinectFusion为代表的框架非常成熟,有大量开源实现(如PCL, Open3D, InfiniTAM)。
缺点与挑战
传感器限制:
- 测量范围有限
:消费级RGB-D相机的有效测距通常在0.5米到4-5米之间,不适合大场景建图。
- 对材质和环境敏感
:对黑色(吸光)、透明、反光表面会失效。在室外强光下,红外传感器会受到严重干扰。
累积误差与回环检测:
基于ICP的帧到模型跟踪会不可避免地产生累积误差。如果相机绕了一圈回到原点,地图可能会出现错位。
因此,现代的RGB-D SLAM系统通常会加入回环检测 (Loop Closing) 模块(通常基于RGB图像的词袋模型),在检测到回环时进行全局位姿图优化 (Pose Graph Optimization),来修正整个轨迹和地图。
内存和计算消耗:
- 哈希体素 (Voxel Hashing)
:如InfiniTAM所用,只在实际有表面的地方分配内存,而不是为一个巨大的固定网格预先分配,极大地节省了内存。
- 地图滚动/子图 (Submapping)
:只在相机周围的一块活动区域维护高分辨率地图,当相机移走后,将旧的地图数据压缩或保存到硬盘。
TSDF体素网格非常消耗内存。一个高分辨率的大场景模型可能需要几GB甚至几十GB的内存。
- 解决方案
:
- 哈希体素 (Voxel Hashing)
动态物体:场景中的移动物体会破坏静态世界的假设,可能在地图上留下“鬼影”或错误的几何结构。需要动态物体检测与分割算法来剔除它们。
4. 总结
RGB-D稠密建图是一种强大而实用的技术,它通过ICP位姿跟踪和TSDF体素融合两大核心技术,能够高效地构建出高质量、高完整性的三维环境模型。虽然它受到传感器的物理限制,但在室内、中小型场景下的应用中表现极其出色,是机器人导航、AR/VR、三维扫描等领域的关键技术。未来的发展方向包括与深度学习结合以实现更好的语义理解、动态物体处理以及在大规模场景下的高效建图。
10. 点云重建网格
我们来详细探讨一下“点云重建网格”这个话题。这是一个在3D计算机视觉、计算机图形学和逆向工程中至关重要的步骤。
核心任务:将一堆离散、无序的三维点(点云)转换成一个由顶点、边和面构成的连续表面模型(通常是三角网格,即Mesh)。
为什么需要这个转换?
点云本身只是点的集合,虽然能表示物体的形状,但缺乏拓扑结构和表面信息。而网格模型:- 可视化效果更好
:可以进行平滑着色、光照和纹理贴图。
- 几何计算更方便
:可以轻松计算体积、表面积、曲率等。
- 应用范围更广
:可用于3D打印、物理仿真、游戏、动画和CAD/CAM。
点云重建网格的主要方法
重建方法多种多样,可以根据其数学原理大致分为以下几类。选择哪种方法取决于点云的质量(是否有序、有无法线、噪声水平)和应用需求(速度、精度、水密性)。
1. 基于三角剖分的方法 (Triangulation-based)
这类方法直接在点云的投影或空间关系上构建三角形。
a) 2.5D Delaunay 三角剖分 (2.5D Delaunay Triangulation)
- 适用场景
:主要用于从单个深度图或LiDAR扫描生成的有序点云 (Organized Point Cloud),类似于一个高度场。
- 原理
:
将所有三维点
(x, y, z)投影到(x, y)二维平面上。对这些二维点进行Delaunay三角剖分。Delaunay三角剖分有一个很好的性质:任何一个三角形的外接圆内部都不包含其他的点。这通常会产生“形态良好”的三角形,避免了狭长形状。
将二维平面上的三角形连接关系,映射回原始的三维点,从而形成三维网格。
- 可视化效果更好
- 优点
:速度极快,算法简单。
- 缺点
:只适用于类似于地形的高度场数据,无法处理复杂的、有悬垂或闭合的物体。生成的网格可能存在不符合真实表面的“长边”三角形。
b) 3D Delaunay 三角剖分 / Alpha Shapes
- 适用场景
:无序点云。
- 原理
:
alpha很大:结果接近点云的凸包。
alpha很小:结果可能产生很多孔洞,甚至断开。
对所有三维点进行3D Delaunay三角剖分。结果不是一个表面,而是一堆填充了整个点云凸包的四面体 (Tetrahedron)。
- Alpha Shapes 算法
:通过一个名为
alpha的参数来“雕刻”这些四面体。它会移除那些外接球半径大于alpha的四面体。 alpha值控制了重建的细节程度:
通过选择一个合适的
alpha值,可以从四面体集合中提取出代表物体表面的三角形面片。
- 适用场景
- 优点
:有严格的数学定义,能处理任意拓扑结构。
- 缺点
:对
alpha参数的选择非常敏感,且难以自动确定最佳值。容易在点云稀疏区域产生孔洞。 2. 基于隐式函数的方法 (Implicit Function-based)
这类方法是目前最主流、效果最好的方法。它们不直接连接点,而是先定义一个隐式的三维函数
f(x, y, z),使得物体的表面是f(x, y, z) = 0的等值面。a) 移动立方体 (Marching Cubes)
这是从隐式函数中提取网格的标准算法。
- 前提
:你需要一个定义在三维空间网格(体素)上的标量场,即每个体素顶点都有一个函数值。
- 原理
:
将空间划分为一个规则的体素网格。
遍历每个小立方体(体素)。
检查立方体的8个顶点的函数值是正还是负。
根据这8个值的正负组合(共256种情况),可以确定等值面是如何穿过这个立方体的。
从一个预计算的查找表中,获取构成表面的三角形顶点和连接关系。
将所有立方体生成的三角面片拼接起来,形成最终的网格。
b) 泊松表面重建 (Poisson Surface Reconstruction)
这是高质量表面重建的黄金标准之一。
- 核心思想
:将表面重建问题看作一个求解泊松方程的过程。它假设点云的法向量是指向物体内部或外部的。
- 原理
:
- 需要法向量
:算法的输入不仅是点的位置,还必须有每个点的法向量。如果点云没有法向量,需要先进行法线估计(例如通过分析邻近点的PCA)。
- 定义指示函数
:构建一个指示函数
χ,在物体内部为1,外部为0。这个函数的梯度在表面附近就等于我们输入的法向量场。 - 求解泊松方程
:求解
∇²f = ∇·v(其中v是法向量场)。这个方程的解f就是我们想要的隐式函数。 - 提取表面
:在求解得到的标量场
f上运行移动立方体算法,提取出f(x, y, z) = c的等值面。
- 前提
- 优点
:
- 鲁棒性强
:对噪声不敏感,能很好地处理噪声和不均匀采样的点云。
- 水密性好
:倾向于生成封闭的、没有孔洞的(水密的)模型。
- 重建质量高
:表面非常平滑。
- 鲁棒性强
- 缺点
:
- 需要法向量
,且法向量的方向必须一致(都朝内或都朝外)。错误的法向量会产生严重的错误。
倾向于平滑掉尖锐的特征和细节。
计算量较大。
c) 径向基函数 (Radial Basis Functions, RBF)
- 原理
:使用一系列以点云中的点为中心的径向基函数(如高斯函数)的线性组合来定义隐式函数。通过求解一个线性方程组来确定每个函数的权重,使得在所有点云样本上函数值为0。
- 优点
:可以很好地插值数据,能保留细节。
- 缺点
:当点云规模很大时,求解线性方程组的计算成本非常高。
3. 基于点云投影与图论的方法
a) 贪婪投影三角化 (Greedy Projection Triangulation)
- 适用场景
:具有较好法线信息的点云。
- 原理
:这是一个类似“滚雪球”的贪心算法。
从一个点开始,连接它最近的邻居,形成第一个三角形。
不断地沿着已有网格的边界,寻找可以形成“好”三角形(例如,角度不太小,法线与点法线一致)的下一个点,并将其连接进来,逐步扩展网格。
这个过程就像一个雪球在滚动中不断粘上新的雪花。
- 需要法向量
- 优点
:速度较快,能较好地保留细节,直观易懂。
- 缺点
:是局部算法,无法保证全局的最优性或水密性。在点云密度变化大或噪声多的区域容易失败。
方法选择指南
方法类型
适用场景
优点
缺点
推荐算法
2.5D 三角剖分 有序点云、高度场
速度极快
无法处理复杂拓扑
2.5D Delaunay
3D 三角剖分 需要保留所有原始点
数学定义清晰
对参数敏感,易产生孔洞
Alpha Shapes
隐式函数 通用 ,特别是噪声大、不均匀的点云
鲁棒、平滑、水密性好 可能平滑细节,计算量大
泊松表面重建 贪婪算法 需要保留细节、点云质量好
速度快,保留细节
局部算法,不保证水密
贪婪投影三角化
实际工作流建议:
- 预处理
:对原始点云进行去噪(例如,统计学滤波器)和下采样(例如,体素下采样),以减少计算量并提高鲁一性。
- 法线估计
:如果所选方法需要法向量(如泊松重建),则必须进行这一步。确保法线方向一致性至关重要。
- 重建
:对于大多数无序点云,首选泊松表面重建。如果它过于平滑,可以尝试贪婪投影或Alpha Shapes。如果数据是有序的高度图,直接用2.5D Delaunay。
- 后处理
:重建出的网格可能需要进一步处理,如平滑、孔洞填充、简化(减少面数)或细分(增加面数)。
PCL (Point Cloud Library) 和 Open3D 等开源库都提供了上述大部分算法的实现,是进行点云重建的强大工具。
11. 八叉树地图
我们来详细探讨一种在机器人学和3D计算机视觉中极其重要的地图表示方法——八叉树地图 (OctoMap)。
1. 核心思想:空间的分层与递归
想象一下,你要描述一个三维空间中哪些地方被占用了,哪些地方是空闲的。
最笨的方法:将整个空间划分成一个巨大的、固定大小的体素网格 (Voxel Grid)。然后为每个小方块(体素)标记“占用”、“空闲”或“未知”。
- 问题
:如果空间很大,或者你需要的精度很高(体素很小),这个网格将占用天文数字般的内存。例如,一个 100m x 100m x 20m 的空间,如果用 1cm 的分辨率,需要
10000 * 10000 * 2000 = 2000亿个体素,这在计算上是不可行的。
- 问题
八叉树的巧妙解决:八叉树采用了一种“分而治之”的递归思想。
如果整个立方体完全是空闲的,就直接将其标记为“空闲”,不再细分。
如果整个立方体完全是被占用的,就直接将其标记为“占用”,不再细分。
如果这个立方体内部既有空闲区域,也有占用区域(混合状态),就将其均匀地切分成八个等大的子立方体(就像切豆腐块一样)。这八个子立方体就成为当前节点的八个子节点。
从一个代表整个空间的巨大立方体(根节点)开始。
检查这个大立方体内部的状态:
对每一个子节点,递归地重复第2步的操作。
这个过程一直持续下去,直到达到预设的最小分辨率(最小的体素尺寸)。
结果:
在大片的同质区域(如空旷的房间中央或实心墙壁内部),八叉树用很少的几个大节点就能表示,极大地节省了内存。
只在物体表面附近的复杂区域,八叉树才会分裂到最精细的层级,以高分辨率来描述细节。
2. 八叉树的概率表示
仅仅标记“占用/空闲”是不够的,因为传感器的测量总是有噪声和不确定性的。OctoMap通过一种概率的方式来建模每个节点的状态。
每个节点(无论是叶子节点还是非叶子节点)都存储一个对数优势比 (Log-Odds) 的值来表示其被占用的概率。
log_odds = log( p / (1 - p) )其中
p是该节点被占用的概率。
为什么用对数优势比?
- 高效的贝叶斯更新
:当有新的传感器测量(例如,一束激光击中了某个点,或者没有击中)时,更新概率只需要进行加法或减法操作,这比乘法要快得多。
log_odds_new = log_odds_old + log_odds_measurement - 数值稳定性
:概率
p的取值范围是[0, 1],在接近0或1时更新会很慢。而对数优势比的范围是(-∞, +∞),没有这个问题。 - 表示未知状态
:一个新节点的初始
log_odds可以设为0,这对应于p=0.5,即“完全未知”。
- 高效的贝叶斯更新
节点状态判断:
当一个节点的
log_odds大于一个占用阈值,它被认为是被占用的。当
log_odds小于一个空闲阈值,它被认为是空闲的。介于两者之间则认为是未知的。
3. OctoMap的构建与更新流程
- 输入
:一系列来自传感器的3D点云(如LiDAR扫描或RGB-D深度图)以及对应的传感器原点位置。
- 射线投射 (Ray Casting)
:对于点云中的每一个测量点
P_end:
从传感器原点
P_origin到P_end之间画一条虚拟的射线。
- 预处理
- 更新节点
:
这条射线路径上穿过的所有体素,它们的被占用概率应该降低(因为光线能穿过,说明这里是空闲的)。这对应于将它们的
log_odds值减去一个表示“空闲”的对数值。射线终点所在的那个体素
P_end,它的被占用概率应该增加(因为光线在这里被挡住了)。这对应于将它的log_odds值加上一个表示“占用”的对数值。
- 树结构维护
:
在更新叶子节点的同时,其所有父节点的概率也会被相应更新(通常是其所有子节点概率的某种聚合,如最大值)。
如果一个父节点的所有子节点都变成了同一种状态(全占用或全空闲),这些子节点就可以被剪枝 (Pruning),由父节点统一表示,从而节省内存。
4. 八叉树地图的优缺点
优点
- 内存效率极高
:这是它最大的优点。相比于固定体素网格,它能以几个数量级的优势节省内存,使得在大规模场景下构建高分辨率地图成为可能。
- 分层数据结构
:可以根据需要在不同分辨率下查询地图。例如,进行粗略的全局路径规划时,可以使用较粗的层级;进行精细的避障时,可以使用最精细的层级。
- 高效更新
:概率更新机制非常高效。
- 同时表示已知和未知空间
:这对于机器人探索和路径规划至关重要。机器人倾向于探索“未知”区域。
- 开源库成熟
:
octomap是一个广泛使用的、与ROS(机器人操作系统)紧密集成的C++库,非常成熟和稳定。
缺点
- 非刚性变换困难
:八叉树是建立在一个固定的世界坐标系下的。如果地图需要进行变形或非刚性对齐(例如在回环闭合后修正地图),操作会非常复杂和低效。相比之下,点云地图进行变换就容易得多。
- 不存储原始点信息
:它只存储了体素的占用概率,丢失了原始点云的精确位置、颜色、法向量等信息。这使得它不适合用于需要高保真表面的应用(如三维重建可视化)。
- 坐标系对齐
:地图的轴线是与世界坐标系对齐的。如果场景本身是倾斜的,可能会导致不必要的细分,产生“锯齿”效应。
5. 主要应用
- 机器人路径规划与导航
:这是OctoMap最核心的应用。机器人可以利用地图规划出一条既能避开“占用”区域,又能穿过“空闲”区域的路径。
- 自主探索 (Autonomous Exploration)
:机器人可以利用地图中的“未知”区域信息,规划探索路径以最高效地建图。
- 碰撞检测
:快速检查一个机器臂或整个机器人的规划轨迹是否会与环境中的障碍物发生碰撞。
- 场景理解
:提供环境的基本三维结构。
总结
八叉树地图 (OctoMap) 是一种用于表示三维环境占用状态的、内存高效、支持概率更新、并具有多分辨率特性的数据结构。它牺牲了表面的几何精度,以换取在机器人导航和规划任务中至关重要的空间占用信息。可以说,如果你的任务是“能不能走”而不是“长什么样”,那么OctoMap就是不二之选。
12. TSDF地图和Fusion系列
我们来深入探讨一个在实时三维重建领域具有里程碑意义的技术系列——TSDF地图以及由其驱动的Fusion系列算法。
这个系列开启了消费级设备进行高质量、实时稠密建图的时代。
1. TSDF地图:一种优雅的表面表示法
我们在之前的讨论中已经多次提到 TSDF (Truncated Signed Distance Function),现在我们来系统地总结一下。
核心思想:不用点云来表示表面,而是用一个隐式函数来定义表面。这个函数定义在三维空间的一个体素网格 (Voxel Grid) 上。
SDF (Signed Distance Function):对于空间中的任意一点(体素中心),SDF的值是该点到最近物体表面的有符号距离。
- 符号
:在物体外部为正,内部为负。
- 数值
:到表面的最短欧氏距离。
- 关键特性
:物体表面本身就是SDF=0的等值面 (Isosurface)。
- 符号
T (Truncated):这是为了效率和内存进行的优化。我们只关心物体表面附近区域的精确距离。对于离表面很远的体素,我们不需要存储精确的距离值,直接将其“截断”为一个固定的最大值(如
+1)或最小值(如-1)。这个精确计算的区域被称为截断带 (Truncation Band)。融合 (Fusion):TSDF的强大之处在于它的融合能力。每个体素不仅存储SDF值,还存储一个权重 (Weight),表示该SDF值估计的置信度。当一个新的深度图到来时,可以通过加权平均的方式,不断地将新的测量值融合到已有的TSDF网格中。
SDF_new = (W_old * SDF_old + W_curr * SDF_curr) / (W_old + W_curr)W_new = W_old + W_curr
这个过程能够有效地平滑掉单次测量的噪声,得到一个非常平滑和精确的表面模型。
总结TSDF的优点:
- 隐式表示
:避免了处理离散点云的复杂性。
- 噪声鲁棒性
:加权平均的融合机制能有效抑制传感器噪声。
- 水密性
:天生倾向于生成封闭、无孔洞的表面。
- 高效提取
:可以非常高效地通过移动立方体 (Marching Cubes) 算法提取出三角网格,或通过光线投射 (Ray Casting) 进行实时渲染。
2. Fusion系列算法:将TSDF推向巅峰
Fusion系列算法的核心就是将TSDF体素融合与实时的相机跟踪相结合,形成一个完整的、端到端的实时三维重建系统。
a) KinectFusion (2011年,微软研究院)
这是整个系列的开山之作,也是一个时代的标志。它首次展示了仅用一个消费级的Kinect相机和一个GPU,就能实现惊人的实时3D扫描效果。
核心流程:
- 相机跟踪 (Tracking)
:使用ICP (Iterative Closest Point) 算法。将当前帧的深度图转换成的点云,与上一帧从全局模型中渲染出的虚拟点云进行配准,从而计算出当前相机的位姿。
- 数据融合 (Mapping/Fusion)
:利用计算出的新位姿,将当前帧的深度数据融合到全局的TSDF体素网格中。
- 表面渲染 (Rendering)
:使用光线投射 (Ray Casting) 从更新后的TSDF模型中,根据当前相机位姿渲染出一幅虚拟的深度图和表面图。这幅图不仅用于可视化,更重要的是作为下一帧ICP跟踪的目标。
局限性:
- 内存限制
:它使用一个固定大小的体素网格来表示整个场景。这意味着场景大小和分辨率都受到GPU显存的严格限制(通常只能扫描桌面大小的物体)。
- 无回环检测
:纯粹的帧到模型跟踪会产生累积误差,无法处理回环和大规模场景。
b) Kintinuous (2012年,帝国理工学院)
Kintinuous是对KinectFusion的直接扩展,旨在解决其场景规模的限制。
- 核心改进:地图滚动/移位 (Map Shifting)
TSDF体素网格不再是固定在世界坐标系中的,而是以相机为中心。
当相机移动到接近TSDF网格的边界时,整个网格在内存中进行一次“移位”操作。
从视野中移出的那部分TSDF数据,会被提取成三角网格面片 (Mesh Slices),并存储起来。
这样,GPU内存中始终只维护相机周围的一小块活动区域,理论上可以重建任意规模的场景。
它还引入了基于RGB特征的回环检测和位姿图优化,以处理累积误差。
c) ElasticFusion (2015年,帝国理工学院)
这是另一个革命性的工作,它解决了KinectFusion和Kintinuous都无法处理的动态回环闭合问题。
核心改进:基于形变图的非刚性地图修正 (Deformation Graph for Non-rigid Map Correction)
地图不再是单一的刚性模型,而是由许多小的面元 (Surfel) 组成,这些面元通过一个形变图 (Deformation Graph) 连接在一起。
当检测到回环时,系统不会像传统SLAM那样对相机轨迹进行刚性修正,而是会**“弹性地”弯曲和扭转**整个地图,使得回环处的两端能够完美地对齐,同时将这种形变平滑地传递到整个地图的其他部分。
这使得它在处理累积误差和闭合回环时,效果非常出色,不会出现地图断裂或重影。
与TSDF的区别:ElasticFusion没有使用TSDF体素网格,而是直接使用面元 (Surfel) 作为地图的基本表示。但其思想(融合和优化)与Fusion系列一脉相承。
d) InfiniTAM (2015年,牛津大学)
InfiniTAM从另一个角度解决了KinectFusion的内存问题,并且设计成了一个高度模块化和可扩展的框架。
- 核心改进:哈希体素 (Voxel Hashing)
这是由Niessner等人提出的天才想法。它不再需要为一个巨大的、连续的体素网格预先分配内存。
它将空间划分为固定大小的体素块 (Voxel Blocks)(例如8x8x8的体素)。
使用一个哈希表 (Hash Table) 来管理这些体素块。只有当一条射线穿过某个空间区域时,系统才会在哈希表中为该区域对应的体素块动态分配内存。
- 效果
:内存使用量只与实际物体表面的面积成正比,而与整个场景的体积无关。这使得在有限的内存下重建大规模场景成为可能,且无需像Kintinuous那样进行复杂的地图移位操作。
- 框架化
:InfiniTAM被设计成一个框架,方便研究者扩展和替换其中的模块,例如跟踪方法、融合策略等。
总结与对比
算法
核心思想
解决了什么问题
地图表示
KinectFusion ICP跟踪 + TSDF融合
实现了实时的稠密重建
全局固定TSDF体素网格
Kintinuous 地图滚动与切片
场景规模限制 移动的TSDF体素网格 + 网格面片
ElasticFusion 形变图非刚性修正
动态回环闭合 面元 (Surfels) + 形变图
InfiniTAM 哈希体素
内存限制 (另一种方式)
基于哈希的稀疏TSDF体素块
TSDF 作为一种数据结构,是这个技术浪潮的基石。而 Fusion系列算法 则是在这个基石上,不断地通过创新的系统设计(如地图滚动、形变图、哈希)来解决实时三维重建在规模、内存、精度和鲁棒性方面遇到的核心挑战,共同推动了整个领域的发展。
二、代码笔记
1. dense_mapping.cpp
该程序实现了一个基于滤波思想的单目稠密深度估计方法。它以一帧图像作为参考帧,然后利用后续的视频帧和已知的相机位姿,逐步地、稠密地(即为每个像素)估计出参考帧的深度图。
程序的核心工作流程如下:
初始化:程序选择第一张图像作为参考帧,并为参考帧的所有像素初始化一个深度分布。这个分布用均值(一个初始猜测值,如3米)和方差(表示不确定性的大小)来描述。
迭代更新:程序遍历后续的每一帧图像(称为当前帧):
- 极线搜索 (
epipolarSearch):对于参考帧中的每一个像素,程序不是在当前帧的整个图像中搜索匹配,而是在一条称为极线的直线上进行搜索。这是因为该像素对应的空间点必然会投影到当前帧的这条极线上。此外,利用当前深度的不确定性(方差),可以将搜索范围进一步缩小到极线上的一个线段内。
- 块匹配 (
NCC):在极线段上进行采样,对于每个采样点,计算其周围的一个小图像块(patch)与参考帧中对应像素的图像块之间的**归一化互相关(NCC)**得分。NCC是一种对亮度变化不敏感的相似性度量。得分最高的采样点被认为是最佳匹配。
- 深度更新 (
updateDepthFilter):一旦找到了可靠的匹配点,就相当于有了一个新的观测。程序:
通过三角测量从这个新的匹配对中计算出一个新的深度值。
估计这个新深度值的不确定性。
使用高斯融合(或可视为一个简单的一维卡尔曼滤波器),将这个新的观测(深度和不确定性)与该像素已有的深度分布进行融合,得到一个更新后的、更精确的深度均值和更小的不确定性(方差)。
- 内存限制
收敛与评估:这个迭代过程不断重复。随着观测的增多,每个像素的深度估计会越来越准,其方差会越来越小。当方差小于一定阈值时,认为该点的深度已经收敛。程序在每一步都将估计的深度图与真实的深度图进行比较,以评估算法性能。


这份代码是一个非常经典的、基于极线搜索和NCC匹配的单目稠密建图实现,它很好地演示了核心原理。针对这份代码的“故意暴露的问题”,我们可以从效率、鲁棒性和精度三个方面提出一系列改进措施。
一、 效率提升 (Performance Improvements)
当前代码最显著的问题是效率。它在每一帧都对参考图像中所有未收敛的像素进行完整的极线搜索和更新,这是非常耗时的。
1. 引入关键帧机制 (Keyframe-based Approach)
- 问题
:当前代码使用第一帧作为唯一的参考帧 (
ref),所有后续帧都与它进行匹配。当后续帧与第一帧的视角差异过大时,匹配会变得非常困难且不可靠。同时,与每一帧都进行比较是冗余的。 - 改进
:
不再固定第一帧为参考帧。选择一系列视差和角度都足够大的关键帧 (Keyframes)。
只在新的关键帧被创建时,才对像素的深度进行更新。
对于一个像素的深度估计,可以利用多个关键帧的信息,而不仅仅是两帧。
- 问题
- 代码修改
:
在
main函数的循环中,增加一个判断逻辑:if (isNewKeyframe(pose_curr_TWC, last_keyframe_pose))。这个函数可以基于平移和旋转的大小来判断。如果不是关键帧,直接跳过
update。如果是关键帧,则将
curr图像和位姿作为新的观测帧,对参考帧的深度图进行更新。可以考虑将最近的几个关键帧都用来更新深度,以提高鲁棒性。
2. 并行化处理 (Parallelization)
- 问题
:
update函数中的双层for循环是串行的,而每个像素的深度估计过程是相互独立的。 - 改进
:使用多线程(如 C++11
std::thread或 OpenMP)来并行化处理这个双层循环。 可以将图像分成 N 个水平条带 (stripes),每个线程负责处理一个条带的像素。
- 代码修改
:
注意:要确保并行代码中没有数据竞争。在这里,// in update function // #include <omp.h> #pragmaomp parallel for for(int y = boarder; y < height - boarder; y++){ for(int x = boarder; x < width - boarder; x++){ // ... a single pixel's update logic ... } }depth和depth_cov2的每个像素只被一个线程写入,所以是线程安全的。
3. 优化NCC计算 (Optimize NCC Calculation)
- 问题
:
NCC函数中,每次都重新创建vector并计算窗口均值,效率较低。 - 改进
:使用积分图 (Integral Image) 技术可以极大地加速窗口内像素值求和的过程。
对参考图像和当前图像预先计算积分图。
之后,任何矩形窗口内的像素和都可以通过4次数值查找和加减法在 O(1) 时间内完成。
- 代码修改
:
在
update函数开始前,为ref和curr计算积分图和平方积分图。修改
NCC函数,利用积分图来快速计算mean_ref,mean_curr,demoniator1,demoniator2。这会将NCC的计算复杂度从 O(N*N) 降低到 O(1)(N是窗口大小)。
二、 鲁棒性增强 (Robustness Enhancements)
1. 引入逆深度参数化 (Inverse Depth Parametrization)
- 问题
:代码直接对深度
depth进行滤波。这对于远处点和初始化阶段非常不利,因为深度的不确定性不是高斯的。 - 改进
:
不要存储和更新
depth和depth_cov2,而是存储和更新逆深度inv_depth = 1.0 / depth和其方差inv_depth_cov2。初始化时,可以将
inv_depth初始化为 0,表示无穷远,这比初始化一个武断的3.0米要合理得多。方差可以初始化为一个较大的值。所有的滤波、更新、三角化计算都应该在逆深度空间进行。
- 代码修改
:
Mat depth->
Mat inv_depth。epipolarSearch中的搜索范围
d_min, d_max需要从逆深度的均值和方差转换而来。updateDepthFilter中的高斯融合应在逆深度上进行。
2. 采用均匀-高斯混合分布滤波器 (Uniform-Gaussian Mixture Filter)
- 问题
:当前的高斯滤波器在面对错误的初始匹配时非常脆弱,可能会收敛到错误值。
- 改进
:为每个像素的深度维护一个更复杂的模型:
p(d) = π * U(d_min, d_max) + (1 - π) * N(μ, σ²)。 - 代码修改
:
depth_cov2矩阵需要被替换,或者增加一个
Mat depth_pi(height, width, CV_64F)来存储混合权重。updateDepthFilter函数需要被重写,以实现均匀-高斯混合模型的更新逻辑。这会使代码更复杂,但鲁棒性会大幅提升,尤其是在低纹理区域。
3. 左右一致性检查 (Left-Right Consistency Check)
- 问题
:当前的匹配是单向的(从参考帧到当前帧)。如果当前帧的一个区域是无纹理的,可能会错误地匹配到参考帧的某个有纹理的区域。
- 改进
:增加一个反向匹配验证。
在
epipolarSearch找到最佳匹配点pt_curr后,再从pt_curr出发,在参考帧ref中沿着极线反向搜索,看是否能匹配回原始点pt_ref附近。只有当
||pt_ref_reprojected - pt_ref||小于一个阈值(如1-2个像素)时,才认为这次匹配是有效的。
- 代码修改
:
在
epipolarSearch的末尾,在return true之前,增加一个反向搜索的逻辑。这会增加计算量,但能有效剔除大量由遮挡或无纹理引起的误匹配。
三、 精度提升 (Accuracy Improvements)
1. 亚像素级精度的极线搜索 (Sub-pixel Refinement)
- 问题
:
epipolarSearch中的循环步长是固定的0.7。这导致最终找到的最佳匹配点best_px_curr是离散的,其精度受限于步长。 - 改进
:在找到离散的最佳匹配点后,进行一次亚像素级别的优化。
对离散最佳点及其左右两个邻居的NCC值进行二次函数拟合。
二次函数的顶点对应的位置就是亚像素精度的最佳匹配位置。
- 代码修改
:
在
epipolarSearch的for循环结束后,不要直接返回best_px_curr。取
best_ncc及其左右两个点的NCC值,拟合抛物线y = ax^2 + bx + c,解出顶点-b/2a,得到亚像素级别的偏移量,从而更新pt_curr。
2. 考虑相机运动的不确定性 (Propagate Pose Uncertainty)
- 问题
:代码假设位姿
T_C_R是完全精确的,这在实际SLAM系统中是不可能的。位姿的不确定性会影响极线的位置和三角化的精度。 - 改进
:在计算深度不确定性
d_cov2时,不仅要考虑一个像素的匹配误差,还应该通过协方差传播,将位姿T_C_R的不确定性也考虑进去。 - 代码修改
:
这是一个非常高级的改进。需要修改
updateDepthFilter函数。函数的输入需要增加位姿的协方差矩阵。在计算
d_cov2时,需要用到雅可比矩阵,将位姿的不确定性传播到三角化后的深度不确定性上。这会使数学推导变得复杂。
总结与建议的修改顺序
对于这份代码,一个实际的改进路径可以是:
【高优先级 - 效果显著】:
- 并行化
:最容易实现,能立刻看到性能提升。
- 引入关键帧
:能解决核心的效率和鲁棒性问题。
- 改用逆深度
:对算法的稳定性和理论完备性有巨大提升。
【中优先级 - 提升鲁棒性】:
- 左右一致性检查
:能显著减少误匹配,让深度图更干净。
- 亚像素插值
:提升匹配精度,对最终的深度图质量有帮助。
- 左右一致性检查
【低优先级 - 高级/复杂】:
- 优化NCC计算(积分图)
:如果并行化后性能仍是瓶颈,可以考虑。
- 均匀-高斯混合分布
:重构滤波器,代码改动大,但能解决根本性的鲁棒问题。
- 传播位姿不确定性
:理论上最完备,但实现复杂,需要对状态估计算法有深入理解。
通过这些改进,这份教学性质的代码可以一步步地被改造成一个更接近于研究和工业界水准的、高效且鲁棒的稠密建图系统。
2. octomap_mapping.cpp RGB‑D 构建 OctoMap



3. pointcloud_mapping.cpp RGB‑D 构建稠密点云并滤波
该C++程序使用PCL (Point Cloud Library) 库来处理和构建三维点云。它与之前的OctoMap示例目标相似,都是从RGB-D数据和相机位姿重建三维场景,但它侧重于生成和处理几何点云,而不是构建占据栅格地图。
程序的主要工作流程如下:
数据加载与点云生成:
程序首先加载RGB-D图像序列和对应的相机位姿,这与之前的示例相同。
它遍历每一帧数据,通过反投影和坐标变换,将每个有效的深度像素转换为世界坐标系下的一个带颜色的三维点 (XYZRGB)。
这些点被组织成PCL的
pcl::PointCloud<pcl::PointXYZRGB>数据结构。
- 优化NCC计算(积分图)
点云滤波:这是本程序的核心亮点,展示了PCL强大的点云处理能力。
- 统计离群点移除 (Statistical Outlier Removal)
:对于每一帧生成的点云,程序首先使用统计滤波器来移除噪声点(离群点)。该滤波器计算每个点到其邻域点的平均距离,并剔除那些距离远大于平均距离标准差的孤立点。这有助于提高单帧点云的质量。
- 体素栅格滤波 (Voxel Grid Filter)
:在所有帧的点云(经过初步滤波后)被拼接成一个大的全局点云之后,程序使用体素滤波器对这个全局点云进行下采样 (Downsampling)。该滤波器将三维空间划分为一个个小的立方体(体素),并用每个体素内所有点的质心来代表该体素,从而在保持点云整体形状的同时,减少点的数量,使得点云更均匀、更易于处理和存储。
- 统计离群点移除 (Statistical Outlier Removal)
点云拼接与保存:
经过离群点移除的单帧点云被累加到一个全局的
pointCloud对象中。在所有帧处理完毕后,这个大的、拼接好的点云再经过体素滤波进行下采样。
最后,程序将处理完成的、干净且大小适中的全局点云保存为一个标准的
.pcd文件,这个文件可以被PCL的其他工具或CloudCompare等三维软件加载和可视化。


4. surfel_mapping.cpp 点云曲面重建
该C++程序使用PCL (Point Cloud Library) 库,演示了从一个无组织的三维点云重建出三角网格(Mesh)表面的完整流程。这是三维重建领域一个非常重要的步骤,它将离散的点云数据转换为具有拓扑连接的连续表面模型。
程序的主要工作流程如下:
加载点云:程序首先从一个
.pcd文件加载输入的原始点云数据。表面平滑与法线估计 (
reconstructSurface):
在进行网格化之前,通常需要对原始点云进行预处理,因为真实的扫描数据往往带有噪声和不均匀的密度。
程序使用了移动最小二乘法 (Moving Least Squares, MLS)。MLS是一种强大的点云平滑技术,它通过在每个点的局部邻域内拟合一个多项式曲面,然后将该点投影到这个拟合的曲面上,从而达到平滑效果。
在平滑的同时,MLS还能够非常准确地估计出每个点的法线向量(Normal Vector)。法线信息对于后续的表面重建至关重要,因为它描述了每个点所在局部表面的朝向。
这一步的输出是一个新的点云,其中每个点不仅有坐标和颜色,还包含了计算出的法线信息(即
SurfelCloud)。
网格化 (
triangulateMesh):这是程序的核心步骤,它将带有法线的平滑点云转换为一个三角网格。
程序使用了贪心投影三角化 (Greedy Projection Triangulation) 算法。这是一种快速且直观的网格化方法。
- 核心思想
:算法从一个点开始,将其投影到一个由其法线定义的局部平面上。然后,它在该平面上搜索该点的邻居,并将最近的、满足一定几何约束(如距离、角度)的邻居点连接起来形成三角形。这个过程像滚雪球一样不断扩展,直到所有点都被连接成一个流形网格。
通过设置各种参数(如最大边长、最小/最大角度、法线一致性等),可以控制生成网格的质量。
可视化:
最后,程序使用PCL的
PCLVisualizer来可视化最终生成的三角网格。它同时显示了网格的填充面和线框,让用户可以清晰地观察重建出的三维模型表面。






















 2051
2051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








