【MR】现代机器人学-第六章-逆运动学

一、本章小结

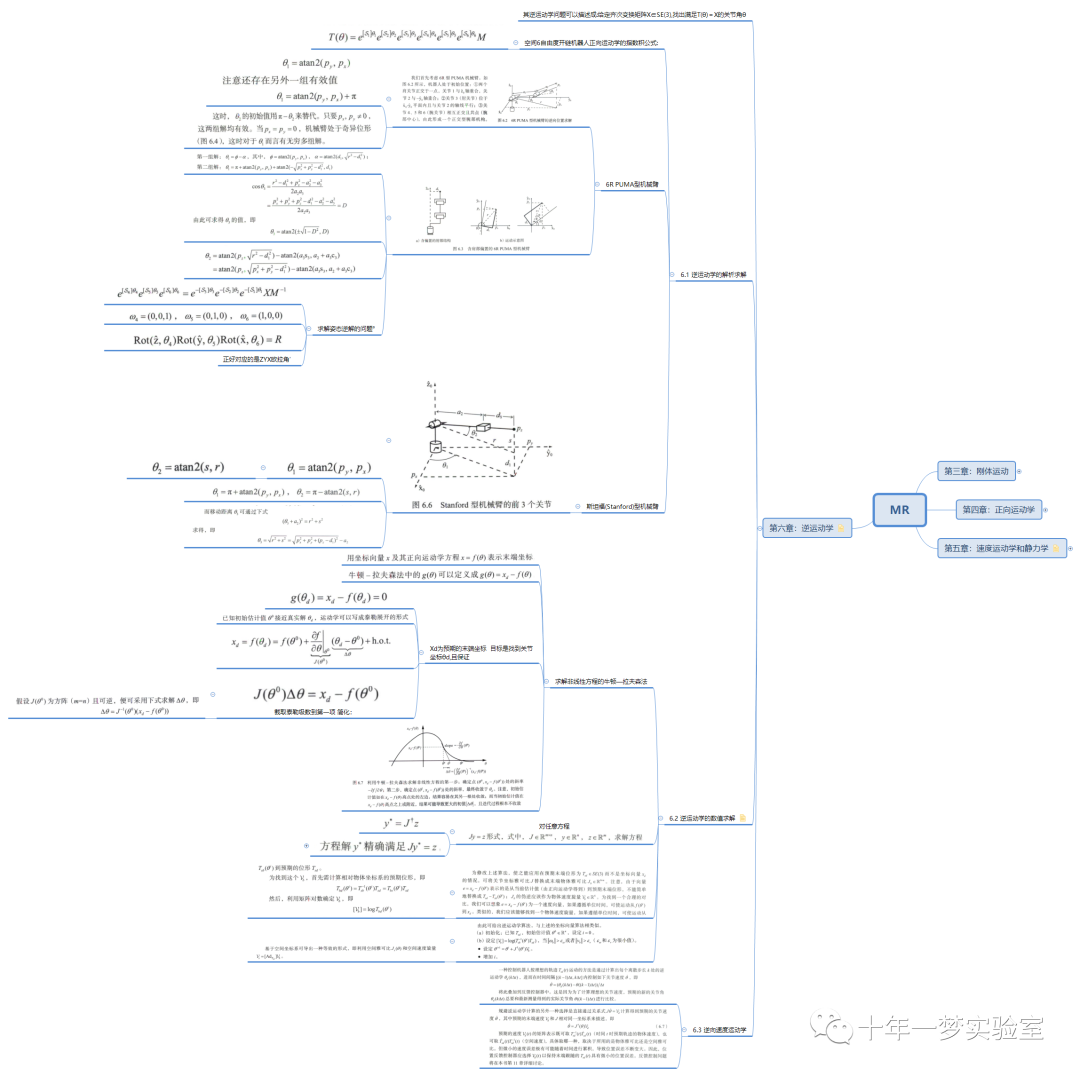
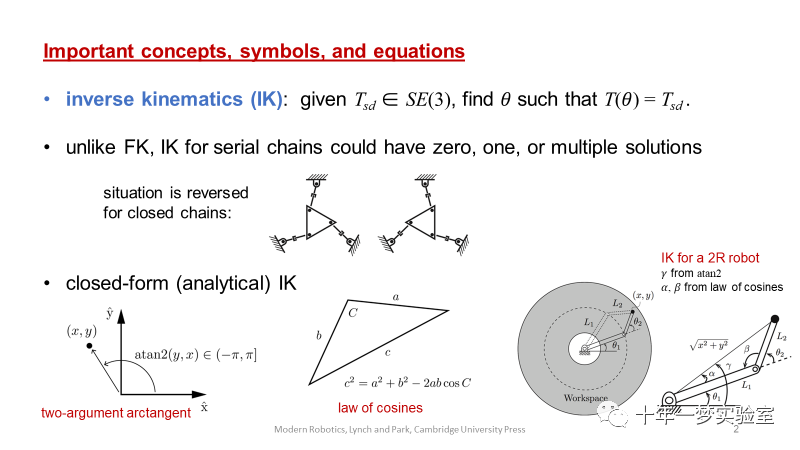
给定一个具有正向运动学 T(θ), θ ∈ Rn 的空间开链，在逆运动学问题中，人们试图找到，对于所需的末端执行器配置 X ∈ SE(3)，满足 X = T(θ) 的解 θ . 与正运动学问题不同，逆运动学问题可以有多个解，或者在 X 位于工作空间之外的情况下没有解。对于具有 n 个关节且 X 在工作空间中的空间开链机器人，n = 6 通常会导致有限数量的逆运动学解决方案，而 n > 6 会导致无限数量的解决方案。

六自由度 PUMA 型机器人手臂的逆运动学可以解析求解，这是一种流行的 6R 设计，相互正交的3R腕部与相互正交的2R肩部通过肘部相连。

Stanford型机械臂的逆运动学也具有解析解 ,与PUMA型机械臂不同的是 该机 器人的肘部关节为P副而非R副。相应的逆运动学几何求解算法也开发出来,与 PUMA型机械臂的类似。

在逆运动学计算过程中无法得到解析解的情况下可以采用数值迭代方法。这些方 法通常会涉及像牛顿-拉夫森方法那样的迭代过程来求解逆运动学方程,并且通 常需要对关节变量赋初值,迭代过程的效果很大程度上取决于初值选取的质量 上,并且在存在多组运动学逆解的情况下,该方法能找到最接近初值的解。每次 迭代满足如下形式:

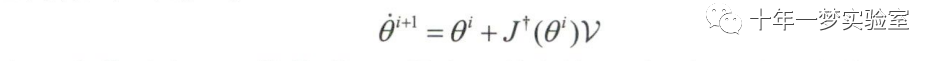
二、软件

[thetalist,success] = IKinBody(Blist,M,T,thetalist0,eomg,ev)

[thetalist,success] = IKinSpace(Slist,M,T,thetalist0,eomg,ev)

三、PPT

The End