【MR】现代机器人学-第五章-速度运动学和静力学

一、 本章小结

• Let the forward kinematics of an n-link open chain be expressed in the following product of exponentials form:

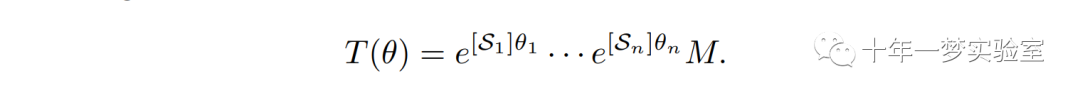
• Let the forward kinematics of an n-link open chain be expressed in the following product of exponentials form:

The body and space Jacobians are related via

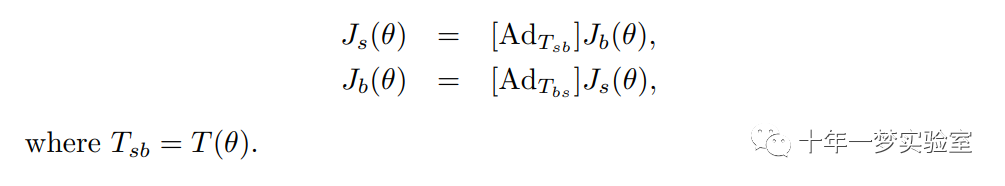
• 考虑具有 n 个单自由度关节的空间开链，假设处于静态平衡状态

Consider a spatial open chain with n one-dof joints that is assumed to be in static equilibrium（静态平衡）. Let τ ∈ R n denote the vector of the joint torques and forces and F ∈ R 6 be the wrench applied at the end-effector, in either space- or body-frame coordinates. Then τ and F are related by

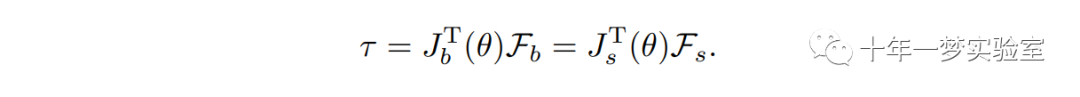
• 运动学奇异是指当雅可比矩阵不满秩情况下的任一位形θ：

A kinematically singular configuration for an open chain, or more simply a kinematic singularity, is any configuration θ ∈ R（n） at which the rank of the Jacobian is not maximal. For six-dof spatial open chains consisting of revolute and prismatic joints, some common singularities include (i) two collinear revolute joint axes; (ii) three coplanar and parallel revolute joint axes; (iii) four revolute joint axes intersecting at a common point; (iv) four coplanar revolute joints; and (v) six revolute joints intersecting a common line.

• 可操作性椭球描述了机器人在不同方向上移动的难易程度。

•  力椭球描述了机器人在不同方向上产生力的难易程度。

• 可操作度椭球与力椭球的度量指标包括

Measures of the manipulability and force ellipsoids include the ratio of the longest principal semi-axis to the shortest（长半轴与短半轴比值）; the square of this measure; and the volume of the ellipsoid. The first two measures indicate that the robot is far from being singular if they are small (close to 1).

二、软件

Jb = JacobianBody(Blist,thetalist)

Js = JacobianSpace(Slist,thetalist)

The End