【MR】现代机器人学-第九章-轨迹生成

本章基于Time Scaling（时间标度）进行轨迹生成的应用，在ROS中对应MoveIt官方文档的 Time Parameterization 这一教程。

https://ros-planning.github.io/moveit_tutorials/doc/time_parameterization/time_parameterization_tutorial.html 

MoveIt 可以支持不同的算法来对运动轨迹进行后处理，以添加时间戳和速度/加速度值。目前在 MoveIt 中默认提供三种：

• Iterative Parabolic Time Parameterization

• Iterative Spline Parameterization

• Time-optimal Trajectory Generation

一、本章小结

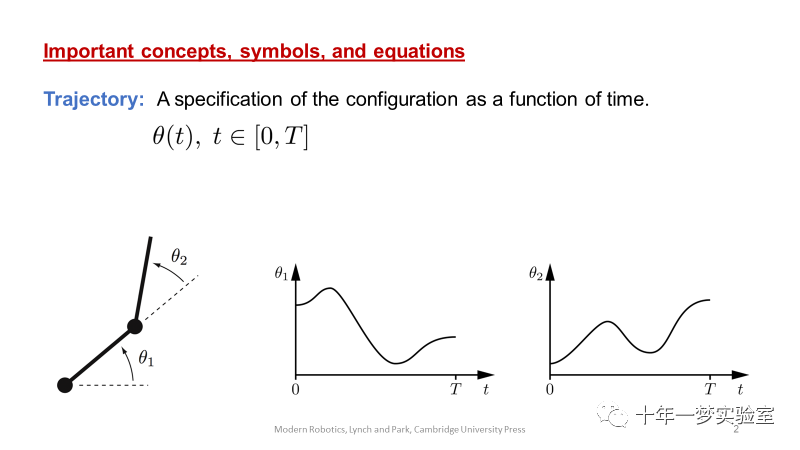
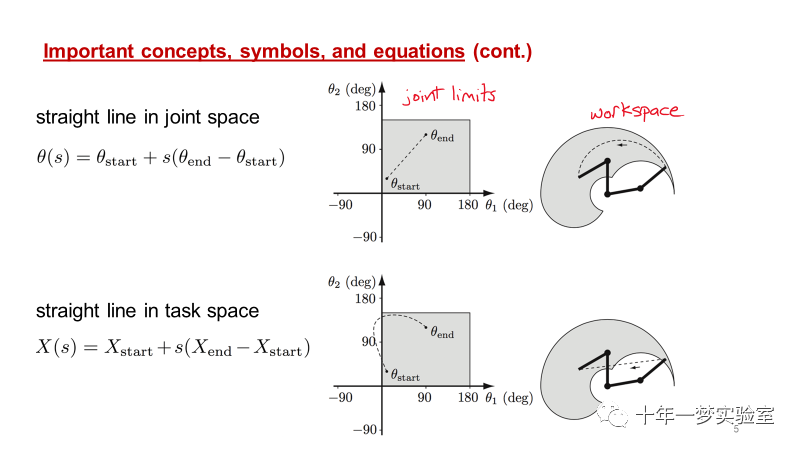
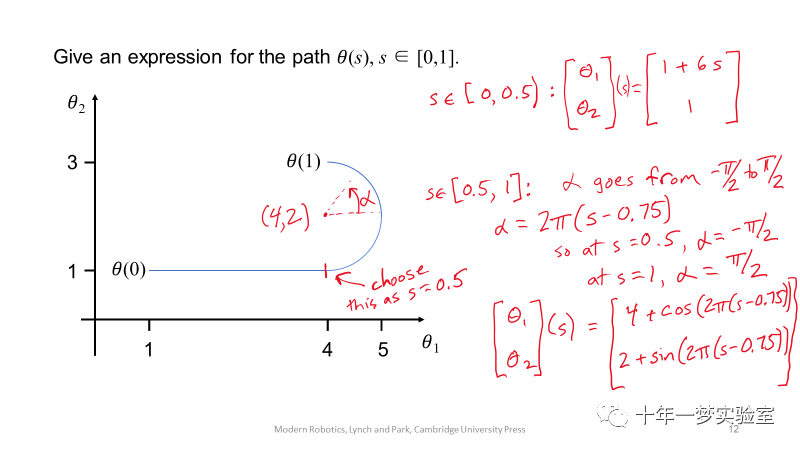
1. 轨迹θ(t)可表示为路径θ(s)和时间标度s(t)的组合形式。

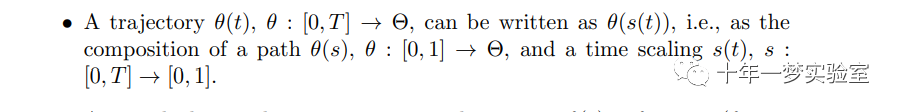
2. 关节空间的直线路径和任务空间的直线路径表示：

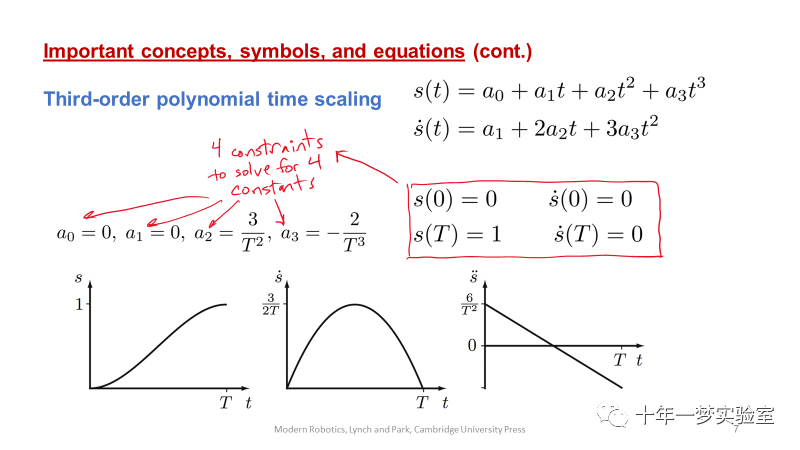
3. 三次多项式可用于对初始速度和最终速度均为零的点对点运动进行时间标度。在t=0和t=T时刻，加速度会经历阶跃变化（加加速度无限大），这种冲击脉冲会引起机器人的震动。

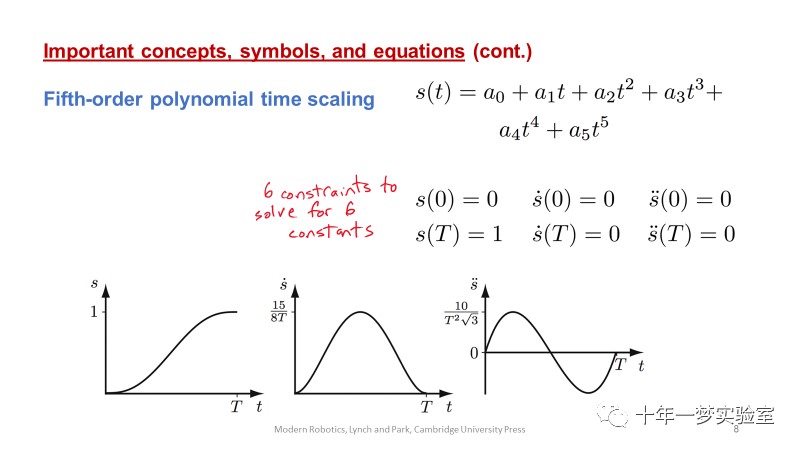
4. 五次多项式可用于对初始速度、最终速度、初始加速度和最终加速度全部为零的点对点运动进行时间标度，在任何时刻的加加速度都是有限值。

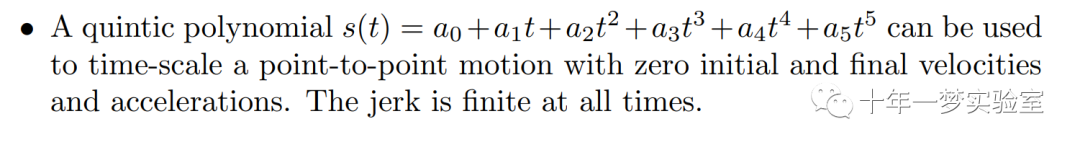
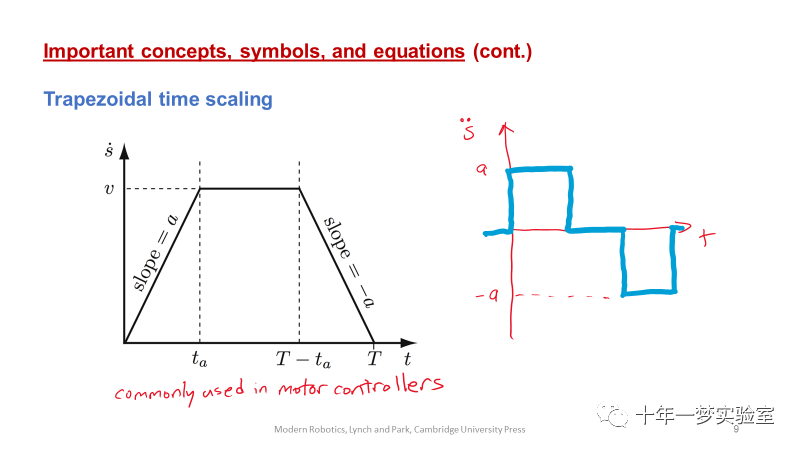
5. 梯形速度曲线是点对点控制中，尤其是单个点集控制中流行的一种时间标度。该运动由下列三个阶段组成：恒定加速度阶段、恒定速度阶段和恒定减速度阶段，这使得速度曲线为梯形。梯形运动中涉及加速度的阶跃变化。

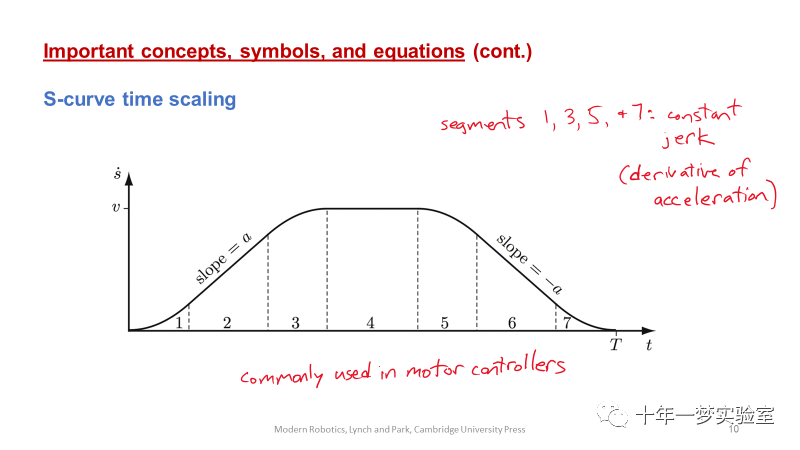
6. S-曲线运动在电机的点对点控制中也很流行。他有下列7个阶段组成：1-恒定正加加速度阶段；2-恒定加速度阶段；3-恒定负加加速度阶段；4-恒定速度阶段；5-恒定负加加速度阶段；6-恒定减速度阶段；7-恒定正加加速度阶段。

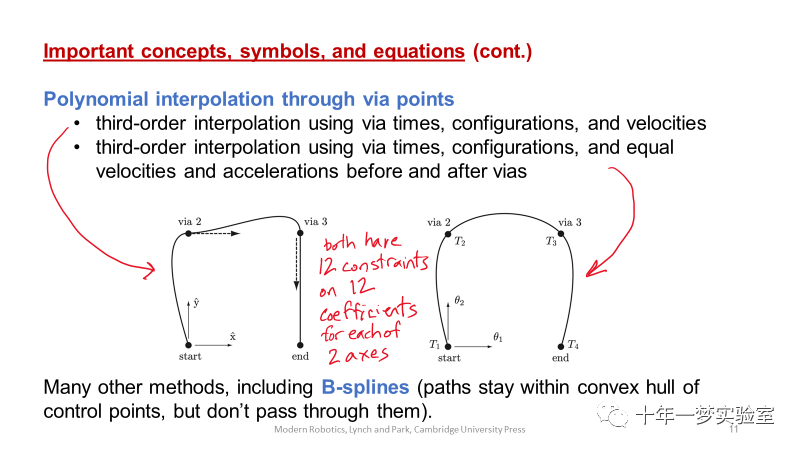
7. 给定一组中间点，包括开始状态、目标状态和机器人运动必须通过的其他中间状态，以及应该达到这些状态的时间Ti,一组三次多项式时间标度可用于生成对中间点做内插的轨迹θ(t).为了防止中间点处的加速度发生阶跃变化，可以使用一组五次多项式来代替。

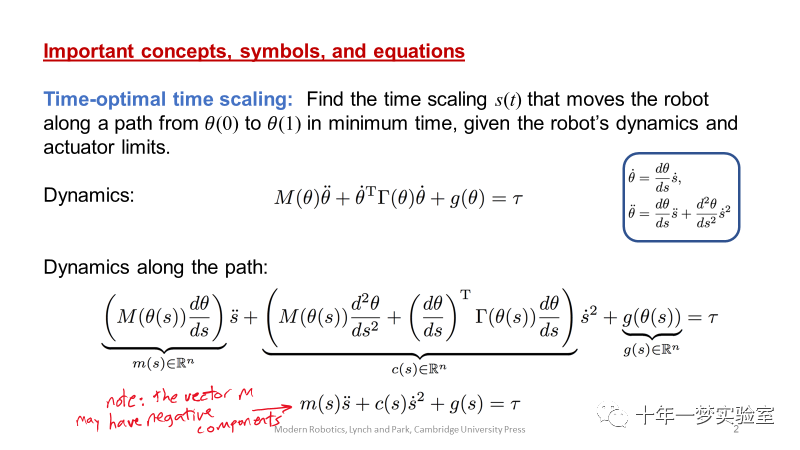
8.  给定机器人路径θ(s)，机器人的动力学，以及对执行器扭矩的限制，执行器约束可以表示为下列不等式形式：

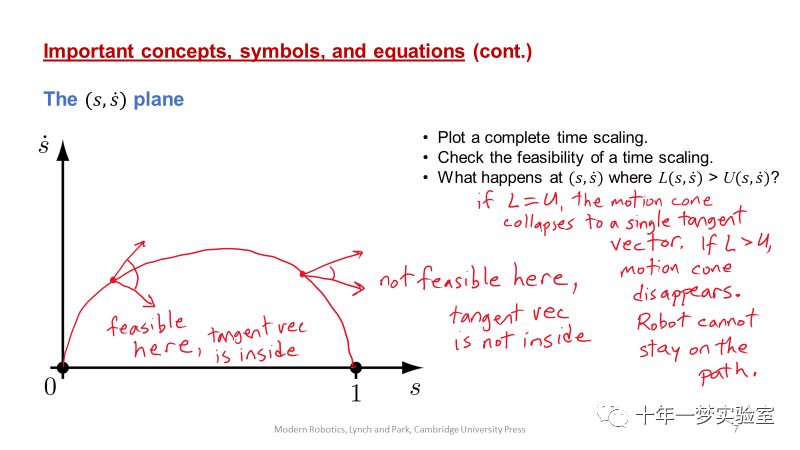
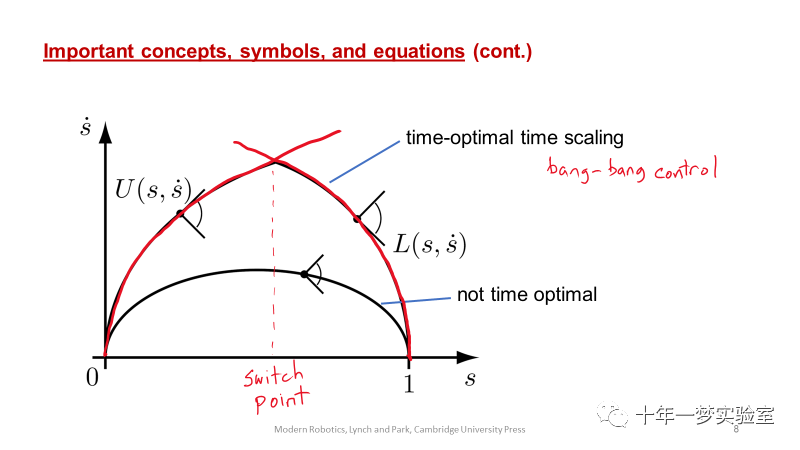
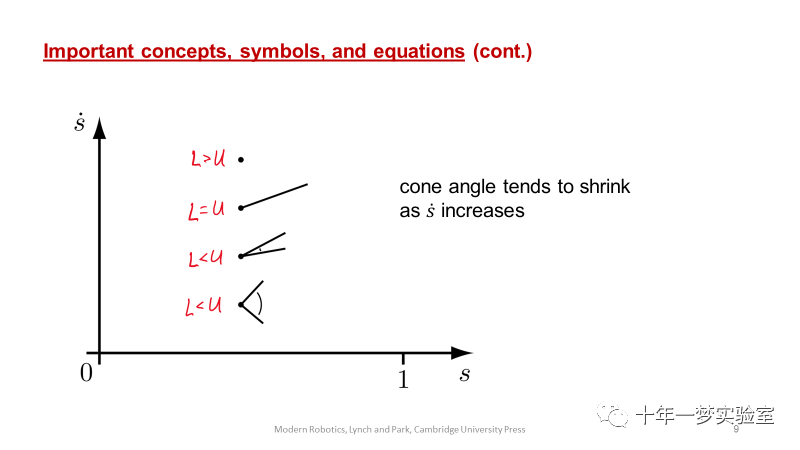
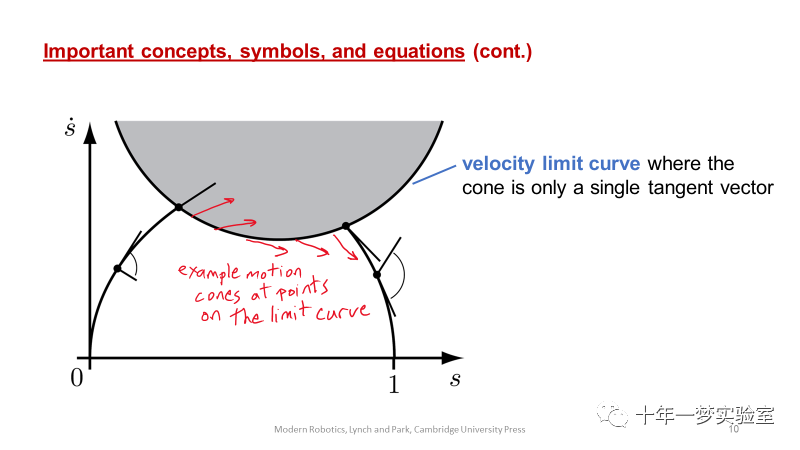
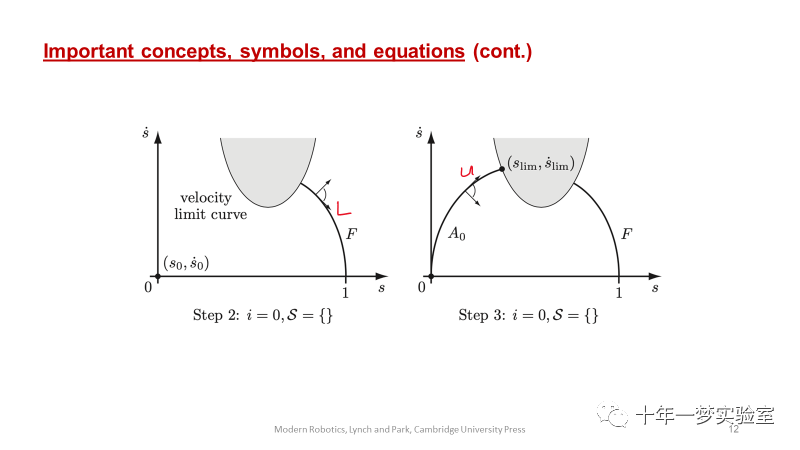
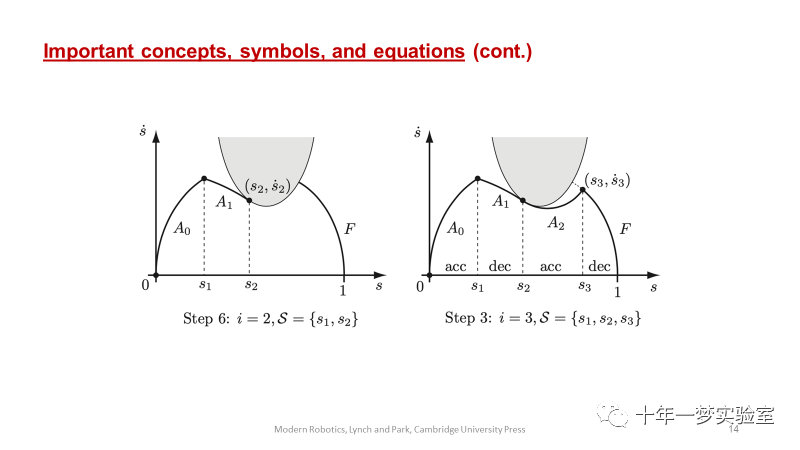
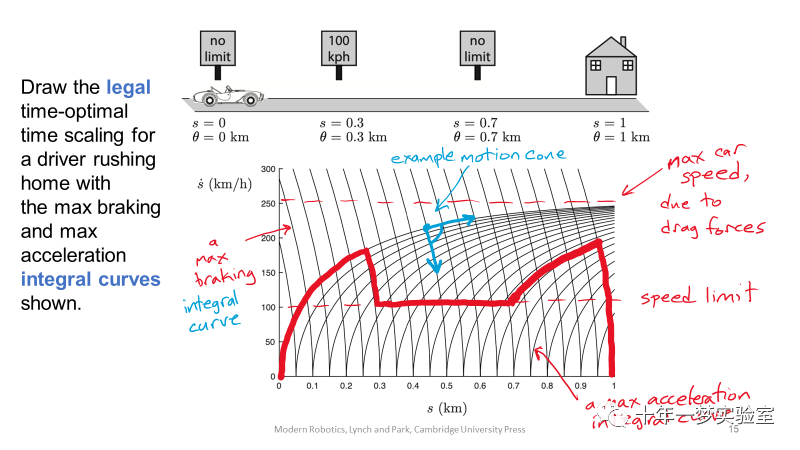
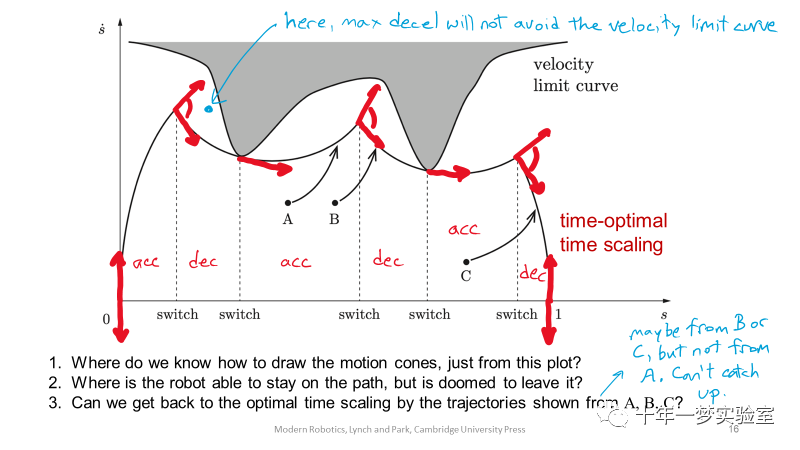
时间最优标度可以使(s, s˙) 相平面的曲线“高度”最大化，同时满足s(0) = ˙s(0) = ˙s(T) = 0, s(T) = 1以及执行器约束。最优解始终以最大加速度U(s, s˙)或者最大减速度L(s, s˙)运行。

二、软件

1.     s = CubicTimeScaling(Tf,t)

Computes s(t) for a cubic time scaling, given t and the total time of motion Tf .

2.     s = QuinticTimeScaling(Tf,t)

Computes s(t) for a quintic time scaling, given t and the total time of motion Tf .

3.     traj = JointTrajectory(thetastart,thetaend,Tf,N,method)

4.     traj = ScrewTrajectory(Xstart,Xend,Tf,N,method)

5.     traj = CartesianTrajectory(Xstart,Xend,Tf,N,method)

三、PPT

The End