自动控制原理 第三章（线性系统的时域分析与校正）【上】

一、概述

1、时域法的作用和特点

（1）时域法是最基本的分析方法，是学习复域法、频域法的基础。

（2）时域法的特点：

①直接在时间域中对系统进行分析校正，直观，准确。

②可以提供系统时间响应的全部信息。

③基于求解系统输出的解析解，比较烦琐。

2、时域法常用的典型输入信号

3、线性系统时域性能指标

（1）对控制系统的三个要求：

①稳：系统受扰动影响后能回到原来的平衡位置。（基本要求）

②准：稳态输出与理想输出间的误差（稳态误差）要小。（稳态要求）

③快：阶跃响应的过渡过程要平稳、迅速。（动态要求）

（2）动态性能：

①系统动态性能是以系统阶跃响应为基础来衡量的，一般认为阶跃输入对系统而言是比较严峻的工作状态，若系统在阶跃函数作用下的动态性能满足要求，那么系统在其它形式的输入作用下，其动态性能也应是令人满意的。

②动态性能指标通常有如下几项：

[1]延迟时间：阶跃响应第一次达到终值的50％所需的时间。

[2]上升时间：阶跃响应从终值的10％上升到终值的90％所需的时间；对有振荡的系统，可定义为从0到第一次达到终值所需的时间。

[3]峰值时间：阶跃响应越过终值达到第一个峰值所需的时间。

[4]调节时间：阶跃响应到达并保持在终值的±5％误差带内所需的最短时间。

[5]超调量%：峰值超出终值的百分比。

二、一阶系统的时间响应及动态性能

1、一阶系统传递函数标准形式及单位阶跃响应

2、一阶系统动态性能指标计算

（1）一阶系统的单位阶跃响应如下图所示，响应时单调的指数上升曲线，根据调节时间的定义，有

        解得

（2）一阶系统的典型响应：

（3）系统对某一输入的微分/积分的响应，等于系统对该输入信号的响应的微分/积分，这是线性定常系统的重要性质，对任意阶线性定常系统均适用。

（4）举例：

三、二阶系统的时间响应及动态性能

1、二阶系统传递函数标准形式及分类

2、过阻尼（临界阻尼）二阶系统动态性能指标计算

3、欠阻尼二阶系统动态性能指标计算

（1）欠阻尼二阶系统的极点可用下图所示的两种形式表示。

（2）欠阻尼二阶系统的单位阶跃响应与单位脉冲响应：

（3）欠阻尼二阶系统动态性能指标计算：

（4）最佳阻尼比：

（5）典型欠阻尼二阶系统动态性能、系统参数及极点分布之间的关系：

（6）举例：

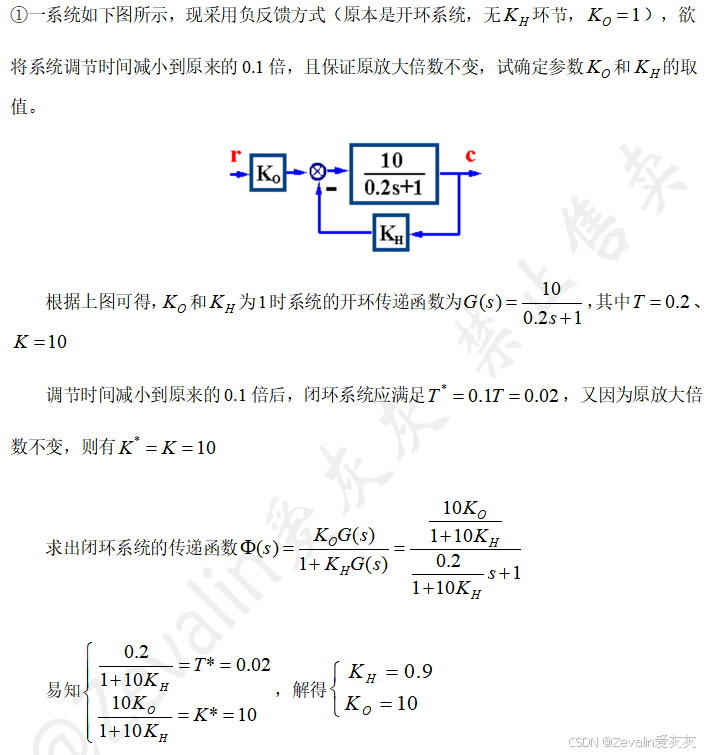
①一控制系统结构图如下图所示。

②一二阶系统的结构图及单位阶跃响应如下图所示，试确定系统参数、、的值。

③对一个典型欠阻尼二阶系统，要求如下，试确定满足要求的系统极点分布范围。

        

4、改善二阶系统动态性能的措施

（2）举例：

5、附加闭环零、极点对系统动态性能的影响

（1）对于一个系统的闭环传递函数，其分母决定了它的闭环极点，分子决定了它的闭环零点。

（2）附加闭环零点不会影响闭环极点，因而不会影响单位阶跃响应中的各模态，但它会改变单位阶跃响应中各模态的加权系数，由此影响系统的动态性能。附加闭环零点会使系统的峰值时间提前，超调量增加，如果它越靠近虚轴，这种影响就越强烈。

（3）附加闭环极点不会影响闭环零点，它不会改变单位阶跃响应中各模态的加权系数，但会影响单位阶跃响应中的各模态，由此影响系统的动态性能。附加闭环极点会使系统的峰值时间延后，超调量减少，如果它越靠近需轴，这种影响就越强烈。