一、耦合器模型
1、弱耦合电感模型深入推导
(1)下图所示的是弱耦合电感的磁元件模型,其中左右的区别为参考点的选取不同,左边是对称性的(常用),右边是非对称性的。
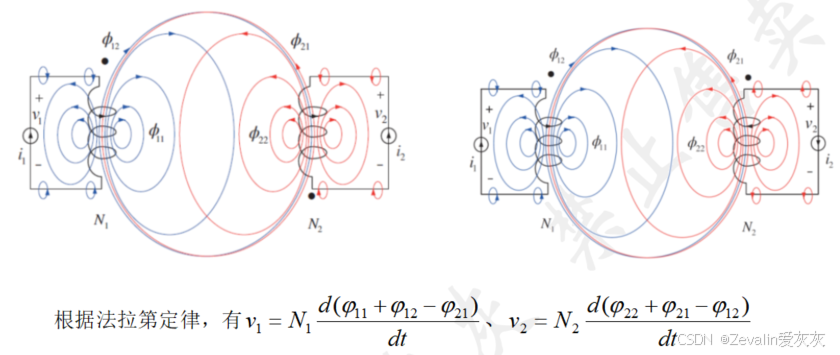
(2)感应式电能传输(Inductive Power Transfer)的基本原理:
①根据安培定律,源端(Tx)线圈产生随时间变化的磁通量,再根据法拉第定律,负端(Rx)线圈的磁通量变化,产生感应电压。
②当耦合电感负端空载时,只有源端向负端提供的感应电压;当耦合电感负端带载时,负端也会向源端提供感应电压。
③能量从源端线圈输入并被负端线圈获取,因此,无限电能是通过线圈传输的。
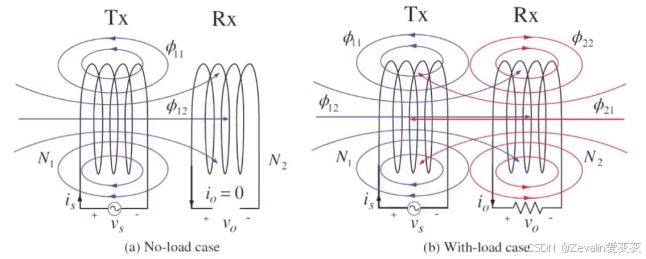
(3)电感的定义:

(4)弱耦合电感的数学模型推导:
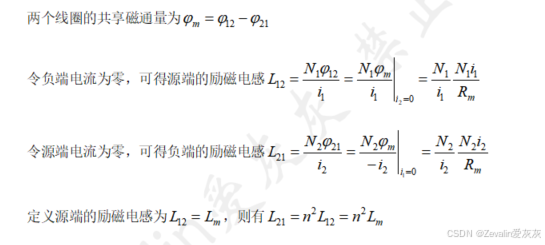
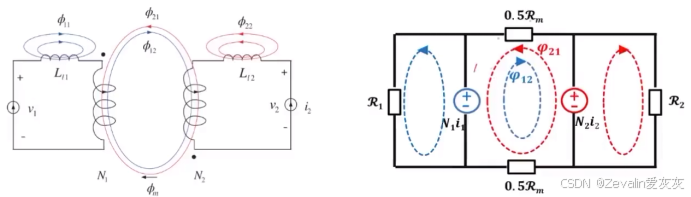
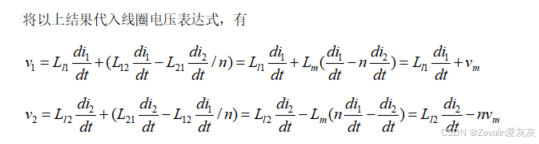

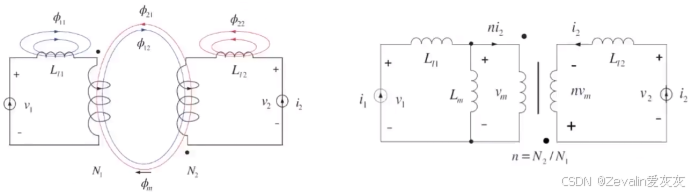
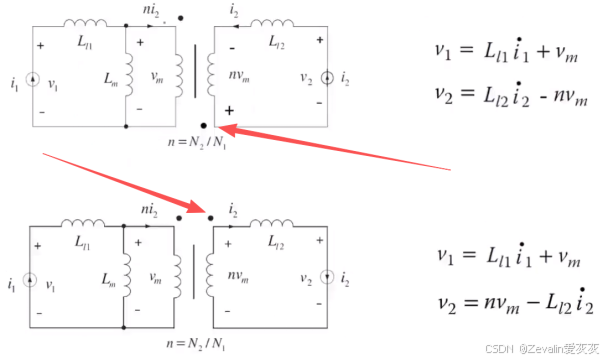
定义的参考点位置不同,线圈电压的表达式也就不同
定义耦合系数K,当其为1时认为耦合是理想的,否则若小于1,则存在漏感,由此可推导出M模型,其中M为互感
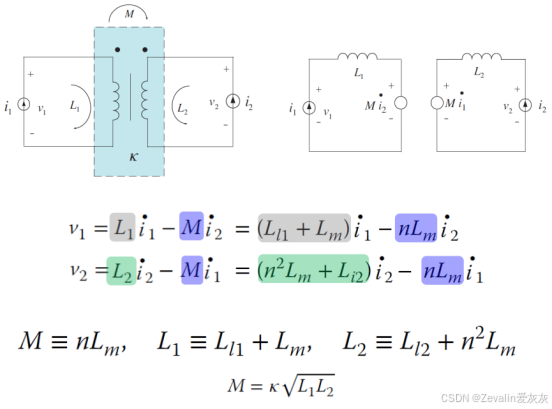
同理,经过一系列数学分析,可以推导出非隔离型T模型

弱耦合电感可以根据输入端和输出端的电感求得一个“等效匝数比”,即,然后分别对源端和负端做开路处理,以求得两边的等效输入阻抗,那么弱耦合电感还可以借用变压器的等效模型表示(隔离型T模型),如下图所示
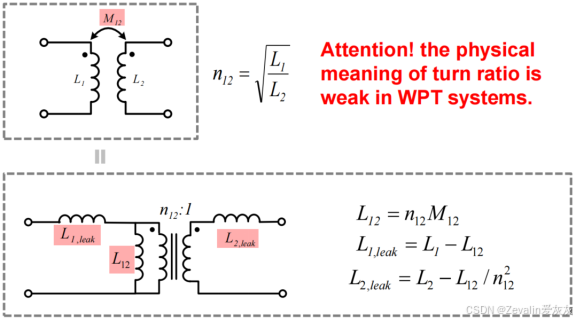
隔离型T模型有考虑匝数比,它经过一系列数学运算后,可以转化为考虑匝数比的非隔离型T模型,相比于前面介绍的非隔离型T模型,它不涉及量纲的转化,运算更加方便
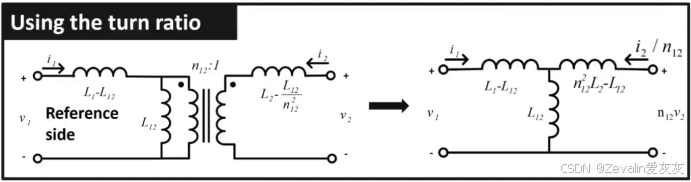
2、耦合器模型深入推导
(1)对于下图所示的N端口网络,首先分析其存在的“物质”数量,其存在N个自感与N(N-1)/2个互感,因此描述该系统至少需要N(N+1)/2个独立变量。
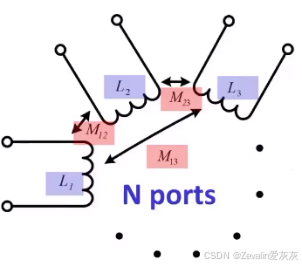
(2)当网络中的端口数量增加,达到至少4个端口时,已经很难甚至无法使用T模型对其进行等效,对此需要另寻方法。
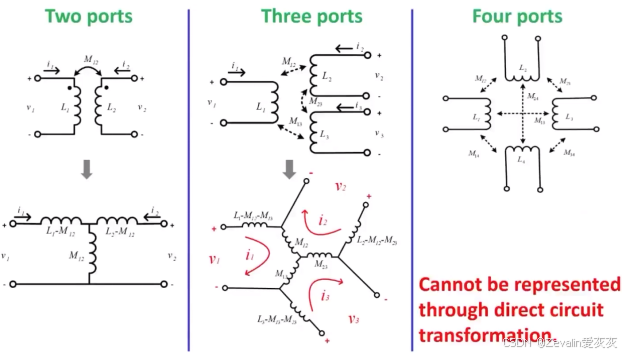
(3)对此提出另一种数学模型(悬臂模型),它在隔离型T模型的的基础上将输出侧的电感等效至输入侧,当然,相应地需要对等效匝数比新设计独立参数,这个等效匝数比已经不是物理意义上的匝数比了,当互感发生变化时,所有参数都会发生相应改变。
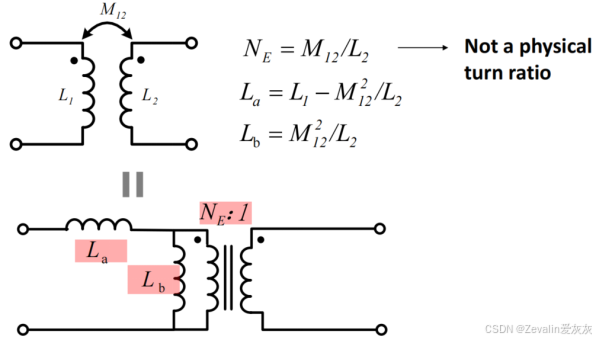
如果这个模型放在LLC谐振变换器中,很难使用传统方法分析LLC谐振变换器的性能
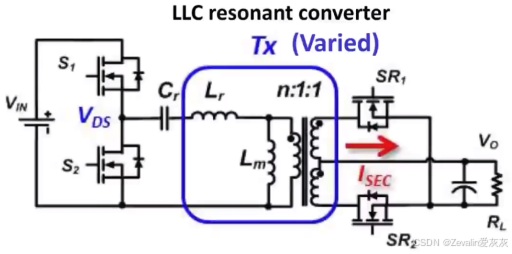
不过,这个模型为N端口网络的数学模型等效提供了可能,在不改变伏安关系和独立参数数量的情况下能够充分表征原始系统,只是电路的复杂度可能会显著增加,因此,该模型也是不适用多接收端网络的
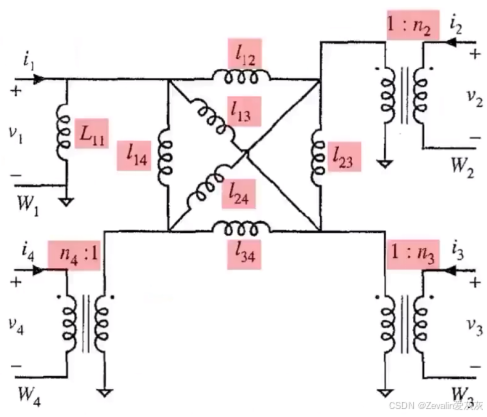
(4)每个端口都有电流与电压两个状态变量,它们往往是比较固定的,对此考虑不采用变压器模型和T模型,而是利用比较固定的状态量减少变量个数。

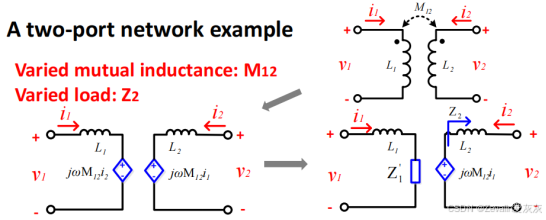
将该结论延伸至多端口网络,可得下图所示结论,其中为所有接收端线圈对输入端产生负载效应的等效
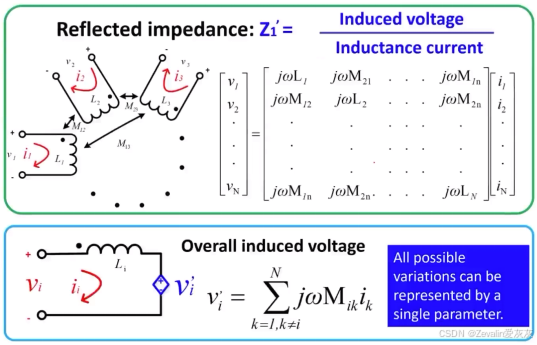
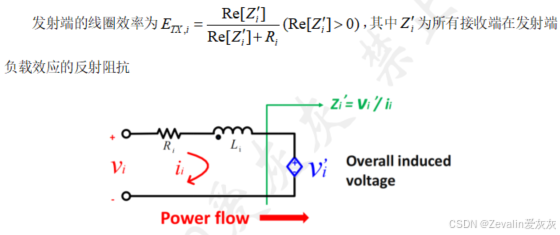
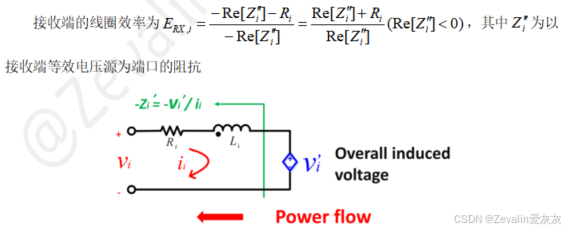
当然,一个线圈它可以是发射器,也可以是接收器,这个没有绝对的说法,需视情况而定
二、耦合器结构
1、耦合线圈的功率传输能力表示
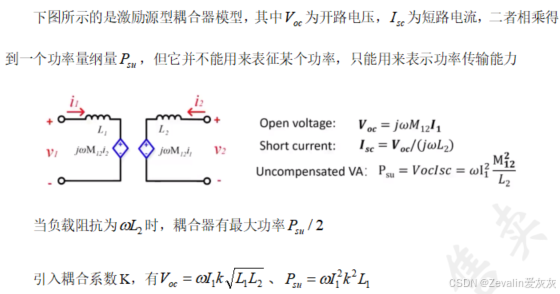
2、强耦合实现
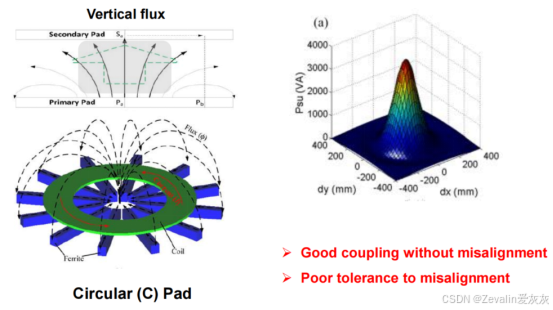
(1)发射端使用单线圈实现强耦合(尽量大):
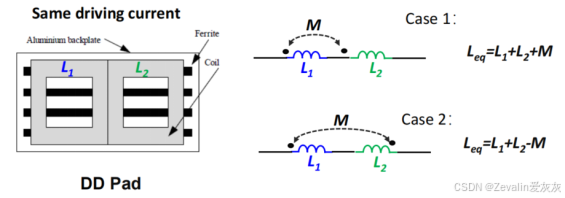
(2)发射端使用多线圈实现强耦合(尽量大):
①两个线圈并列排布,通以反向的电流,以增大输出至负端的磁通量(变化率)。
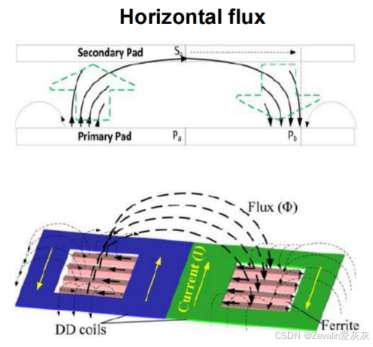
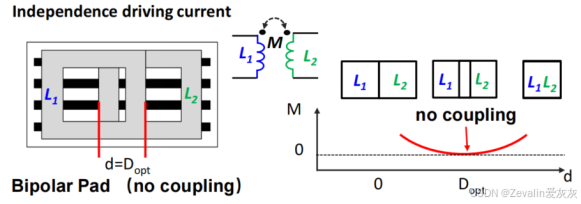
②当两个线圈同轴重叠放置时,通以同向的电流,存在一个最佳距离d,使得线圈间的互感为零,从而消除交叉耦合(互感为零),此时,每个线圈自身的磁通量(变化率)在输出端达到最大值,实现了最优的磁能传输或信号输出效率。
三、补偿网络
1、缺少补偿引起的问题
当缺少补偿网络时,负端耦合器的本体的电感将会获得较大的分压,这将导致输出到负载上的电压非常小
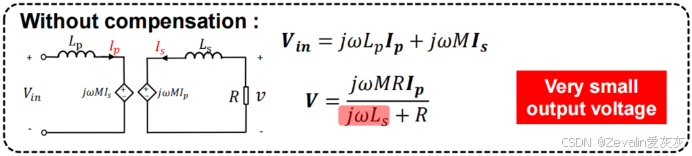
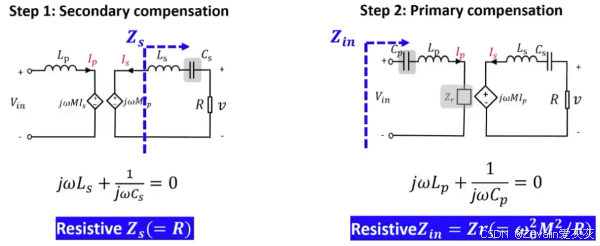
2、四种基本补偿网络组合
(1)为了解决负端耦合器的本体的电感获得较大分压的问题,有如下方法:
①在负端串联一个电容,其与耦合器本体的负端电感构成谐振腔,这样负端阻抗将呈纯阻性,反射到源端的反射阻抗也是纯阻性的。
②再在源端串联一个电容,其与耦合器本体的源端电感构成谐振腔,这样就能把耦合器引起的无功功率全部消除。
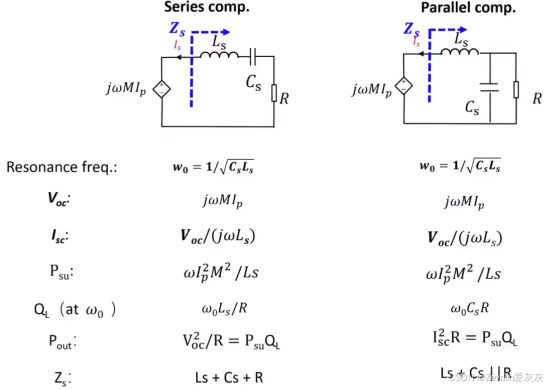
(2)以上使用的是串联补偿网络(串联电容),同样地,也有并联补偿网络(并联电容)。
(3)由于补偿网络在源端和负端都需嵌入,按照排列组合的思想,应有四种不同的补偿方式,如下图所示,为了增强负端的电压利用率,必须有

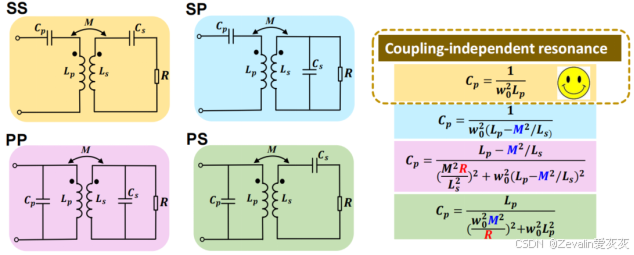
其中双串联(SS型)补偿方式是独立谐振的,也就是说,负端谐振腔的设计与源端谐振腔的设计互不影响,且源端谐振腔的设计不受负载影响
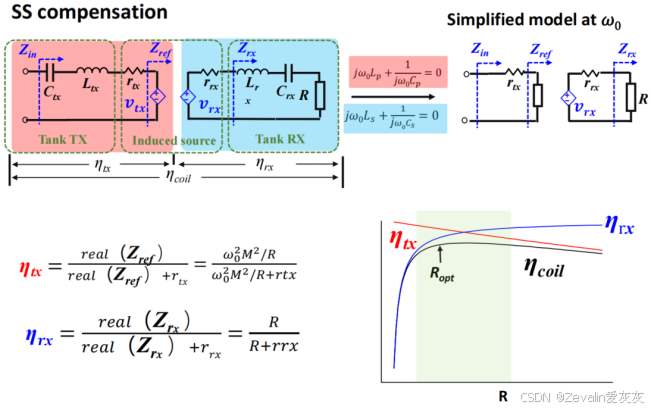
3、SS型补偿
(1)下图所示的是使用SS型补偿耦合线圈的电压增益曲线,它存在两个频率点,工作在任一一个点上时其电压增益恒为1,即与负载无关,是恒压源输出点,而它中间还有一个电压增益峰值点,工作在该点上时输入端谐振腔和输出端谐振腔发生谐振,是恒流源输出点。
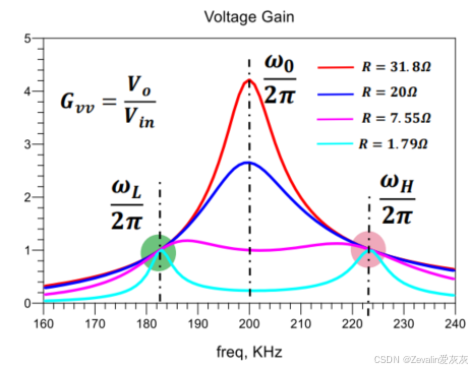
(2)恒压源输出点的求解:
下图所示的是使用SS型补偿的耦合线圈的拓扑
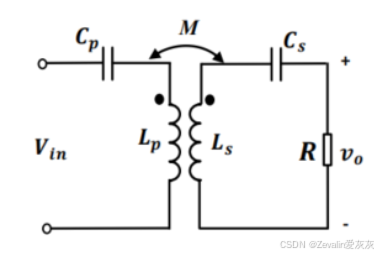
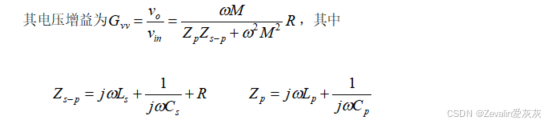
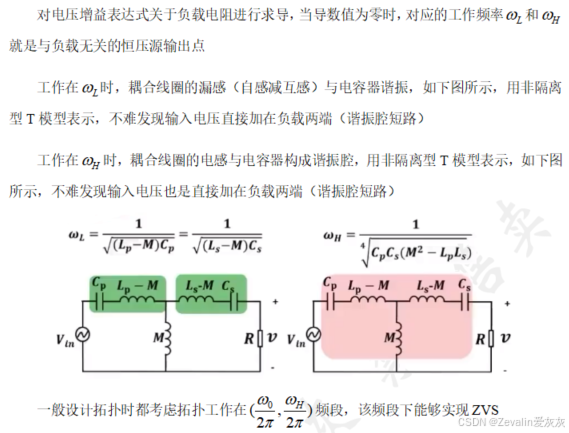
(3)由于恒压源工作点与互感相关,只要耦合系数发生变化,互感也将受到影响,那么恒压源工作点的频率也会相应地产生偏移。
4、SP型补偿
(1)下图所示的是使用SP型补偿耦合线圈的电流增益曲线,它存在两个频率点,工作在任一一个点上时其电流增益恒定,即与负载无关,是恒流源输出点,而它中间还有一个电流增益峰值点,工作在该点上时输入端谐振腔和输出端谐振腔发生谐振,是恒压源输出点。
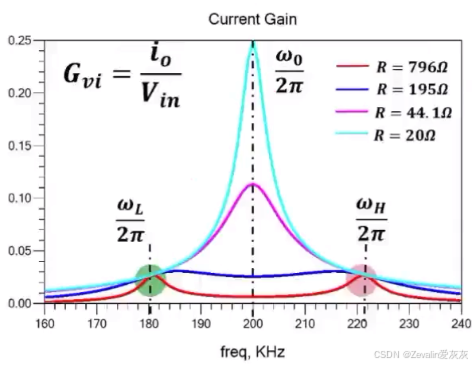
(2)恒流源输出点的求解:
下图所示的是使用SP型补偿的耦合线圈的拓扑
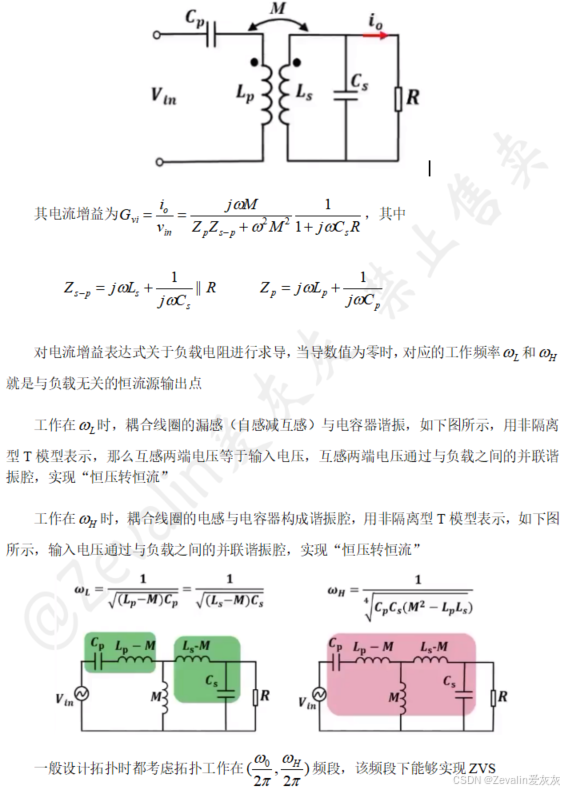
(3)由于恒流源工作点与互感相关,只要耦合系数发生变化,互感也将受到影响,那么恒流源工作点的频率也会相应地产生偏移。
5、LC-S补偿
(1)下图所示的是使用LC-S补偿的耦合线圈的拓扑,其中C1可等效为两个并联的电容。
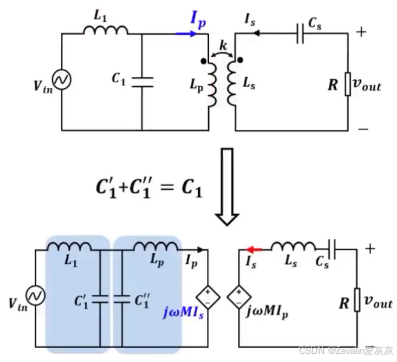
(2)下图所示的是使用LC-S补偿的耦合线圈的电流增益曲线,其存在一个工作点,能够同时实现最大程度的减少无功功率、工作点频率不会随耦合系数(或者说互感)的改变而改变、电流增益与负载无关,该点的频率为
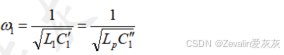
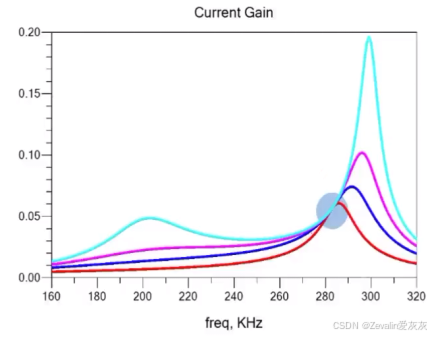
工作在这个恒流源输出点时,源端LCL(C拆解为两个电容后就是LCCL)构成两个并联谐振腔,输入电压经过两级并联谐振腔后仍是一个“钳位电压”(输入电压经过一级并联谐振腔后“钳位”并联支路电流,并联支路电流再经过一级并联谐振腔后“钳位”串联支路电压),也就是说,是不随负载的改变而改变的,它仅随输入电压变化,那么不难得出,
也仅随输入电压变化,与负载无关
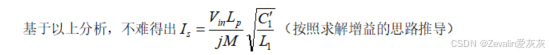
6、双边LCC补偿
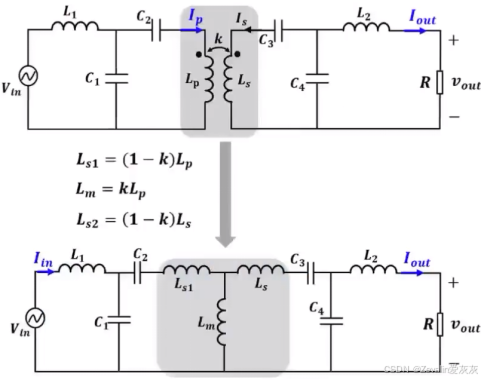
(1)下图所示的是使用双边LCC补偿的耦合线圈的拓扑,其中耦合电感可使用非隔离型T模型简化。
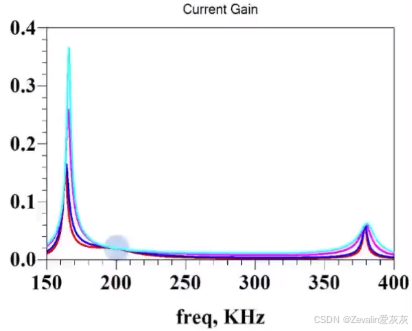
(2)下图所示的是使用双边LCC补偿的耦合线圈的电流增益曲线,其也存在一个工作点,能够同时实现最大程度的减少无功功率、工作点频率不会随耦合系数(或者说互感)的改变而改变、电流增益与负载无关。

7、补偿网络家族
(1)在为耦合线圈设计补偿网络时,可以将其分解为三个部分——输入端补偿网络、耦合电感、输出端补偿网络,其中耦合电感可用受控电压源模型等效,输入电流对输出端电压形成钳位,输出电流对输入端电压形成钳位。
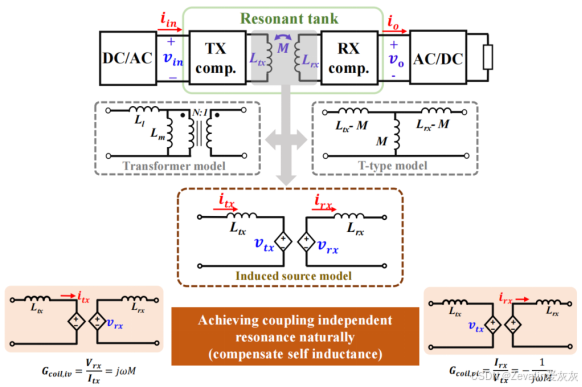
(2)输入端的补偿网络设计和输出端基本对称,下面以输出端为例进行说明。
①输入端需要构建谐振腔,如果谐振腔由两个元件组成,那么网络右端必须串联电感,这个电感来源于耦合线圈的输入侧漏感,二元件通过排列组合能形成8种谐振腔,符合需求的只有2个。
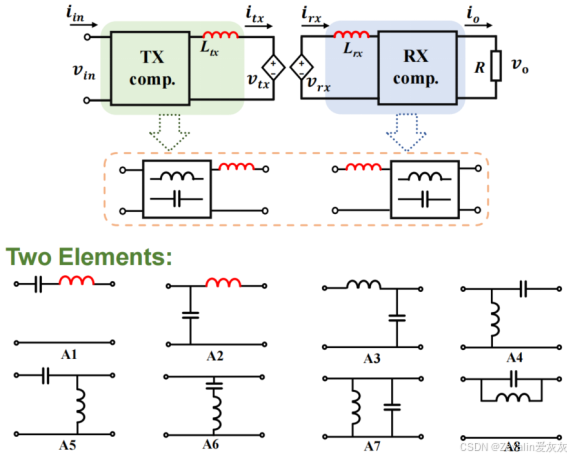
③继续升级,如果谐振腔由三个元件组成,且网络右端必须串联电感,那么二元件排列组成的8种谐振腔中,在被淘汰的6种右侧各串联一个电感,即可形成符合需求的三元件谐振腔(在未被淘汰的二元件谐振腔右侧串联一个电感无意义,两个串联的电感等效为一个大电感),此外,还需考虑CCL的情况,CCL通过排列组合,能形成2种符合需求的谐振腔。
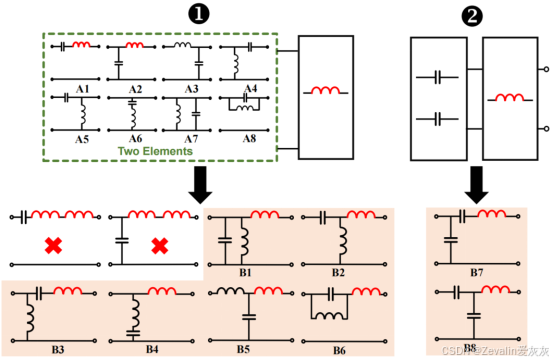
④同样地,继续升级,可得到30种符合需求的四元件谐振腔。
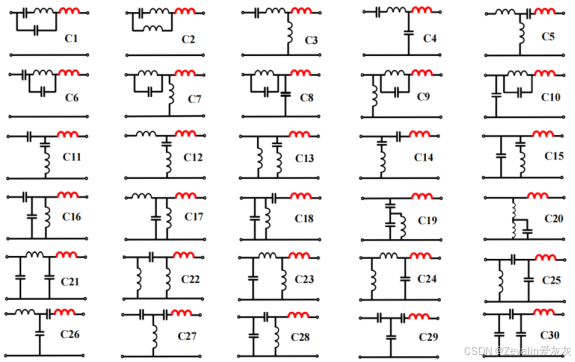
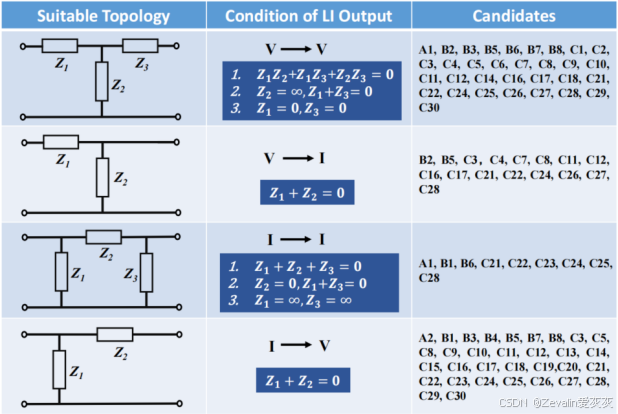
(3)不同负载无关增益设计对应的补偿网络拓扑结构选取及网络中的阻抗关系(根据谐振腔谐振时所产生的“钳位”效应理解即可):
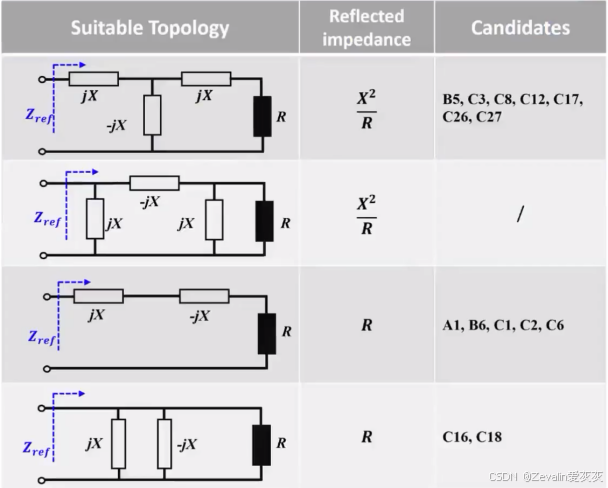
(4)纯阻性阻抗(零相位)设计对应的补偿网络拓扑结构选取及对应的反射阻抗:
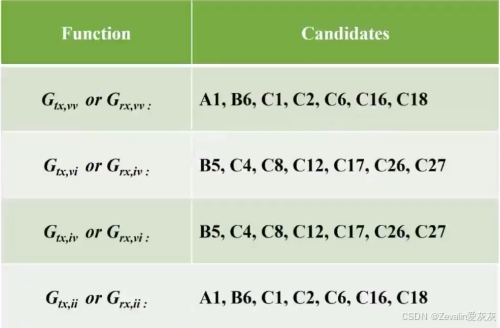
(5)综上,能实现负载无关输出、阻抗零相角、耦合独立共振的补偿网络如下:
四、最优效率
1、寄生电阻对效率的影响
(1)考虑寄生电阻后,带补偿网络的耦合线圈的效率如下所示。
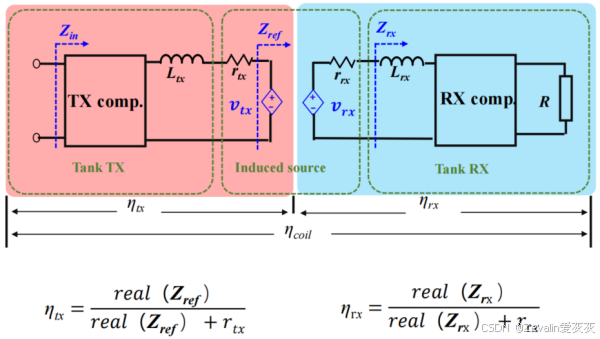
(2)以电压增益负载无关网络为例,不考虑寄生电阻与考虑寄生电阻时电压增益的差异:
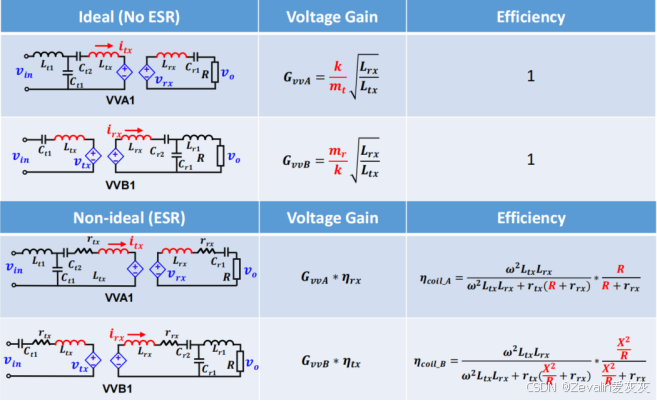
(3)以SS型网络为例,当其工作在恒压源输出点时,输入端的电容和电感产生谐振,输出端的电容和电感产生谐振,因此源端的电压能够直接“钳位”负载电压,可以很容易地计算出其效率。
(4)以上计算是建立在负载为纯阻性的前提下的,如果负载的阻抗虚部不为零,这将降低源端的效率。
2、效率最大化
(1)为了方便表征耦合线圈本身的效率,定义三个品质因数:
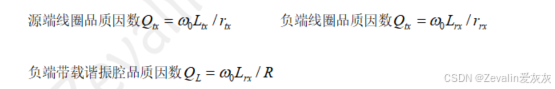
(2)将品质因数代入先前求出的效率表达式,有

五、CPT(电容式电力传输)
1、耦合电感与耦合电容的差别与联系
(1)耦合电感通过磁场传递能量(IPT),因为使用了磁芯,所以其元件尺寸较大,对周围的金属敏感,另外还有涡流损耗,这些都是不好的特性。
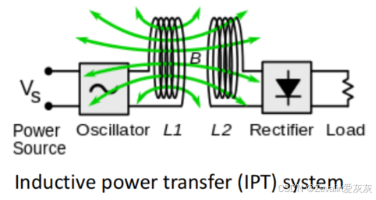
(2)耦合电容通过电场传递能量(CPT),其涡流损耗可忽略不计,成本低、轻量化,还可在金属介质中传输电力,具有更好的错位性能。
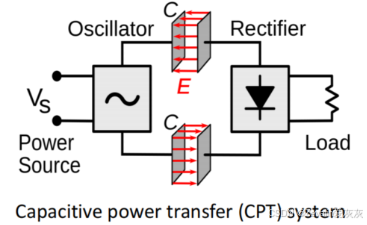
2、耦合电容的分析方法
(1)耦合电容的分析方法和耦合电感是高度对称的,它同样能转化为受控源模型进行分析,不同的是,耦合电感对应的是受控电压源模型,耦合电容对应的是受控电流源模型。
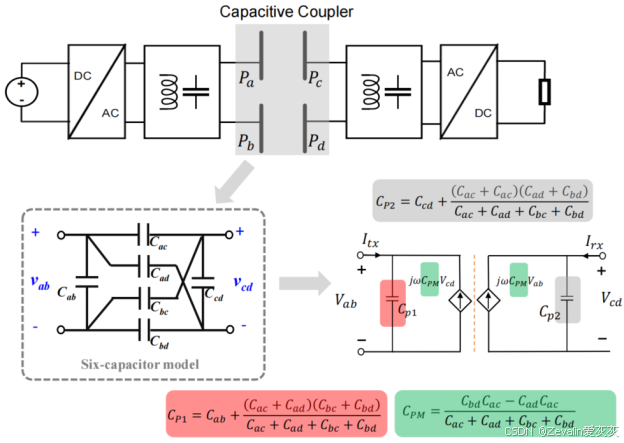
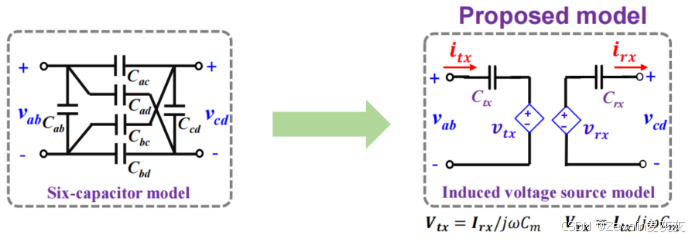
(2)根据诺顿定理,耦合电容对应的受控电流源模型也可转化为受控电压源模型。






















 1021
1021

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










