题意是告诉这么个函数: ,以及相关定义域
,以及相关定义域 .
,输入p,k,问可以找出多少函数满足条件
.
,输入p,k,问可以找出多少函数满足条件
题解:Now assume that k ≥ 2, and let
m be the least positive integer such that  This is called the \emph{order} of
This is called the \emph{order} of  First, plug in
x = 0 to find that
First, plug in
x = 0 to find that 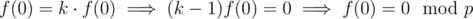 as
p is prime, and
as
p is prime, and  . Now for some integer
. Now for some integer
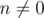 , choose a value for
f(n). Given this value, we can easily show that
, choose a value for
f(n). Given this value, we can easily show that
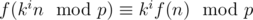 just by plugging in
x = ki - 1n into the functional equation and using induction. Note that the numbers
n, kn, k2n, ..., km - 1n
are distinct
just by plugging in
x = ki - 1n into the functional equation and using induction. Note that the numbers
n, kn, k2n, ..., km - 1n
are distinct  , since
m is the smallest number such that
, since
m is the smallest number such that  .
Therefore, if we choose the value of f(n), we get the value of
m numbers (
.
Therefore, if we choose the value of f(n), we get the value of
m numbers ( ). Therefore, if we choose
f(n) of
). Therefore, if we choose
f(n) of  integers
n, we can get the value of all
p - 1 nonzero integers. Since f(n) can be chosen in
p ways for each of the
integers
n, we can get the value of all
p - 1 nonzero integers. Since f(n) can be chosen in
p ways for each of the  integers,
the answer is
integers,
the answer is  . 经过这一系列推导得出
. 经过这一系列推导得出 这个答案。。。
这个答案。。。
#include <cstdio>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <vector>
#include <set>
#include <list>
#include <queue>
#include <map>
#include <stack>
using namespace std;
#define L(i) i<<1
#define R(i) i<<1|1
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-9
#define maxn 1000010
#define MOD 1000000007
char s[maxn];
long long p,k;
long long mod_pow(long long a,long long b,long long p)
{
long long ans = 1;
while(b)
{
if(b&1)
ans *= a;
ans %= p;
b >>= 1;
a *= a;
a %= p;
}
return ans;
}
int main()
{
int t;
//scanf("%d",&t);
while(scanf("%I64d%I64d",&p,&k) != EOF)
{
if(k == 0)
printf("%I64d\n",mod_pow(p,p-1,MOD));
else if(k == 1)
printf("%I64d\n",mod_pow(p,p,MOD));
else
{
int m = 0;
long long ans = 1;
while(1)
{
ans *= k;
ans %= p;
m++;
if(ans == 1)
break;
}
printf("%I64d\n",mod_pow(p,(p-1)/m,MOD));
}
}
}








 本文探讨了一道关于数论函数的问题,通过定义特定的数论函数并利用其性质,结合数学归纳法,最终推导出求解该函数在特定条件下计数的方法。
本文探讨了一道关于数论函数的问题,通过定义特定的数论函数并利用其性质,结合数学归纳法,最终推导出求解该函数在特定条件下计数的方法。
















 1757
1757

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








