Jzzhu and Chocolate（CF-449A）

Problem Description

Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:

each cut should be straight (horizontal or vertical);
each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
each cut should go inside the whole chocolate bar, and all cuts must be distinct.
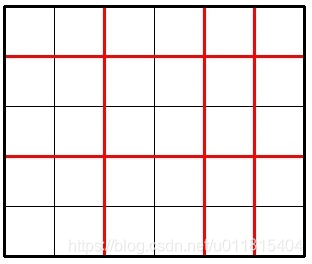
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.

Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactly k cuts? The area of a chocolate piece is the number of unit squares in it.

Input

A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).

Output

Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.

Examples

Input

3 4 1

Output

6

Input

6 4 2

Output

8

Input

2 3 4

Output

-1

Note

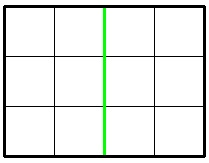
In the first sample, Jzzhu can cut the chocolate following the picture below:

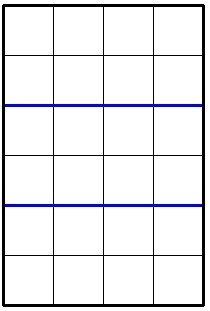
In the second sample the optimal division looks like this:

In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.

题意：输入 n，m，k，代表一个 n*m 的矩阵要切 k 次，问切完后最小的单元格的最大值

思路：

假设横向切了 x-1 次，纵向切了 y-1 次，那么横着就分为 x 份，纵着就分为 y 份

于是结果即为：res=(n/x)*(m/y)，而题目所给范围为：1<=x<=n，1<=y<=m，(x-1)+(y-1)=k

显然：(n+m-2)<k 时无解，(n+m-2)=k 时值为 1

可以考虑先枚举 n/x 的值，那么对于固定的取值，可以选出最大的 x，使得此时 m/y 最大；然后再枚举  n/y 的值，那么对于固定的取值，可以选出最大的 y，使得此时 n/x 最大，最后取两者最大值即可

我们将 y=k+2-x 代入 res=(n/x)*(m/y) 中可得到分母是一个二元函数：-y^2+2*y+ky，那么要让原式最大，就要让分母最小，因此不需枚举 x、y 的值，直接令 x、y 分别最小即可

Source Program

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define PI acos(-1.0)
#define E 1e-9
#define INF 0x3f3f3f3f
#define LL long long
const int MOD=1e9+7;
const int N=10+5;
const int dx[]= {-1,1,0,0};
const int dy[]= {0,0,-1,1};
using namespace std;
int main(){
    int n,m,k;
    cin>>n>>m>>k;

    LL res=0;
    if( (n-1)+(m-1)<k )//刀数多于切口数
        res=-1;
    else if( (n-1)+(m-1)==k )//刀数等于切口数
        res=1;
    else{
        LL x=min(n-1,k);//令x最小
        res=max( res, (n/(x+1))*(m/(k+1-x)) );
        LL y=min(m-1,k);//令y最小
        res=max( res, (m/(y+1))*(n/(k+1-y)) );
    }
    cout<<res<<endl;
    return 0;
}