Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
- each cut should be straight (horizontal or vertical);
- each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
- each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
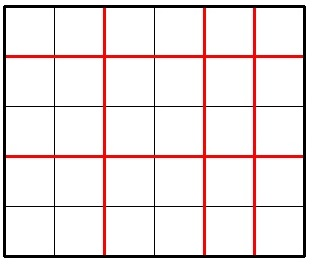
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactlyk cuts? The area of a chocolate piece is the number of unit squares in it.
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
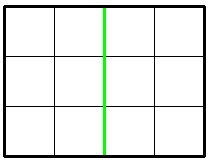
3 4 1
6
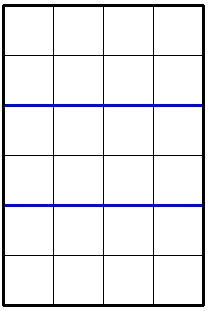
6 4 2
8
2 3 4
-1
In the first sample, Jzzhu can cut the chocolate following the picture below:
In the second sample the optimal division looks like this:
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
题意:
给出 n,m(1 ~ 10 ^ 9),k(2 X 10 ^ 9)代表给出一个 N * M 个的格子矩阵,后要求切 K 刀,使得出的最小方块的格子尽量大。输出这个格子数。
思路:
贪心。尽量多的横切或者尽量多的纵切。
AC:
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
int main() {
ll n, m, k;
scanf("%I64d%I64d%I64d", &n, &m, &k);
if (n + m - 2 < k) printf("-1\n");
else {
ll maxn = 0;
if (n > k) maxn = max(maxn, m * (n / (k + 1)));
if (m > k) maxn = max(maxn, n * (m / (k + 1)));
if (n <= k) maxn = max(maxn, m / (k - (n - 1) + 1));
if (m <= k) maxn = max(maxn, n / (k - (m - 1) + 1));
printf("%I64d\n", maxn);
}
return 0;
}





 本文探讨了如何通过切巧克力的策略,使切出的最小巧克力块面积尽可能大。通过贪心算法,我们找到了在给定切割次数下,实现最大最小块面积的方法。
本文探讨了如何通过切巧克力的策略,使切出的最小巧克力块面积尽可能大。通过贪心算法,我们找到了在给定切割次数下,实现最大最小块面积的方法。
















 1311
1311

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








