动手学深度学习 - 17. 强化学习 - 17.1 马尔可夫决策过程（MDP）

---

🚀 动手学深度学习 - 17.1 马尔可夫决策过程（MDP）

理论 + 实战双视角，带你掌握强化学习建模的起点

---

🎯 前言：为什么我们需要 MDP？

在强化学习中，Agent 想要学习如何在环境中做决策，找到能获得最大长期奖励的策略。我们需要一个严谨的框架来定义“状态-动作-奖励-转移”，这就是 马尔可夫决策过程（MDP）。

---

1️⃣ MDP 的定义

马尔可夫决策过程（MDP） 是一个五元组：

符号	含义
$\mathcal{S}$	状态空间，Agent 可能处于的所有状态
$\mathcal{A}$	动作空间，Agent 可执行的所有动作
$P(s'	s,a)$
$R(s,a)$	奖励函数，执行 $a$ 后从 $s$ 获得的奖励
$\gamma$	折扣因子，用于计算长期回报

🧠 我的理解：MDP 就像是为 RL 设计的一套世界规则，把每一步决策都纳入数学建模，同时提供了一个“试错反馈”的机制。

---

📷 图示：GridWorld 示例

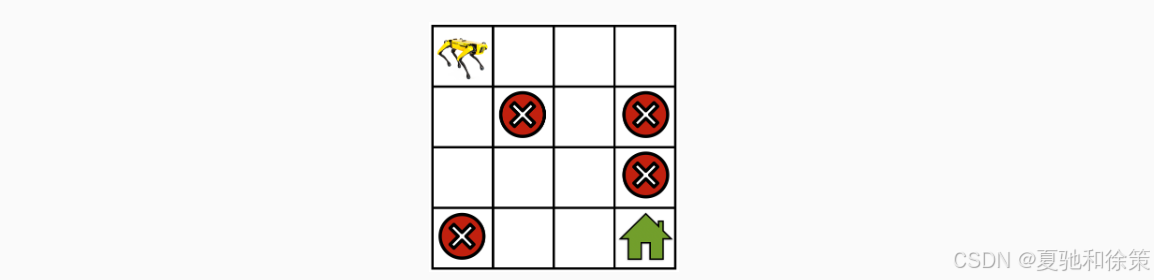
机器人需要从起点移动到目标（房子🏠），同时避开红色叉（陷阱❌）。
这就是一个典型的 MDP 建模场景：

• 状态：格子坐标

• 动作：上下左右移动

• 奖励：到终点 +10，掉陷阱 -10，其余动作 -1

• 转移：可能受风/概率随机影响

---

2️⃣ 回报与折扣因子

轨迹（trajectory）是一个序列：

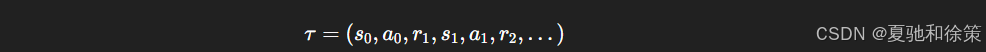
✅ 总回报（Return）：

如果轨迹无限长（如不停绕圈），总回报可能发散。

✅ 引入折扣因子 $\gamma$：

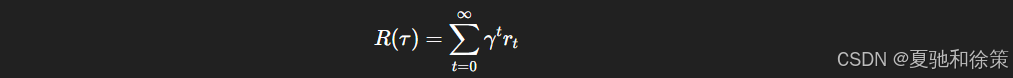
• $\gamma$ 越小：更看重眼前奖励（短视）

• $\gamma$ 越大：更看重长远目标（远见）

🔧 工程经验：

• DQN/PPO 中常设 $\gamma=0.99$

• 对于像 GridWorld 这样“终点明确”的任务，使用 $\gamma$ 可以防止绕圈，促使模型快速达成目标

---

3️⃣ 马尔可夫假设的讨论

🧩 马尔可夫性定义：

状态转移只与当前状态和当前动作有关：

🎯 也就是说，历史信息通过“当前状态”完全封装了。

🚧 非马尔可夫例子：

如果一个机器人的位置不仅与当前位置、动作有关，还与“过去的速度/加速度”有关，则该系统不是马尔可夫的，除非我们把“位置 + 速度”都塞进状态空间！

✅ 结论：是否马尔可夫，取决于你怎么定义状态空间。

---

4️⃣ 小结（from 17.1.4）

概念	解释
MDP 五元组	$(\mathcal{S}, \mathcal{A}, P, R, \gamma)$
马尔可夫性	下一个状态只依赖当前状态和动作
强化学习目标	找到策略 $\pi$ 最大化期望累计回报
折扣回报公式	$\sum_t \gamma^t r_t$，使得未来奖励有界

---

5️⃣ 实战练习设计（from 17.1.5）

🚙 练习一：MountainCar

• 状态空间：$(position, velocity)$

• 动作空间：${左推、右推、不动}$

• 奖励函数：

  • 每一步 -1（鼓励尽快爬上山）

  • 抵达终点后 episode 结束

🧠 经验：此任务 reward sparse，训练困难，建议使用 DDPG/PPO 等策略优化方法。

---

🕹️ 练习二：Pong（Atari 游戏）

• 状态空间：图像帧（或抽象 paddle+ball 的位置速度）

• 动作空间：${上、下、不动}$

• 奖励函数：

  • 赢球 +1

  • 输球 -1

  • 其他时间 0

💡 建议搭配 DQN + CNN 特征提取模块 + ReplayBuffer 实现效果更佳。

---

✅ 总结一句话

马尔可夫决策过程是强化学习建模的根基，只有理解它，才真正进入了 RL 世界的大门。

---