6.3 Math类与Random类

思维导图：

 

 

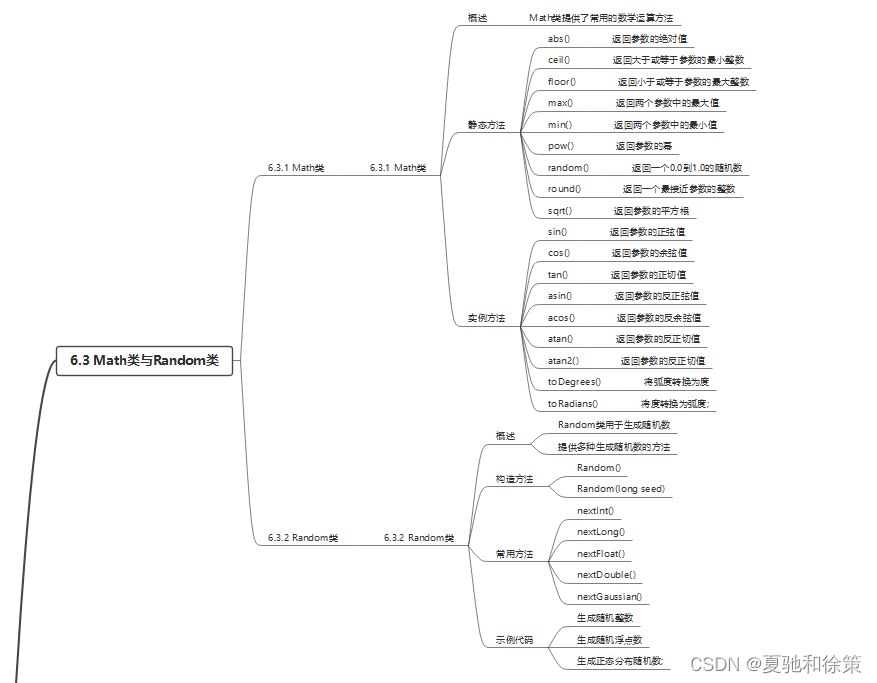
6.3 Math类与Random类

6.3.1 Math类

• 定义与特性:

  • Math类是一个工具类，专用于科学计算。
  • 包含多种计算方法，如平方根、绝对值和随机数生成。
  • 无法实例化（构造方法为private）。
  • 所有方法为静态，通过类名直接调用。
  • 包含静态常量PI（π）和E（e）。

• 常用方法:

  • abs(double a): 计算绝对值。
  • sqrt(double a): 计算平方根。
  • ceil(double a): 计算大于等于a的最小整数。
  • floor(double a): 计算小于等于a的最大整数。
  • round(double a): 四舍五入。
  • max(double a, double b): 返回最大值。
  • min(double a, double b): 返回最小值。
  • random(): 生成0.0至1.0的随机数。
  • sin(double a): 返回正弦值。
  • asin(double a): 返回反正弦值。
  • pow(double a, double b): 计算a的b次幂。

示例应用

• 示例代码（Example15.java）展示了Math类方法的使用。
  • 如：计算-10的绝对值、求5.6的ceil值、求-4.2的floor值等。
  • 运行结果展示了各种计算的输出。

总结

• 这一节深入探讨了Math类的多种功能，提供了一个强大的工具集合，用于处理各种数学运算和数值计算。通过示例代码，可以看到这些方法在实际编程中的应用。

 

6.3.2 Random类

定义与构造方法

• Random类: 用于生成指定范围的随机数。
• 构造方法:
  1. Random(): 使用当前系统时间作为种子创建Random对象。
  2. Random(long seed): 使用指定种子创建Random对象。

特性与应用

• 种子的作用:
  • 使用无参构造时，每个Random对象的种子是随机的，产生不同的随机数序列。
  • 使用带种子的构造方法，可使多个Random对象产生相同的随机数序列。

示例代码

• Example16.java (使用无参构造):

  • 创建Random对象，不传入种子。
  • 生成[0,100)区间的10个随机整数。
  • 每次运行结果不同，因为种子是基于当前时间戳。

• Example17.java (使用带种子构造):

  • 创建Random对象，传入固定种子（例如13）。
  • 同样生成[0,100)区间的随机整数。
  • 每次运行结果相同，因为种子固定。

Random类方法

• 常用方法:
  • nextBoolean(): 生成布尔类型随机数。
  • nextDouble(): 生成双精度浮点类型随机数。
  • nextFloat(): 生成浮点类型随机数。
  • nextInt(): 生成整型随机数。
  • nextInt(int n): 生成[0,n)区间的整型随机数。
  • nextLong(): 生成长整型随机数。

案例示范

• Example18.java:
  • 展示了使用Random类生成不同类型随机数的方法。
  • 包括生成布尔型、浮点型、双精度浮点型、整型和长整型随机数。

总结

• Random类提供了多种方式来生成不同类型的随机数，是处理随机性需求的有效工具。通过构造方法的不同选择，可以控制随机数序列的重复性，这在测试或特定应用中非常有用。 示例代码清晰展示了如何利用这些方法在实际编程中生成所需的随机数。

 

 我对Math类的理解：

1. abs(double a)

• 用途: 计算任何数（整数或浮点数）的绝对值。
• 使用场景: 在处理数学运算时避免负数的影响，如距离计算。
• 技巧: 直接使用 Math.abs(数值) 即可。
• 错误点: 不要忽视负零（-0.0）的处理，Math.abs(-0.0) 会返回 +0.0。

2. sqrt(double a)

• 用途: 计算数值的平方根。
• 使用场景: 用于几何学计算，比如求斜边长度。
• 技巧: 注意处理负数输入，因为负数的平方根是虚数，Math.sqrt 会返回 NaN。
• 错误点: 尝试对负数调用此方法会导致非数字（NaN）结果。

3. ceil(double a) & floor(double a)

• 用途: ceil 向上取整，floor 向下取整。
• 使用场景: 在需要非小数结果时使用，如分页计算。
• 技巧: ceil 在处理负数时表现与正数不同，例如 Math.ceil(-0.5) 为 -0.0。
• 错误点: 认为 ceil 和 floor 对正负数的处理完全相反。

4. round(double a)

• 用途: 四舍五入。
• 使用场景: 在需要将浮点数转换为最接近的整数时。
• 技巧: round 对半数的处理是向正无穷方向舍入。
• 错误点: 忽略了 round 的舍入规则，例如 Math.round(-1.5) 会得到 -1 而非 -2。

5. max(double a, double b) & min(double a, double b)

• 用途: 返回两个数中的最大值或最小值。
• 使用场景: 在比较操作中确定极值。
• 技巧: 注意处理 NaN，因为任何涉及 NaN 的比较都会返回 NaN。
• 错误点: 认为 NaN 在比较中被视为一个正常值。

6. random()

• 用途: 生成一个 [0.0, 1.0) 范围内的随机浮点数。
• 使用场景: 生成随机数据，如模拟、测试等。
• 技巧: 可以通过乘以范围和加上最小值来生成不同范围的随机数。
• 错误点: 忘记了 random 生成的是一个不包含 1.0 的数。

7. sin(double a), asin(double a), pow(double a, double b)

• 用途: sin 计算正弦值，asin 计算反正弦值，pow 计算幂。
• 使用场景: sin 和 asin 在三角计算中使用，pow 在各种数学运算中。
• 技巧: asin 的输入范围是 [-1, 1]，超出此范围会返回 NaN。
• 错误点: pow 在处理特殊值时（如 pow(0,0)）可能会返回不符合直觉的结果。

总结

在使用 Math 类时，要特别注意方法的输入范围和返回值，特别是在处理极端值和特殊情况（如 NaN 或无穷大/小）时。正确理解每个方法的数学含义和计算规则是有效避免错误的关键。

 

 我对Random类的理解：

1. Random() 和 Random(long seed)

• 用途:
  • Random(): 基于当前时间戳创建随机数生成器。
  • Random(long seed): 使用指定的种子创建随机数生成器。
• 使用场景:
  • 无参构造用于常规的随机数生成。
  • 带参构造用于可重复的随机数生成，如测试或模拟场景。
• 技巧: 使用相同种子的Random对象将产生相同的随机数序列。
• 错误点: 忽略种子的作用，导致在需要可重复结果的场景中不能正确复现随机数序列。

2. nextInt()

• 用途: 生成随机整数。
• 使用场景: 当需要随机整数时，如在游戏、模拟或测试中。
• 技巧: nextInt(n) 生成 [0, n) 范围内的整数。
• 错误点: 错误地认为 nextInt(n) 生成的是 [0, n] 范围内的整数。

3. nextFloat() 和 nextDouble()

• 用途: 生成随机浮点数。
• 使用场景: 当需要[0.0, 1.0)范围内的随机数，如在生成随机百分比时。
• 技巧: 可通过乘以范围和加上最小值来生成不同范围的随机浮点数。
• 错误点: 忽略了结果总是小于1的事实，即无法生成1.0。

4. nextBoolean()

• 用途: 生成随机布尔值。
• 使用场景: 在需要随机的真/假选择时，如模拟抛硬币。
• 技巧: 直接使用，无需额外配置。
• 错误点: 没有特别的误用点，但使用上相对简单直接。

5. nextLong()

• 用途: 生成随机长整数。
• 使用场景: 当需要的随机数范围超出int的范围时，比如在大范围内选择随机时间戳。
• 技巧: 类似于nextInt，但用于更大范围的数值。
• 错误点: 在不需要极大数值范围时误用，可能导致不必要的性能开销。

6. nextInt(int n)

• 用途: 生成 [0, n) 范围内的随机整数。
• 使用场景: 在指定上限的情况下生成随机数，如在数组或列表中随机选取元素。
• 技巧: 理解它生成的数永远不会达到 n。
• 错误点: 忽视范围上限是开放的，即不包括 n。

总结

在使用Random类时，重要的是理解每个方法生成随机数的范围和特性。特别是在边界条件下（如最大值和最小值），了解如何正确使用这些方法可以避免常见错误。合理应用种子可实现结果的可重复性，这在测试和模拟场景中尤为重要。

 

 

 

总结：

Math类

重点

• 提供了一系列用于执行基本数学运算的静态方法，如平方根、绝对值、三角函数等。
• 包含两个重要的常量：PI 和 E。
• 所有方法都是静态的，可以直接通过类名调用，无需创建对象实例。

难点

• 理解并正确使用特定的数学方法，特别是那些涉及到复杂数学概念的方法，如asin、acos、atan等。
• 正确处理特殊值，如NaN（非数字）、无穷大或无穷小值。

易错点

• 错误地处理边界和特殊情况，例如将负数传递给sqrt方法（会产生NaN）。
• 在进行整数和浮点数操作时混淆ceil, floor, 和 round的行为。
• 忽视Math方法在处理极值（如非常大或非常小的数）时的行为。

Random类

重点

• 用于生成不同类型的随机数，包括整数、浮点数、长整数、布尔值等。
• 提供两种构造方法：无参构造和带有种子的构造，后者用于生成可预测的随机数序列。

难点

• 理解和使用种子（seed）来产生可预测的随机数序列。
• 使用Random类生成特定范围或类型的随机数，如生成特定区间的整数或浮点数。

易错点

• 在不需要可重复随机数序列的场景中错误地使用种子。
• 错误理解nextInt, nextFloat, nextDouble等方法的范围，特别是它们的上界（不包括上界本身）。
• 在重复使用Random实例时忽略其内部状态的改变，这会影响后续生成的随机数。

总结

在使用Math和Random类时，关键是要理解各个方法的用途、行为和它们的数学基础。特别是在处理边界值和特殊情况时，正确使用这些方法对于避免常见错误至关重要。对于Random类，正确使用种子以及理解随机数生成范围和概率分布是实现有效和预期内随机数生成的关键。