LOAM SLAM原理之防止非线性优化解退化

1. 概述

LOAM中用于防止非线性优化解退化的方法，指出原始参考代码中出现错误的地方，希望能帮助大家，同时供自己以后参考。

2. 理解

对于SLAM而言，视觉传感器需要纹理信息决定特征点，距离传感器需要空间几何结构信息决定特征点，在特征点缺乏时，状态估计方法会进行退化，为了解决这种退化问题，本文提出了一种在线方法。
处理退化的常用方法有:

• 1）当出现退化时换一种方法;这要求在设计时需要一个备用方法可用
• 2）在状态估计过程中加入人工约束，如恒速模型的约束。即使问题本身是可解决的情况下也会带来不必要的误差。

我们的方法是在原始问题的部分子空间添加约束。原始问题的解可以分为非退化方向和退化方向，在处理问题时，首先确定退化方向，然后将求出原始问题非退化方向的解，对于退化方向的解使用猜测值。在最后的实践算法中，只使用非线性优化解在非退化方向的分量，不考虑退化方向的分量。

正常情况下，约束应该是分布在空间中的多个方向，从各个角度约束解，如下面所示，绿色点表示问题的解，被非退化约束限制在了一个小区域。这样的解就比较准确，约束发生小变化时，解的变化也很小，被限制在一个局部区域，这样的解就是一个比较理想的解。

如果解的约束大多近似平行，那么他们就是退化的方向（蓝色箭头表示的方向），这个时候解在退化方向收到的约束就很差。考虑绝对平行时，解的约束也是一个平行的方向，那么这种情况下的解是需要避免的，如果其中一个约束发生了小的偏移，那么解所在的局部区域会发生较大的变化，这样的解是比较糟糕的解。

我们提出的方法只是线性问题、非线性问题求解的一个小步骤，计算复杂度可以忽略。实验结果表明该方法能够改善环境退化下的位姿解估计结果。

这种方法有点类似可观测子空间、可控子空间的概念。
每次求解时

• 优化解=原始解在非退化方向投影+估计值在退化方向投影（实际算法中可以将退化方向解丢弃，只考虑非退化方向）

考虑方程
$$\underset{x}{\min }{f}^2(x)\text{\hspace{1em}(1)}$$
那么$(1)$为线性方程时可以直接使用奇异值分解SVD、QR分解求解，但是$(1)$为非线性方程时需要进行局部微分转换为求解线性方程，因此线性、非线性问题都可以转换为下面的形式
$$arg\underset{x}{\min }||Ax-b|{|}^2\text{\hspace{1em}(2)}$$
我们的方法将(2)中的每一行看作$x$空间中的一个(超)平面，这些平面约束着$x$（通过方向$A$和位置$b$共同约束得到$x$的解），并研究平面的几何分布来确定退化方向。
做出两个假设：

• 假设在考虑传感器噪声的情况下对矩阵A进行了适当的加权。也就是$(1)$问题的线性加权形式
• 原始问题不受约束，并且在问题非退化时，解由真正的传感器测量值决定。

第一个问题：给定线性化系统$(2)$，确定状态空间中时候存在退化并确定相应的退化方向。在退化的情况下，防止在退化方向上出现错误解。
假设$(3)$的原始解为$x_0$，一开始加入经过$x_0$的任意方向扰动$c$，解并不发生变化

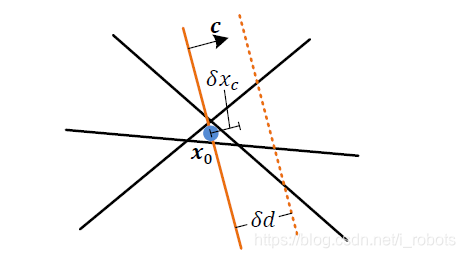
如果扰动$c$相对于$x_0$偏离$\delta d$，那么原始解$x_0$也会偏离$\delta x_c$，因为这个时候的约束区域已经发生了改变。由于扰动$c$的方向任意，因此存在一个原始解的最大偏移，$\delta {x_c}^{\ast }=\underset{c}{\max }{x}_c$
定义1：退化因子$D$
$$D=\frac{\delta d}{\delta {x_c}^{\ast }}\text{\hspace{1em}(3)}$$
现在看一下$D$的含义，也就是

• $\delta d$的扰动导致的影响$\delta x_c$解的偏移量最大，那么这个方向的解最不稳定，因此称这个方向为退化方向。

后面实际应用中会使用阈值来判断退化方向，只有满足一定条件才属于真正的退化方向，解在这个方向的分量并不可靠，因此需要去除或者调整解的这一部分分量。

根据推导可以得出两个结论，具体的推导可以查看原始论文，这里就不再详细推导了。

• 对于线性化系统，退化因子$D$是$A$的函数，与$b$无关。这说明退化方向只与原始的约束方向$A$有关，与原始约束的位置$b$无关。这和前面的推测一致，当原始约束方向平行的时候，就会引入退化。
• 对于线性化系统，退化因子$D$的求解为$D={\lambda }_{min}+1$，其中${\lambda }_{min}$是$A^{T}A$的最小特征值。这说明$A^{T}A$的特征值和特征向量分别决定了是否存在退化以及退化的方向，对于${\lambda }_{min}={\lambda }_1$，它的退化方向就是$A^{T}A$对应于${\lambda }_{min}$的特征向量$v_{min}=v_1$

系统退化与否和系统是否存在解没有必然联系，即使系统出现退化，系统也是可能存在解的，因此需要将系统的解进行调整，一个策略就是将解进行投影，对于退化方向，使用优化的状态估计值，对于非退化方向，依然使用方程的解。另一个策略就是直接抛弃解在退化方向的分量。
因此有下面的表达式。$v_1,...,v_m$对应的特征值小于阈值，因此被视为退化的方向向量。$v_m+1,...,v_n$对应的特征值大于阈值，因此被视为非退化方向向量。
$$V_p=[v_1,...,v_m,0,...,0{]}^T$$$$V_u=[0,...,0,v_m+1,...,v_n{]}^T$$$$V_f=[v_1,...,v_m,v_m+1,...,v_n{]}^T\text{\hspace{1em}(4)}$$
对应的重投影解为，其中$x_p$为真实状态的最优预测解，$x_u$为非线性优化得到的更新解。
$$x_f=x_p^{\prime }+x_u^{\prime }$$$$x_u^{\prime }=V_f^{-1}{V}_u{x}_u$$$$x_p^{\prime }=V_f^{-1}{V}_p{x}_p\text{\hspace{1em}(5)}$$
可以这样认为，先求出$V_p{x}_p$这是最优预测解在退化方向的分量，然后逆投影到$V_f^{-1}$解空间中，可以认为$V_f{x}_p^{\prime }=V_p{x}_p$。后面的类似，就可以得到真正的优化解$x_f$
下图中蓝色表示非退化方向，橘色表示退化方向。

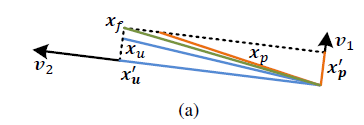
对于实际应用中，这里的应用指非线性求解，算法流程可以表示如下，对于退化方向，我们不考虑，直接丢弃，只考虑非退化方向解的增量。流程中第10行的公式有问题应该为$$x_f=x_f+V_f^{-1}{V}_u\Delta x_u\text{\hspace{1em}(6)}$$
根据经验，只需要在运行开始计算一次$V_f^{-1}{V}_u$就行。

由于退化的存在，在估计问题中，全局最小的解（橘色）不一定等于真实位姿（蓝色），因此只在非退化方向上（橘色）进行更新，最终得到优化解$x_f$（绿色），比全局最小解（橘色）更加靠近真值。

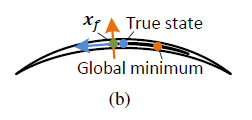
3. 参考代码

这是在LOAM中一段代码，使用了该方法。
需要求解之前的公式$(2)$
$$arg\underset{x}{\min }||Ax-b|{|}^2$$

• if (iterCount == 0)只是迭代的最开始会进行退化分析
• float eignThre[6] 判断是否退化的阈值数组
• matP = matV.inverse() * matV2的数学公式表示为$V_f^{-1}{V}_u$
• $V_f$和$V_u$中行向量均为$A^{T}A$的特征向量．

这里发现了一点错误，原始代码中使用Opecv库计算特征向量，因此V中的每一行都是特征向量

/*Calculates eigenvalues and eigenvectors of a symmetric matrix.
 bool cv::eigen 	( 	InputArray  	src,
 		OutputArray  	eigenvalues,
 		OutputArray  	eigenvectors = noArray() 
 ) 	
 The function cv::eigen calculates just eigenvalues, or eigenvalues and eigenvectors of the symmetric matrix src:
 src*eigenvectors.row(i).t() = eigenvalues.at<srcType>(i)*eigenvectors.row(i).t()*/
cv::eigen(matAtA, matE, matV);

而在Eigen中，matV的每一列都是特征向量.

    /** \brief Returns the eigenvectors of given matrix.
      *
      * \returns  A const reference to the matrix whose columns are the eigenvectors.
      *
      * \pre The eigenvectors have been computed before.
      * 
      * */
         matV = esolver.eigenvectors().real();

因此更正之后的代码如下，但是我运行时，更改前后没有太大区别，可以想一想为什么？哈哈．

            Eigen::SelfAdjointEigenSolver< Eigen::Matrix<float, 6, 6> > esolver(matAtA);
            matE = esolver.eigenvalues().real();
            matV = esolver.eigenvectors().real();
            //这里有点问题，matV中列向量是特征向量，因此需要转置．
            // matV2 = matV;
            matV2 = matV.transpose();

            isDegenerate = false;
            float eignThre[6] = { 10, 10, 10, 10, 10, 10 };
            for (int i = 0; i < 6; i++)
            {
               if (matE(0, i) < eignThre[i])
               {
                  std::cout<<"eigenThre"<<matE(0, i);
                  for (int j = 0; j < 6; j++)
                  {
                     matV2(i, j) = 0;
                  }
                  isDegenerate = true;
               }
               else
               {
                  break;
               }
            }
            // matP = matV.inverse() * matV2;
            //需要进行转置
            matP = matV.transpose().inverse() * matV2;

这是原始参考代码，有错误，上面已经指出了

      matAt = matA.transpose();
      matAtA = matAt * matA;
      matAtB = matAt * matB;
      matX = matAtA.colPivHouseholderQr().solve(matAtB);

      if (iterCount == 0)
      {
         Eigen::Matrix<float, 1, 6> matE;
         Eigen::Matrix<float, 6, 6> matV;
         Eigen::Matrix<float, 6, 6> matV2;

         Eigen::SelfAdjointEigenSolver< Eigen::Matrix<float, 6, 6> > esolver(matAtA);
         matE = esolver.eigenvalues().real();
         matV = esolver.eigenvectors().real();

         matV2 = matV;

         isDegenerate = false;
         float eignThre[6] = { 100, 100, 100, 100, 100, 100 };
         for (int i = 0; i < 6; i++)
         {
            if (matE(0, i) < eignThre[i])
            {
               for (int j = 0; j < 6; j++)
               {
                  matV2(i, j) = 0;
               }
               isDegenerate = true;
            }
            else
            {
               break;
            }
         }
         matP = matV.inverse() * matV2;
      }

      if (isDegenerate)
      {
         Eigen::Matrix<float, 6, 1> matX2(matX);
         matX = matP * matX2;
      }

4. 参考链接

• Zhang J , Kaess M , Singh S . On degeneracy of optimization-based state estimation problems.[C]// 2016 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2016.

免费原始链接On_degeneracy_of_optimization-based_state_estimation_problems
优快云1积分链接，带备注优快云_On_degeneracy_of_optimization-based_state_estimation_problems