考虑病毒传播风险的配送优化

在新冠疫情爆发期间优化生活物资配送

摘要

2019冠状病毒病（COVID‐19）疫情已在全球范围内蔓延，对人类构成了巨大威胁。居家隔离是减少物理接触及相关新冠病毒传播风险的有效方式，但需要高效的生活物资（如肉类、蔬菜、粮食和油）配送作为支撑。值得注意的是，潜在感染者的存在增加了配送过程中的新冠病毒传播风险，配送员可能成为病毒在城市居民之间传播的媒介。然而，传统配送路径优化方法并未考虑病毒传播风险。本文提出了一种新的生活物资配送路径方法，考虑了配送过程中可能发生的新冠病毒传播。构建了一个基于复杂网络的病毒传播模型，用于模拟城市居民与配送员之间的可能新冠病毒感染过程。提出了一个兼顾病毒传播风险和总路线长度的双目标模型，并采用融合自适应大邻域搜索与模拟退火的混合元启发式算法进行求解。实验在中国武汉开展，以评估所提出方法的性能。结果表明，935辆车辆将总共行驶 56,424.55公里，向3,154个社区运送必要的生活物资，总风险为 δ 40425。与传统的基于距离的优化方法相比，该方法使新冠病毒传播风险降低了67.55%。该方法有助于交通运输领域对新型冠状病毒肺炎疫情做出更有效的应对。

一、引言

HUMANS 长期以来一直受到流行病的困扰，例如黑死病、“西班牙流感”等[1]。自2000年以来，已发生多次多种冠状病毒疫情，包括严重急性呼吸综合征（2003）、中东呼吸综合征（2012）等。2019年12月，新型冠状病毒肺炎（COVID‐19）疫情暴发，并迅速蔓延至全球。截至 2020年5月23日，全球报告确诊病例达510万例，其中33万人死亡[2]。目前，新型冠状病毒肺炎对人类构成巨大威胁，严重破坏社会经济发展。限制出行和聚集是切断新型冠状病毒肺炎传播的有效手段[3]。武汉市疫情防控部门鼓励民众居家以降低感染风险。2020年1月23日，武汉实施“封城”。公共汽车、地铁、轮渡等公共交通停运，机场和火车站暂时关闭。2020年2月14日，提出小区封闭政策以加强居家隔离[4]。这一形势迫切需要紧急生活物资（如肉类、蔬菜、粮食和油）以保障居民基本家庭生活。政府与企业密切协作，收集居民需求、组织生活物资并进行配送。

生活物资配送是居家隔离的关键。约有300万名配送司机被鼓励参与生活物资的配送，以确保居家隔离顺利进行[5]。然而，新型冠状病毒肺炎可能随着生活物资配送过程传播。由于配送员频繁接触生活物资，而部分生活物资的包裹表面可能附着新型冠状病毒，因此他们面临较高的感染风险。在中国北京和大连已有多起病例报告表明，生活物资（即冷冻食品）的包裹表面可能导致新冠病毒感染[6]。此外，配送员可能接触其他人，若一名配送员被感染，他/她可能成为新型冠状病毒肺炎的超级传播者。例如，印度德里马尔维亚纳加尔的一名披萨配送男孩确诊感染新型冠状病毒肺炎，导致其配送过的72户家庭被迫隔离[7]。类似案例也在中国北京和深圳被报道[8]。因此，必要的生活物资配送将增加新型冠状病毒肺炎的传播风险。

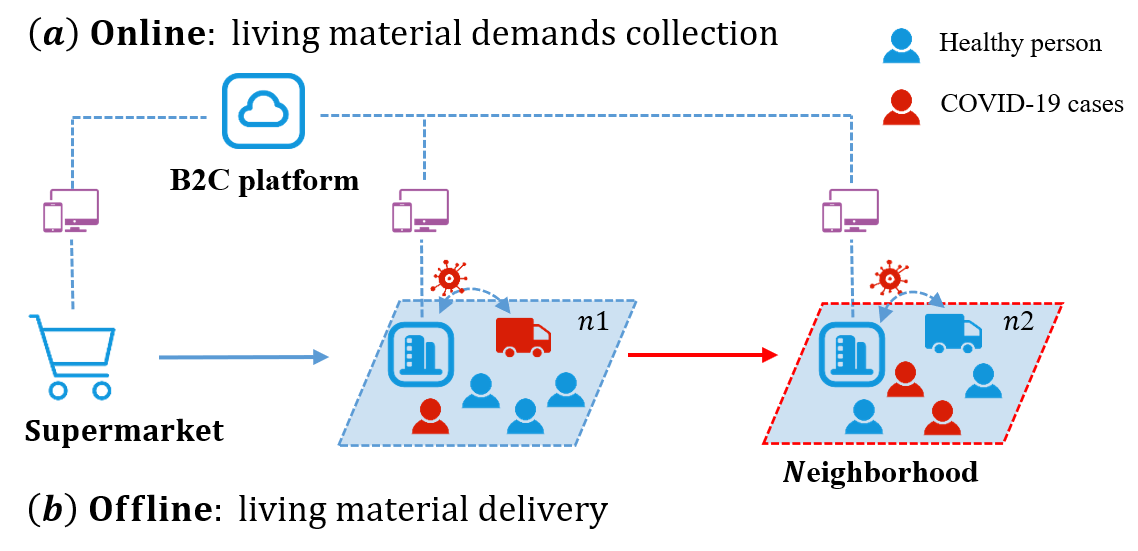
新型冠状病毒肺炎可能由于必要的生活物资配送而在社区之间传播。尽管采用快递柜等无接触配送方式可以减少配送员与城市居民之间的直接身体接触，但由于必要的人‐物‐人交互，配送过程中仍存在不可忽视的风险。图1展示了生活物资配送的生命周期。居民首先在在线B2C平台上下单购买生活物资。超市接收订单、备货，并指派配送员进行配送。在新型冠状病毒肺炎疫情初期，许多社区中存在确诊和疑似病例，但由于医疗资源有限以及病毒传播速度快，这些病例未能得到及时检测和妥善处理。因此，当配送员直接或间接接触到这些新型冠状病毒肺炎病例时，可能会将病毒带入后续配送的社区。例如，若某社区存在新型冠状病毒肺炎病例（即n1），配送员可能被感染，并将新型冠状病毒肺炎病毒带到下一个社区n2。

在配送过程中测量新型冠状病毒肺炎传播风险是前提条件。已有若干流行模型被开发用于模拟和预测病毒传播 [9]，例如易感‐感染模型（SI）、SIR模型和SEIR模型。这些模型关注病毒感染状态的转换及潜伏期，假设人与人之间的接触是同质的。但这一假设受到挑战，因为某些人的日常出行存在显著差异[10]。特别是配送员在城市中的出行最多。通常，人类移动行为可用复杂网络来刻画，该网络表示节点之间的连接与交互。基于复杂网络的病毒传播能够很好地描述基于群体的病毒扩散过程[11]。在本研究中，我们提出一个病毒传播风险指标 δ，以探究生活物资配送带来的风险。同时，开发了一种基于复杂网络的方法，用于量化不同配送方案下的新型冠状病毒肺炎传播风险。

在疫情期间优化生活物资配送路线属于应急物流领域。以往的应急物流研究主要关注应急物流网络[12]的设计或物资运输[13]的规划，以应对地震、暴雨和台风等突发事件。这些研究通常十分重视效率和不可靠性应急物流。值得注意的是，在疫情事件的配送过程中，病毒传播风险很少被考虑。

考虑到病毒传播风险，本文提出了一种新的考虑病毒传播的生活物资配送路线优化方法（DROVT），以支持必要的居家隔离。构建了基于复杂网络的病毒传播模型，用于模拟居民与配送员之间可能发生的新型冠状病毒肺炎传播。提出了一个兼顾新型冠状病毒肺炎传播风险和总路线长度的双目标模型，并采用结合自适应大邻域搜索算法 （ALNS）与模拟退火算法（SA）的混合元启发式算法进行求解。在武汉开展的实验评估了DROVT的性能。结果表明，所提出的方法在病毒传播防控与生活物资配送效率之间实现了良好的平衡。具体而言，本研究的主要贡献总结如下：
- 基于复杂网络的病毒传播动力学模型被提出，用于评估配送员和社区的新型冠状病毒肺炎传播风险。
- 一种考虑病毒传播和配送效率的配送路线优化框架被提出。
- 一种融合自适应大邻域搜索算法和模拟退火算法的混合元启发式方法被提出，以寻找高质量的生活物资配送方案。
- 一组实验在武汉设计，用于验证提出的方法的有效性。探讨了车辆容量、出行管控和个人防护等多个因素的影响。

本文其余部分组织如下。第二节回顾了相关文献。第三节介绍了研究区域和数据集。第四节描述了提出的方法。第五节报告了实验和结果。最后一节第六节总结了本研究。

II. 相关工作

A. 疫情传播模型

疫情传播建模旨在分析和预测疾病传播过程及模式 [13]。最典型的疫情传播模型是仓室模型SIR，该模型最初被用于研究黑死病大流行的传播[14]。SIR模型通常假设人口被划分为若干仓室，例如易感者（S）、感染者（I）和康复者（R）。根据疾病特征（即基本再生数R0）来模拟和预测疾病的演变。基于SIR原理，已发展出多种模型，包括SEIR、SIQR和SEIQR[15]。需要注意的是，这些模型假设个体在空间上是同质的，忽略了现实世界疫情传播过程中复杂的空间和拓扑结构，尤其是在高密度城市中。

人群之间的接触呈现出一些复杂网络特征，例如小世界、无标度等[11],[16]。基于复杂网络的模型已经被提出用于模拟和预测疫情传播。通常，基于复杂网络的传染病传播模型可分为两类：（1）基于个体接触的网络模型（ICNM），其中节点代表个体，边代表个体之间的物理接触。通过沿着边传播，病毒会感染健康个体并在人群中扩散。例如，zhang et al.[15]基于社会接触网络改进了SIR模型，在社会接触网络上模拟病毒暴发，并提出了一些免疫策略。（2）元群体网络模型（MNM），其中节点表示一组人群，边表示组间接触[17]。MNM在群体层面而非个体层面进行模拟和预测，因此适用于模拟疫情从一个地理区域向另一个地理区域的传播。例如，Calvetti et al.[18]构建复杂网络，通过将节点特征化为接触频率以及与其他节点的连通性，来预测美国密歇根州和俄亥俄州的新型冠状病毒肺炎疫情。遵循MNM方法，我们将社区视为元群体，模拟新型冠状病毒肺炎在社区之间的传播以及与配送过程的关联。考虑病毒传播的DROVT方法被开发出来，以提供高效的生活物资配送，支持必要的居家隔离。

B. 应急物流

应急物流是指在疫情、暴雨和台风等事件期间提供必要人道主义服务的专门运输活动[19],[20]。应急物流通过提供必要的日常生活物资（即水、食物和药品）来强调人道主义救援。以往关于应急物流的研究可分为三类：（1）选址应急物流设施以提供有效的应急服务，例如为震后救援定位应急物资供应中心以及选址急救救护车站点 [21],[22]；（2）设计应急物流网络以提高响应效率或增强物流可靠性[23],[24]；（3）优化应急配送，在考虑不确定的道路交通或有限的物资供应的情况下设计最优配送路线[25],[26]。这些应急物流任务具有较高的计算复杂度，因此难以找到最优解。为此开发了启发式算法，以在合理时间内获得高质量解。元启发式算法包括智能搜索（如遗传算法（GA）[24],、蚁群优化（ACO）[27],等）和局部搜索，（即大规模邻域搜索（LNS）[28], SA、禁忌搜索（TS） 等[29]–[31],被提出，通过保持解搜索过程中强化与多样化之间的平衡[32]来寻找近似最优解。特别是，ALNS元启发式算法扩展了LNS框架，通过破坏当前解并修复它，以迭代探索邻域解。自适应大邻域搜索算法在车辆路径问题（VRP）和调度问题[33],[34]中已取得成功。

疫情应急物流也引起了一些关注。例如，Zaric和 Brandeau [35]采用成本效益分析方法研究了疫情防控中医疗资源的分配问题。最近，一些研究探讨了应急医疗物流服务的优化。Dasaklis et al.[12]提出了一个应急物资配送网络优化模型，以提供大规模疫苗接种服务来应对天花疫情爆发。在生活物资配送方面，Ekici et al. [13]对流感大流行进行了建模，并使用启发式算法规划食物配送。这些研究为应对医疗紧急情况提供了有益的见解。然而，由于流行病期间配送活动带来的病毒传播风险常常被忽视。为弥补这一空白，本研究开发了DROVT方法，在考虑病毒传播的同时优化生活物资配送。本文提出了一种融合自适应大邻域搜索算法（ALNS）和模拟退火算法（SA）的混合元启发式方法，以求得高质量解。

III. 研究区域与数据

本研究在中国武汉进行，武汉总面积为8,569.15km²，人口为1420万[36]。该市共有13个行政区，其中7个为核心城区，即江岸、江汉、硚口、汉阳、青山、武昌和洪山。2019年12月，武汉报告了数例不明原因肺炎病例。在接下来的一个月里，武汉成为中国新冠疫情暴发的疫情中心。在新冠疫情暴发期间，约有500万人口离开武汉，而大约 900万人口留在市区内[37]。

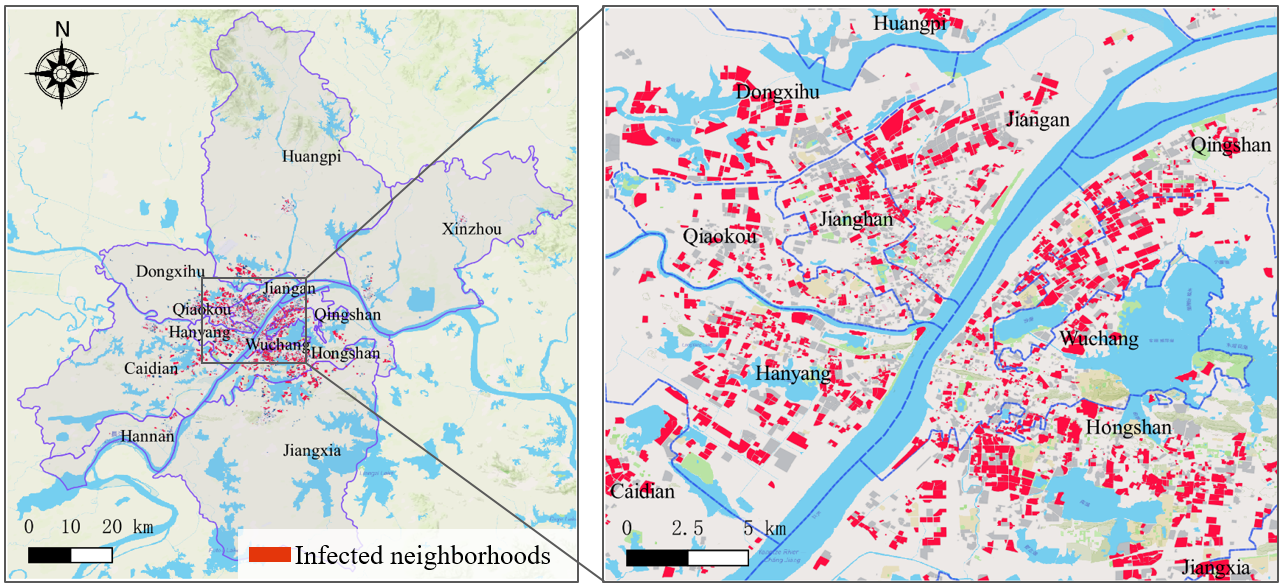
新冠肺炎病例数据集收集了2020年2月3日至3月3日武汉市核心城区的数据。其中包括表I所报告的确诊和疑似新冠肺炎病例数量。共收集了3,154个社区，其中2,349个社区报告了确诊或疑似病例。关于生活物资供应支持，现有 26个配送中心、526个物资供应超市和935辆车。道路网络数据来自开放街图（OSM）。车辆平均速度设置为40 km/h。

表I 居民小区新型冠状病毒肺炎数据

行政区	社区数量	确诊病例数	疑似病例数
江岸	378	1234	321
江汉	412	1567	432
硚口	395	1345	389
汉阳	367	1423	401
青山	354	1123	312
武昌	402	1356	378
洪山	446	1489	421

图2显示了社区层级报告的新冠肺炎病例的空间分布。可以看出，江汉、汉阳和洪山的一些社区感染较为严重，而黄陂和新洲等郊区地区的感染病例较少。这也表明，新冠肺炎病例从核心城区向郊区逐渐减少。

为支持居家隔离，政府、企业和社区合作提供生活服务。选取超市武商良范、中百超市、沃尔玛和家乐福作为供应中心。为估算日常生活物资需求，我们收集了住宅总建筑面积以估算人口。通常情况下，根据中国居民膳食指南（CDG）[38],，考虑三类基本生活物资，包括蔬菜、肉类和粮食。如表II所示，其数量也根据中国居民膳食指南（CDG）的建议设定。

表II 一个人的基本日常生活物资需求

物资类别	日均需求量
蔬菜	0.5 kg
肉类	0.2 kg
粮食	0.4 kg

IV. 方法论

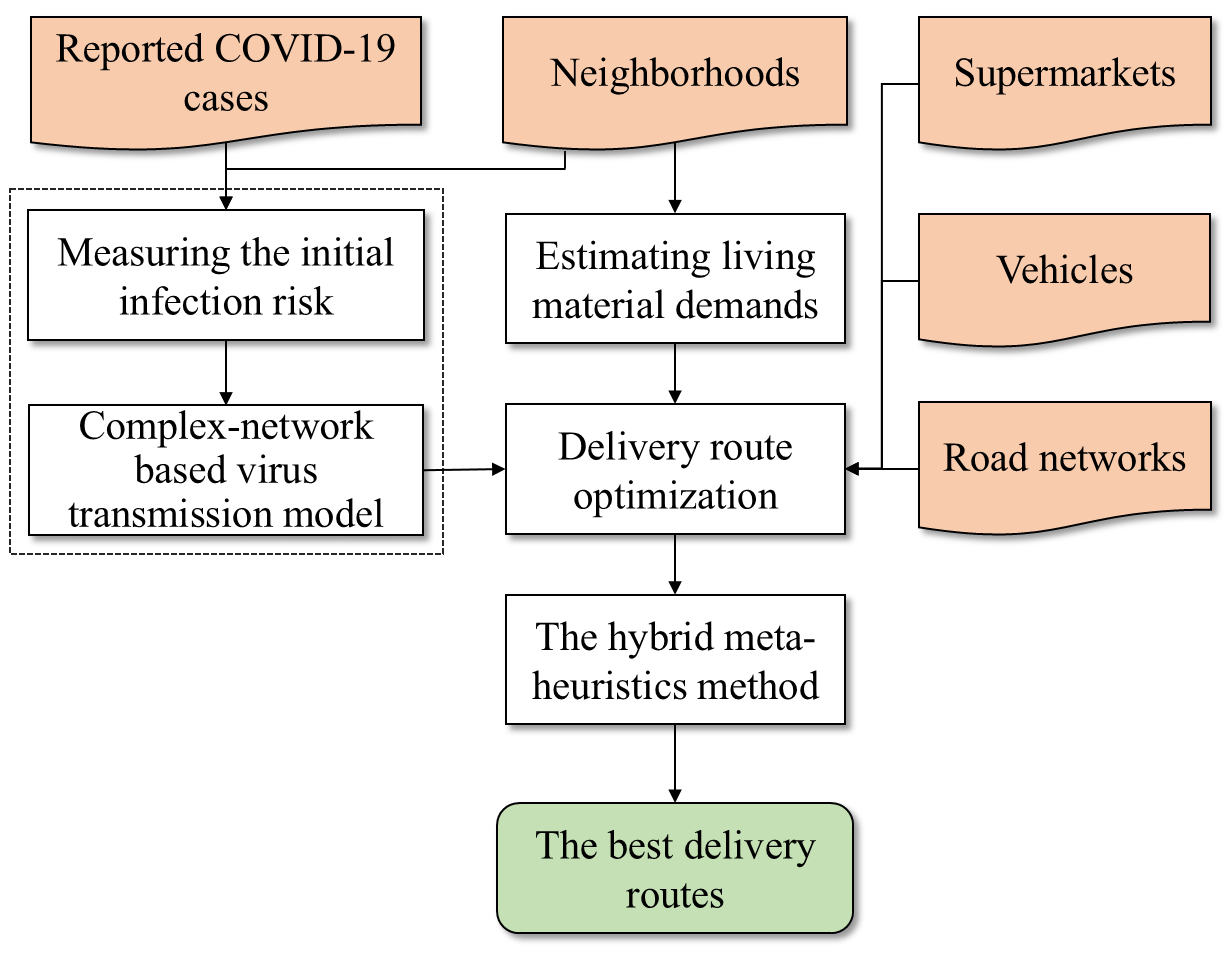
我们开发了DROVT方法，以在新型冠状病毒肺炎威胁下提供有效且高效的生活物资配送服务。DROVT的框架如图3所示。首先，估计每日生活物资需求；然后，利用基于复杂网络的病毒传播模型测量配送过程中的病毒传播风险；最后，建立并求解一个考虑病毒传播风险的配送路径优化模型，该模型采用结合自适应大邻域搜索算法和模拟退火算法的混合元启发式算法进行求解。框架的详细内容如下所述。

A. 估算日常生活物资需求

我们根据住宅总建筑面积数据估算日常生活物资需求。人口是根据武汉的人均居住面积（PC L S），PCLS= 35(m²/person)计算得出的。每住户单元的人口根据家庭结构设定。一个社区Ni的日常生活物资总需求等于各家庭数量（Hb）与其日常生活每人所需的生活物资需求量（∑₃ l=1 ql），如公式(1)所示，其中l表示一种生活物资，b表示一栋建筑，i表示一个社区。

$$ N_i = \sum_{b \in n} H_b \times \sum_{l=1}^{3} q_l $$ (1)

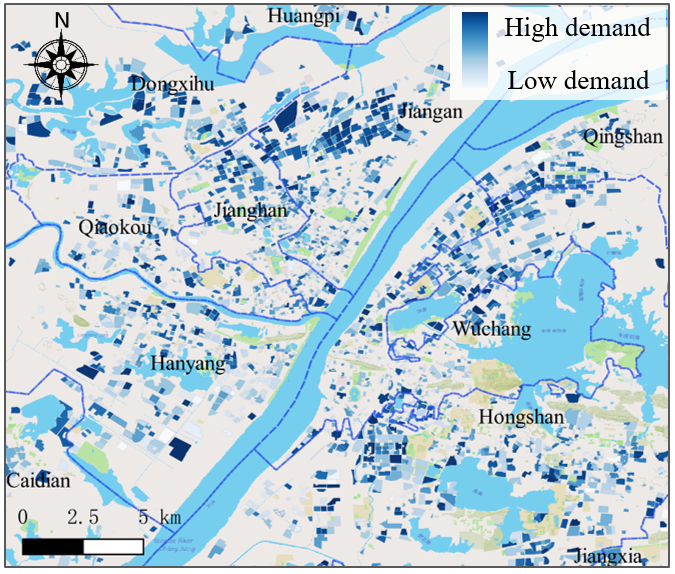
经过数据处理，武汉每天需要8,601.55吨生活物资，其中包括蔬菜3,693.92吨、肉类1,319.26吨以及粮食和油类3,588.38吨。图4展示了每日生活物资需求的空间分布。结果显示，各社区的生活物资需求量在0.01至12.2吨之间。通过将每个社区分配给最近的超市，必要生活物资配送将建模如下。

B. 基于复杂网络的病毒传播模型

基本生活物资配送服务可能导致人与人之间的病毒传播。复杂网络能够模拟人群的群体划分和交互，因此可以很好地描述疫情传播过程。它涉及疫情暴发阈值的设定以及感染者随时间的演化特征。一个复杂网络包含两个要素：节点和边。对于生活物资配送过程而言，节点代表社区、超市或配送中心，边代表社区、超市或配送中心之间的出行。

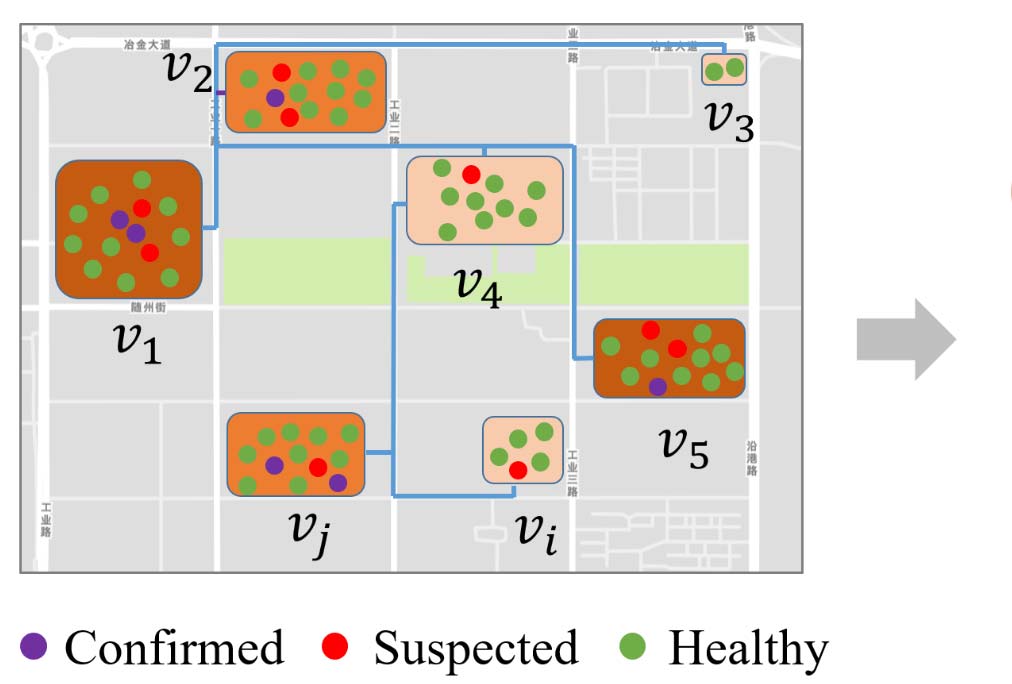
MNM用于描述由于生活物资配送导致的社区间新型冠状病毒肺炎传播的动态过程，如图5所示。通常，一个社区i包含一组人群，其中有一些确诊和疑似新型冠状病毒肺炎病例。考虑到这些新冠病例不同的传播能力，我们为其设定不同的病毒传播风险。因此，一个社区可以用初始新型冠状病毒肺炎概率ri来描述，如公式(2)所示，其中Pic, Pis分别表示确诊和疑似新型冠状病毒肺炎病例的数量，ε₀和 ε₁分别为这两类病例相应的传播概率。根据Yang等人[39], 的研究，这两个值分别设为1和0.15。通过对社区的概率进行归一化处理，我们将社区内的新型冠状病毒感染风险βi统一表示为公式(3)，其中rmin和rmax分别为城市中所有社区的最小和最大风险值。如图5所示，新型冠状病毒肺炎病例越多， βi的值越大。

$$ r_i = \varepsilon_0 \times P^c_i + \varepsilon_1 \times P^s_i $$ (2)

$$ \beta_i = \frac{r_i - r_{min}}{r_{max} - r_{min}} $$ (3)

当配送员在城市中出行时，由于人与人或人与物的必要接触，导致了新型冠状病毒肺炎的传播。通常，从超市到社区的生活物资配送可以用有向图G(V,E)来描述，其中 V≡{v1, v2,…vn}表示所有节点的集合，E ≡{e12, e23,… eij},(i,j ∈ V)表示所有边的集合。在本研究中，节点表示社区、超市和配送中心，边表示从一个社区到另一个社区的出行路线段。

病毒在配送过程中存在两种传播情况。一种情况是，当配送员分发生活物资时，新型冠状病毒肺炎可能在社区居民与配送员之间传播，具体取决于接触情况和病毒防护水平。此处，用 θi表示配送过程中的病毒传播风险，其反映了配送过程中的接触方式。θi的取值范围在0到1之间。形式上，单次配送操作的传播概率可按公式(4)计算，其中di表示社区i的防护水平， Δt表示配送员在社区i停留的时间，由装卸时间决定。装卸操作时间越长，包裹、配送员与居民之间的接触越多，病毒传播概率pi就越高。在本研究中，我们设定假设采用接触递送，将 θi的值设为1，因为我们不了解配送中的接触或非接触情况。

$$ p_i = (1 - \exp(-d_i \times \Delta t)) \times \theta_i $$ (4)

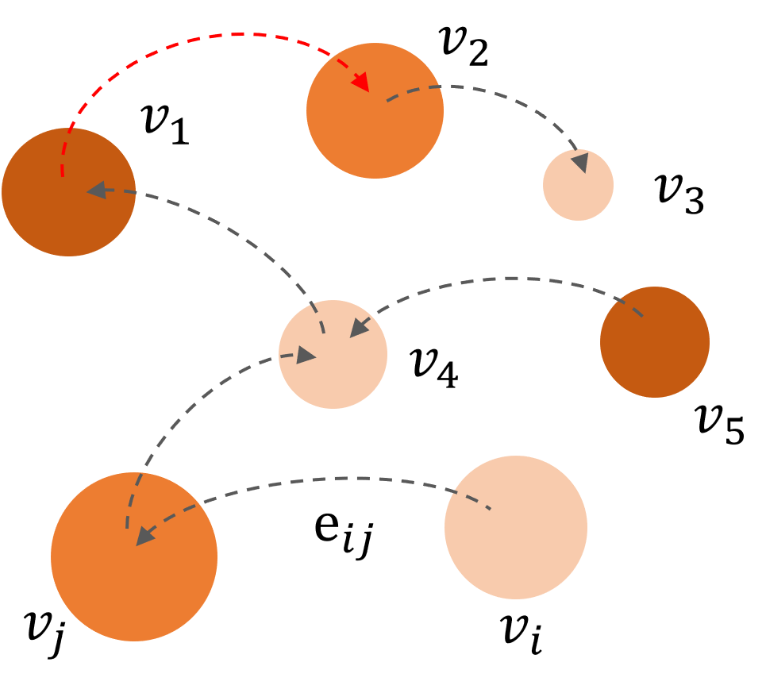
另一种情况是病毒可能从配送员传播给居民。通常情况下，配送员服务的社区越多，病毒传播风险就越高。因此，病毒传播风险应沿配送员的路线累积，如图6所示。在一次配送操作后，社区的感染风险 βi+等于配送前的风险βi−加上本次配送带来的新增风险 γhi×pi，如公式(5)所示。对于配送员而言，一次配送操作后的病毒传播风险γij等于之前的风险加上所访问节点的风险，如公式(6)所示，其中γhi和γij分别为边ehi和边eij的风险，h是此前访问过的社区。配送网络风险最终由一个指标 δ表示，如公式(7)所示，该指标等于所有社区的累积风险以及配送完成后配送员的累积风险。所有配送完成的时间用T表示。

$$ \beta_i^+ = \beta_i^- + \gamma_{hi} \times p_i $$ (5)

$$ \gamma_{ij} = \gamma_{hi} + \beta_i^- \times p_i $$ (6)

$$ \delta = \sum_{i \in V} \beta_i^+(T) + \sum_{i \in V} \sum_{j \in V, j \neq i} \gamma_{ij} $$ (7)

C. 考虑新冠肺炎传播的配送路径优化模型

由于新型冠状病毒肺炎可能在生活物资配送过程中传播，我们提出了以下配送路线优化问题(DROP)。该问题的目标是降低因必要生活物资配送带来的病毒传播风险。此处，我们假设充足的物流车辆将被部署在配送中心。各社区的生活物资订单被分配至最近的超市。一辆车辆从配送中心出发，在超市装载生活物资后，将其配送至对应的社区，然后返回出发的配送中心。车辆在城市中行驶以完成生活物资包裹的配送，直到所有社区的订单均被送达。

形式上，所建立的配送路线优化问题(DROP)表述如下：首先给出四个集合和三个约束条件。
(1) 配送中心集合为 D ≡{d1, d2,…dh}，(2) 车辆集合为 H ≡{H1, H2,… Hd}，(3) 超市集合为 M ≡{m1, m2,…me}，(4) 社区需求订单集合 C 为 C ≡{c1, c2,… ci}。
(5) 所有车辆从各自的配送中心出发，最终返回配送中心， (6) 车辆的载重量不得超过其载重容量MQ，(7) 配送员的工作时长不超过规定的工作时长MT。

配送路线优化问题（DROP）可以表示为一个有向图 G(V,E)。图中的节点集合V ≡{D, M,C}由车辆的配送中心、超市和社区组成。边集合E表示从一个节点出发的路线段到另一个。每条边 eij 表示从节点i到节点 j的一条路线段，出行距离为dij。路线优化问题（DROP）包含两个组成部分：新型冠状病毒肺炎传播风险和出行距离。此处，总传播风险包括所有社区的风险以及所有配送员的风险。通常情况下，从一个超市直接向一个社区配送将产生最小的病毒传播风险，因为不存在社区之间的间接病毒传播。然而，这需要数千辆车辆和配送员，导致更多配送员暴露于新型冠状病毒肺炎风险中。因此，应协调这两个目标函数。在此，通过使用权重参数α，我们将配送路线优化问题（DROP）转化为单目标问题。形式上，本文提出了一种混合整数规划模型来描述该配送路线优化问题（DROP）。

决策变量 :
- $x_{ij}^{dk} \in (0, 1)$：当从配送中心k出发的车辆从节点i行驶至节点j时，该二进制变量等于1；
- $T_i^{dk}$：从配送中心k出发的车辆到达节点i的时间；
- $Q_i^{dk}$：从配送中心k出发的车辆在离开节点i时的载货量；
- $\beta_i^+(T)$、$\beta_i^-(T)$：分别表示节点i在时间T之后和之前的时间段内的病毒传播风险；
- $\gamma_{ij}^{dk}$：从配送中心 k出发的车辆从节点i行驶至节点j过程中的病毒传播风险。

目标函数 :

$$
\text{Min } F = \alpha \times \left( \sum_{i \in V} \beta_i^+(T_i) + \sum_{d \in D} \sum_{k \in H_d} \sum_{i \in V} \sum_{j \in D} \gamma_{ij}^{dk} \right) + (1 - \alpha) \times \sum_{d \in D} \sum_{k \in H_d} \sum_{i \in V} \sum_{j \in V, i \neq j} d_{ij} \times x_{ij}^{dk}
$$
(8)

约束条件 :
$$
\beta_i^+(T_i^{dk}) = \beta_i^-(T_i^{dk}) + x_{hi}^{dk} \times \gamma_{hi}^{dk} \times p_i, \quad \forall d \in D, k \in H_d
$$
(9)

$$
\gamma_{ij}^{dk} = \gamma_{hi}^{dk} \times x_{hi}^{dk} + \beta_i^+(T_i^{dk}) \times p_i \times x_{hi}^{dk}, \quad \forall i,j \in V, d \in D, k \in H_d
$$
(10)

$$
\sum_{d \in D} \sum_{k \in H_d} \sum_{j \in V} x_{ji}^{dk} = \sum_{d \in D} \sum_{k \in H_d} \sum_{j \in V} x_{ij}^{dk}, \quad \forall i \in V
$$
(11)

$$
\sum_{i \in D} \sum_{j \in M} x_{ij}^{dk} < |H_d|, \quad \forall d \in D, k \in H_d
$$
(12)

$$
\sum_{j \in V} x_{dj}^{dk} = \sum_{i \in V} x_{id}^{dk} = 1, \quad \forall d \in D, k \in H_d
$$
(13)

$$
Q_i^{dk} \leq MQ \leftarrow \sum_{j \in V} x_{ij}^{dk} = 1, \quad \forall i \in V, d \in D, k \in H_d
$$
(14)

$$
T_j^{dk} = T_i^{dk} + t_{ij} + s_i \leftarrow x_{ij}^{dk} = 1, \quad \forall i,j \in V, d \in D, k \in H_d
$$
(15)

$$
T_i^{dk} \leq MT, \quad \forall d \in D, k \in H_d, i \in V
$$
(16)

$$
T_i = \text{MAX}(T_i^{dk}), \quad \forall i \in V
$$
(17)

公式(8)的第一部分表示总病毒传播风险，包括所有社区和所有配送员的累积风险。公式(8)的第二部分表示所有配送路线的总长度。 α和 1−α是两个目标函数的相应权重。公式(9)和(10)表明，在一次生活物资配送操作后，社区风险和配送员风险会被更新。公式(11)指出，在社区i的到达车辆数等于离开车辆数。公式(12)要求从一个配送中心出发的车辆数小于该配送中心所拥有的车辆数，|Hd|。公式(13)规定一辆车必须返回出发的配送中心。(14)确保一辆车累计配送的生活物资不超过其车辆容量，MQ。公式(15)指出，车辆到达节点j的时间等于其到达前一节点i的时间加上在节点i的服务时间以及从节点i行驶到节点j的行驶时间。公式(16)限制每位配送员的总工作时间必须小于规定最大作业时间，MT。公式(17)表示生活物资配送过程在节点i结束的时间$T_i^{dk}$等于最后一辆配送车辆的到达时间。

D. 混合元启发式算法

所提出的配送路线优化问题（DROP）是多配送中心车辆路径问题的一种变体[40],，因此属于NP难问题。当涉及数千个节点时，在合理时间内获得全局最优解非常困难。为此，我们开发了一种结合自适应大邻域搜索算法（ALNS）和模拟退火算法（SA）的混合元启发式算法来解决该问题。该混合元启发式算法包含两个步骤： （1）构造一个良好的初始解；（2）通过自适应大邻域搜索算法 （ALNS）和模拟退火算法（SA）对当前解进行迭代优化。

1) 初始解

初始解生成方法通过迭代将生活物资订单插入路线。工作流程如算法1所示。首先，为H中的所有车辆生成从配送中心出发的空路线（第1行）。然后，随机选择一个订单ci，并选择一条配送路线rd来插入该订单。在路线rd中，最佳插入位置(i,j)是插入成本最小的位置 （第3‐9行）。重复此插入过程，直到所有订单都被插入。

算法1 构造初始解
输入： H：车辆集合H；C：社区需求订单集合C
输出： 初始解 S
1: R ≡{r1, r2,… rd}←为车辆集合H中的h初始化路线
2: 对于所有 ci ∈社区需求订单集合C 执行
3: f_min ← ∞
4: 对于所有rd ∈路线集合R 执行
5: 如果 f_min > insert_成本 (i, j) 且 qd + qj < Qd 则
6: best_insert = (rd, i, j)
7: f_min = insert_成本 (i, j)
8: 结束 if
9: 结束 for
10: 插入_顺序 (rd, i, j)， qd += qj
11: 结束 for

2) 自适应大邻域搜索算法

自适应大邻域搜索算法 （ALNS）最初由皮辛格和罗普克（2006）提出，用于求解车辆路径问题[41]。ALNS的核心思想是通过迭代破坏和修复当前解，以寻找高质量解。算法2展示了用于改进生活物资配送方案的LNS框架。首先，初始化参数、当前解和最优解（第1行）。随机选择一个破坏算子，从当前解S中移除一组节点，然后将其重新插入以获得新解S（第2至5行）。新解将根据模拟退火准则被接受。根据破坏算子的表现，动态调整其权重（第7至12行）。移除‐插入迭代将持续进行，直到达到最大迭代次数。最后，输出所找到的最优解。

算法2 ALNS
输入：M超市 set; C社区 set; Max_Iter最大迭代次数；S初始解。
输出： 最优解 S
1：初始化参数，设置 S =S
2: 对于 k= 1到 Max_Iter do
3:选择一个破坏算子 Oi
4:通过 Q节点从 S中移除 Oi
5:通过修复算子重新插入 Q节点，生成一个新的解 S ,
6:接受当前解 S ，依据 模拟退火
7:如果 如果接受 S则
8: S=S
9:如果 f(S)<f(S ) 那么
10: S =S
11:结束如果
12:更新破坏算子 πi的权重
13:结束如果
14:结束循环

a) 破坏算子

破坏算子会从当前的配送路线中移除一组节点（即社区、超市），以扰动当前解。在本研究中，设计了四种破坏算子。将通过轮盘策略随机选择一种破坏算子。
- 随机移除（RR） ：Q 节点从当前解中随机移除。
- 高风险移除（HRR） ：风险最高的前Q−个节点将被移除。该算子会剔除构成具有较高病毒传播风险值边的节点。
- 最长路线段移除（LR） ：两个节点之间过长的配送出行可能导致不合理的配送；因此，当前解中最长路线段所连接的节点将被从当前解中移除。
- 聚类移除（CR） ：当破坏操作移除一组差异较大的节点时，这些节点可能会被重新插入到相同的位置。此处，对所有社区应用K‐均值聚类。将从解中移除一个社区聚类。K的值设置为 |C|/Q。

b) 修复算子

修复算子将被剔除的Q个节点重新插入配送路线中，以生成一个新的可行配送方案，且不违反车辆容量和工作时间约束。本质上，修复算子使用插入启发式来修复解。插入顺序会影响重新插入解的质量。根据 Tu et al.[30],的方法，我们对被移除的节点进行随机排序，并将其重新插入到合适的位置。为了避免一些较差的修复操作，我们重复执行排序‐重新插入操作Q次并评估其性能。最终采用性能最佳的重新插入结果。

c) 自适应加权策略

在一次破坏和修复操作后，某个破坏算子的权重πi将根据获得的新解进行更新，如公式（18）所示，其中πi表示一次迭代后的权重，ρ(0< ρ<1)是控制权重变化速度的参数。 ωi表示该算子 Oi在本次迭代中获得的改进成本。因此，性能越优的算子将被更频繁地使用。

$$
\pi_i = \rho \times \pi_i + (1 - \rho) \times \omega_i
$$
(18)

3) 模拟退火算法

模拟退火算法用于接受新解。采用模拟退火准则，通过Metropolis准则[42]可能接受较差的解。这能有效逃离局部最优，并增加搜索深度以生成更优解。

E. DROVT原型系统

开发了一个在线DROVT原型系统，以提供高效的生活物资配送服务。开发了一个微信小程序来收集居民的生活物资订单，如图7(a)所示。该小程序可通过广泛使用的微信轻松开发和在居民间分享。所提出的DROVT模型及求解的混合元启发式算法已在云服务器上实现并部署。图 7(c)显示了一天内的配送路线。这些路线将被发送给司机，用于路线导航和装卸操作，如图7(b)所示。

V. 实验与结果分析

实验在武汉进行。该方法在配备Intel Core i5‐3470 @3.2 GHz处理器、16 GB内存和64位Windows 10操作系统的PC上使用Python实现。为了评估提出的方法的性能，我们比较了传统ALNS方法与混合ALNS + SA元启发式方法的结果。此外，我们分析了不同车辆容量、交通管制和个人防护条件下的生活物资配送策略。

车辆容量MQ设置为3吨。最大工作时间MT设置为8小时。混合元启发式算法中有多个参数需要设定。经过预实验，我们将总行驶距离目标乘以0.01，使其数值与总病毒传播风险目标相匹配。我们设置 α为0.5，以使两个目标函数具有相等的权重。根据Tu等[33],的方法，SA的初始温度T0,设为初始解的目标函数值。冷却系数设置为 0.95。关于ALNS中移除节点的数量Q，我们将其设置为 √|D| + |C| 。ALNS中的权重更新速度控制参数ρ设置为 0.5。

A. 所提出方法的结果

在武汉数据集中，使用混合元启发式算法和自适应大邻域搜索算法求解DROVT模型。报告了目标函数、总风险、总距离和计算时间。ALNS与混合元启发式算法之间的差距评估为Gap=(H −Best)/Best，其中H表示混合元启发式算法解的目标函数值。结果如表III所示。

结果表明，935辆车将总共行驶56,424.55公里，向 3,154个社区配送必要的生活物资，总病毒传播风险为 δ 404。所得到的配送方案平衡了病毒传播风险和行驶成本。图8展示了一个解的三个指标。它表明病毒传播风险在不同社区之间存在差异。中位风险

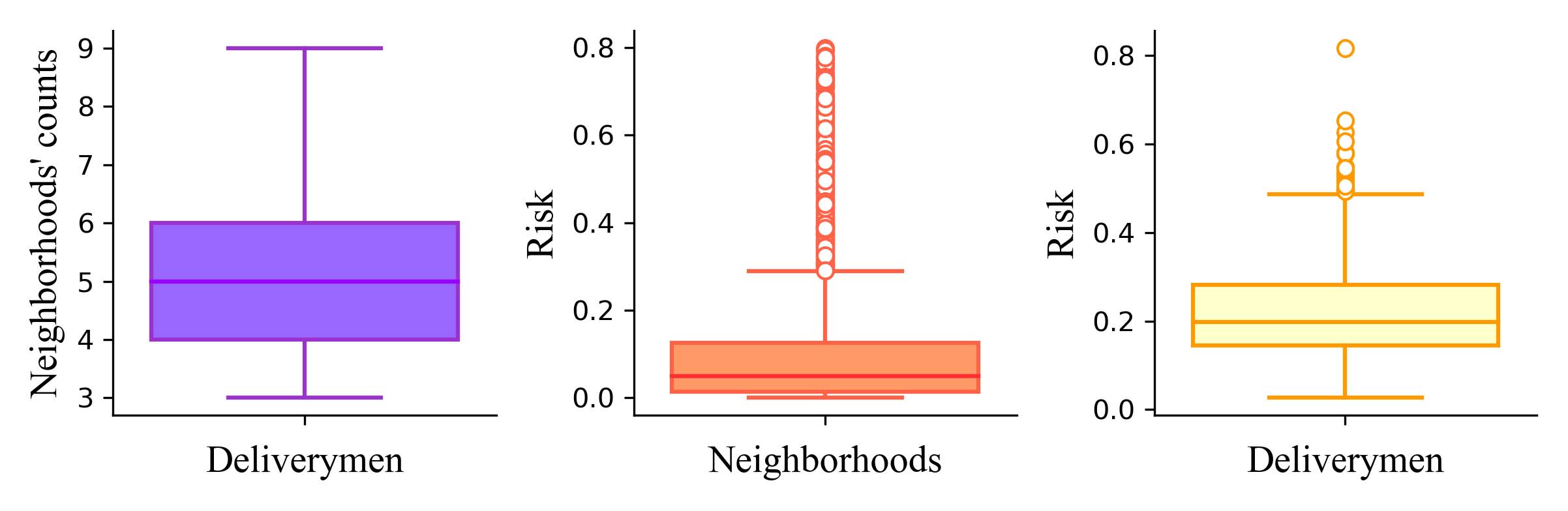
所有社区的风险值为0.05。90%的社区风险值低于0.26。配送员的中位风险为0.19。90%的配送员风险值低于 0.37。图9显示了在武汉市中心城区通过混合元启发式算法求解的配送路线，以及每条路线段上的病毒传播风险。颜色越深，风险值越大。这验证了病毒传播风险沿配送路线逐渐增加。

如表III所述，混合元启发式算法的结果优于自适应大邻域搜索算法的结果。在总风险方面，混合元启发式算法的结果（ 404.25）比自适应大邻域搜索算法的解（407.28）降低了0.75 %。在总行驶距离方面，混合元启发式算法的结果（ 56,424.55）优于自适应大邻域搜索算法的结果（58,923.14）。但混合元启发式算法也带来了更多的计算开销，仅增加了5.02%。

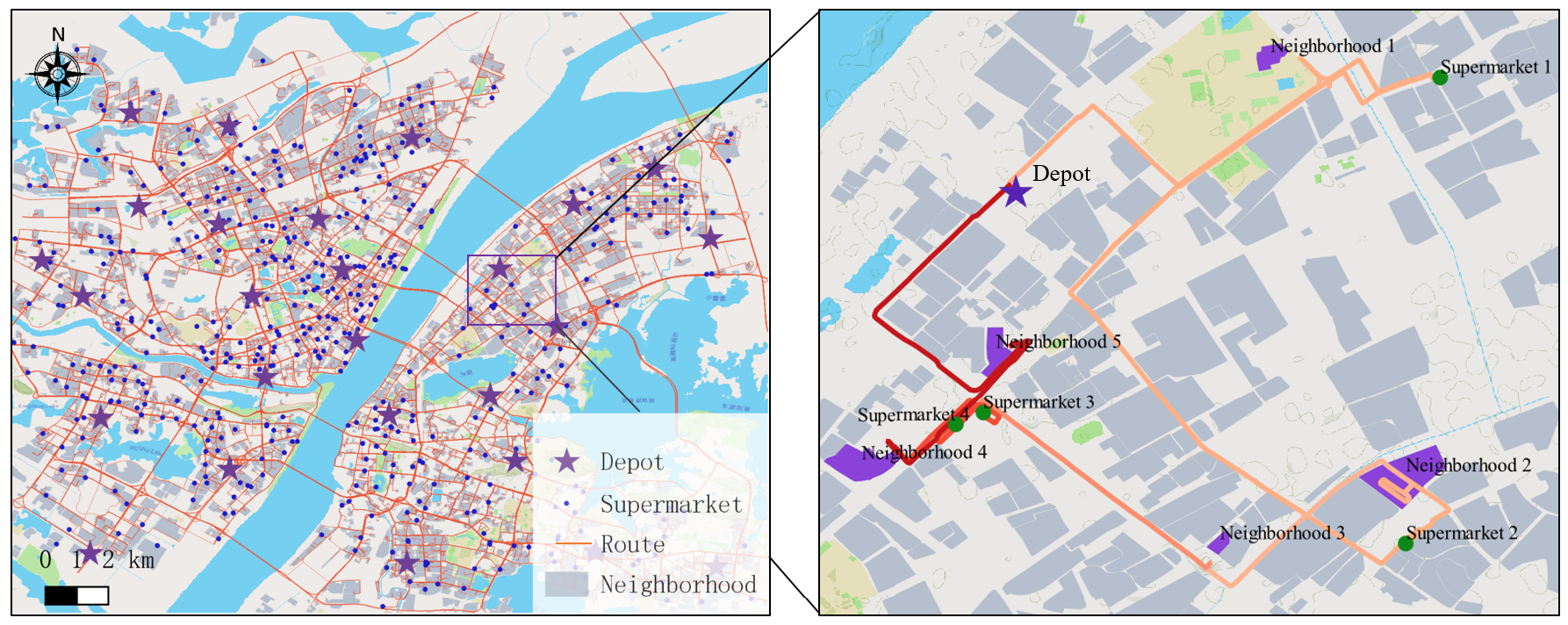
图10显示了四种破坏算子的权重变化，包括RR、 HRR、LR和CR算子。在自适应大邻域搜索算法（ALNS）的初始阶段，所有算子的权重相同，均为0.25。随着 HRR算子在目标函数上的改进效果更显著，其权重增加，而其他三个算子的权重则相应减少。最终，HRR算子的权重达到约0.6。这种权重的变化体现了所提出的HRR算子的良好性能。

B. 与基于距离的递送路由优化的比较

所提出的DROVT方法的有效性通过与基于距离的配送进行比较进一步评估

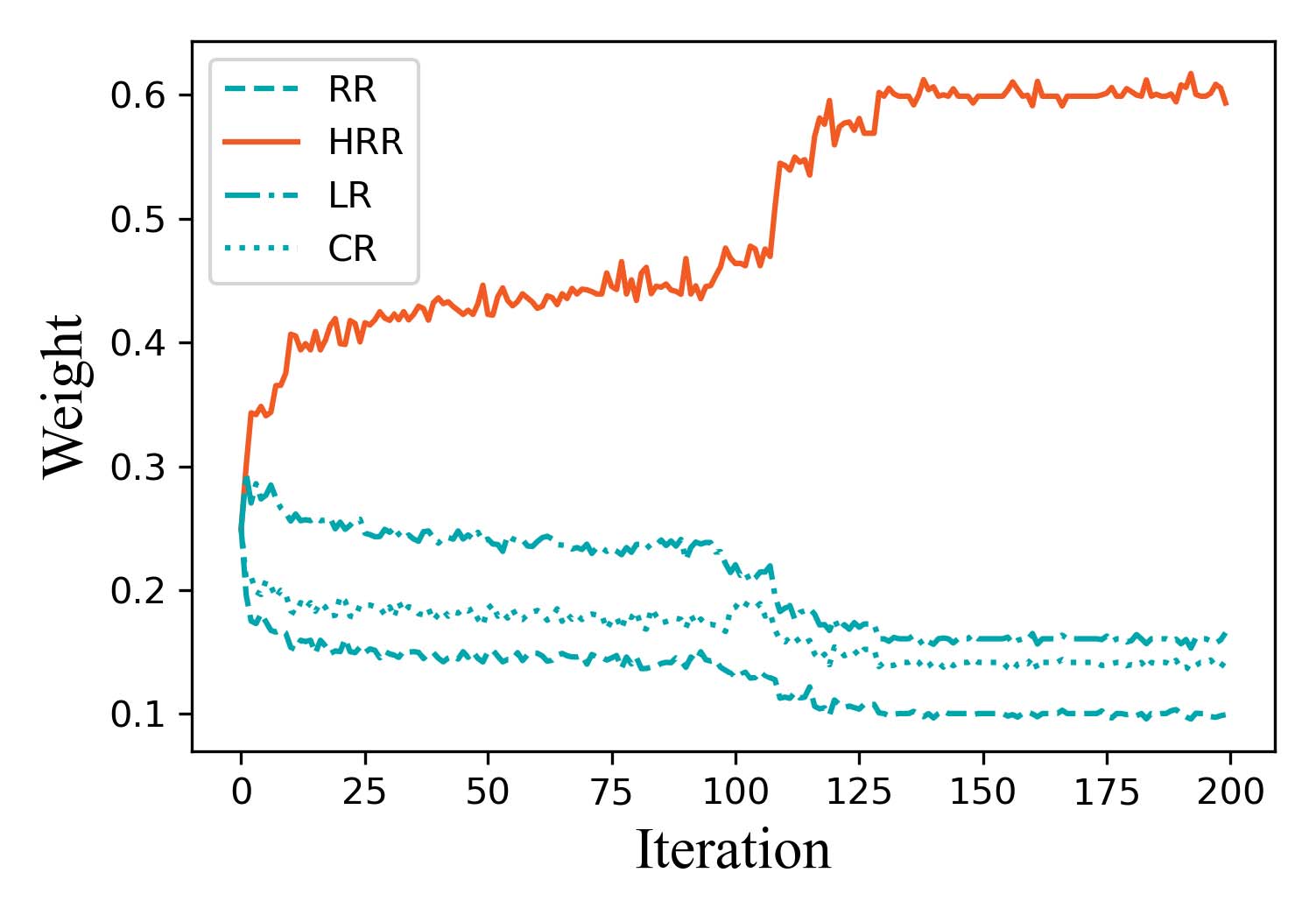
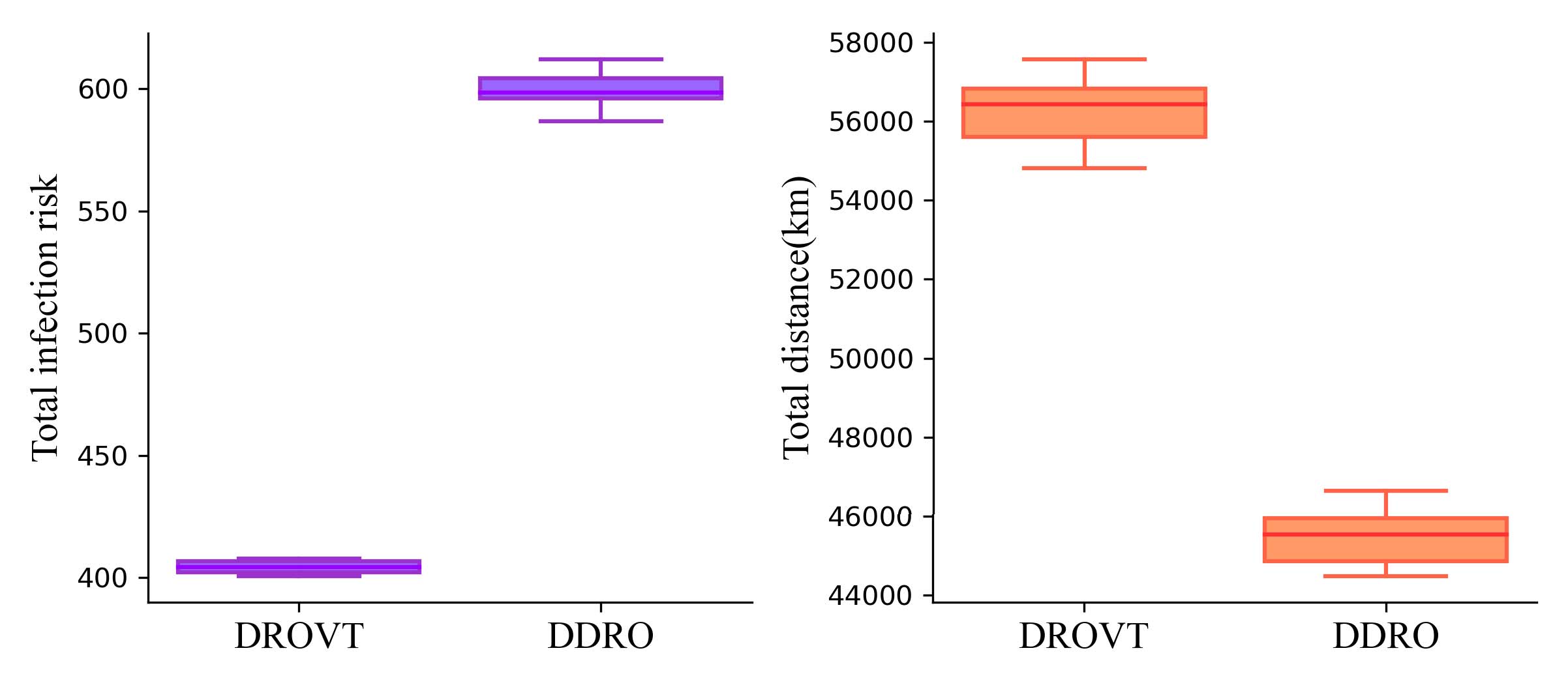
动态路由优化（DDRO）未考虑生活物资配送过程中的病毒传播，即参数 α设为0.0。我们对这些方法各运行30次，并比较所得结果。结果分布如图11所示。结果显示， DDRO的总风险 δ中位数为598.39。当考虑病毒传播时， DROVT的结果使新型冠状病毒肺炎传播风险 δ降低至 404.24，约为DDRO结果的67.5%。在总距离方面， DDRO结果的中位数总距离为45,543.02千米，低于 DROVT结果的56,424.55公里。该结果表明，DROVT通过合理绕行，在增加出行距离的同时降低了病毒传播风险。

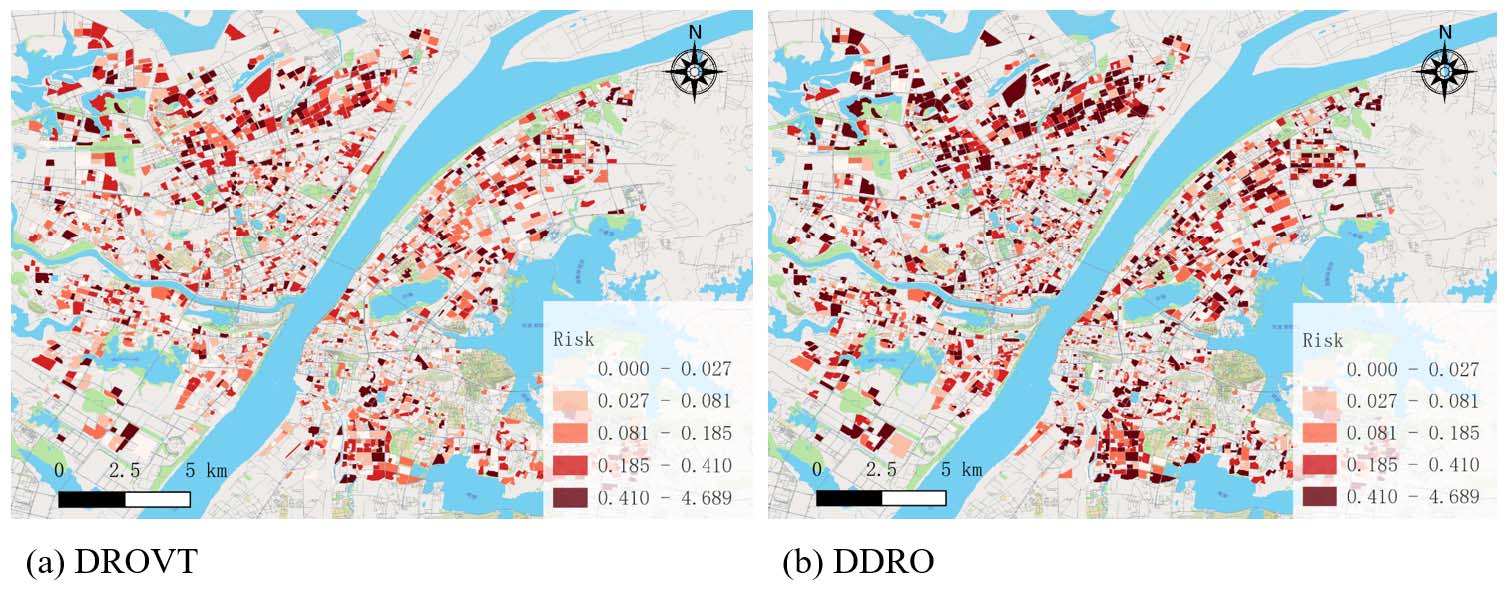
图12显示了基于距离的递送路由优化方法（DROVT）和DDRO结果中社区风险的空间分布。社区风险值介于0到 4.689之间。在DROVT结果中，具有高病毒传播风险的社区数量明显少于DDRO结果中的数量。特别是在新型冠状病毒肺炎确诊病例较多的武汉西北部，病毒传播风险显著降低。

C. 物资配送策略分析

1) 车辆容量的影响

车辆容量可能对生活物资配送路线产生重大影响。小型车辆将需要更多的出行

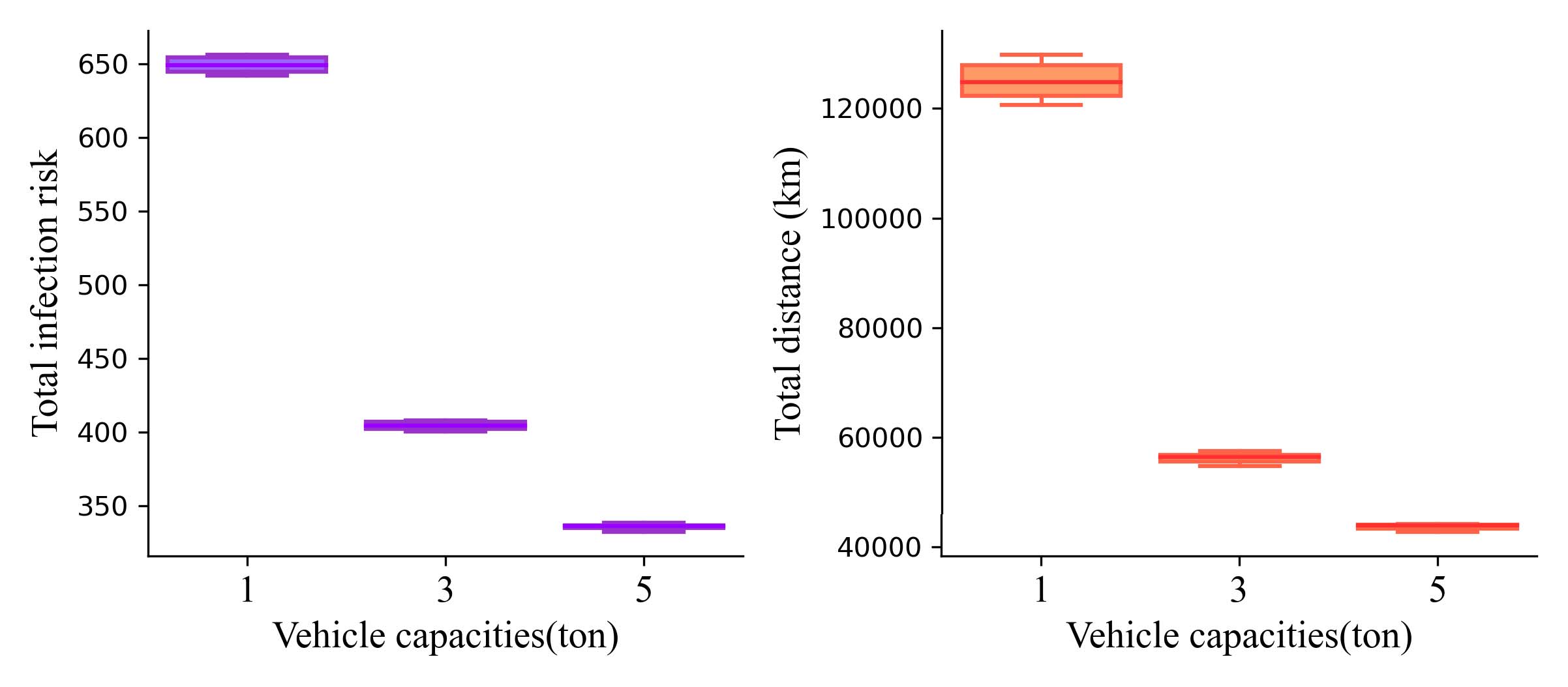
因此可能会增加病毒传播风险。通过设置不同的车辆容量，我们考察了其影响。所得结果的目标函数如图13所示。当车辆容量分别为1吨、3吨和5吨时，总病毒传播风险 δ分别为648.92、404.25和336.35，相应的总距离分别为 124,796.49千米、56,424.55公里和43,961.99千米。当车辆容量从1吨增加到5吨时，病毒传播风险降低了92.92%，总运输距离减少了121.17%。这些结果表明，较大的车辆确实能够降低病毒传播风险。

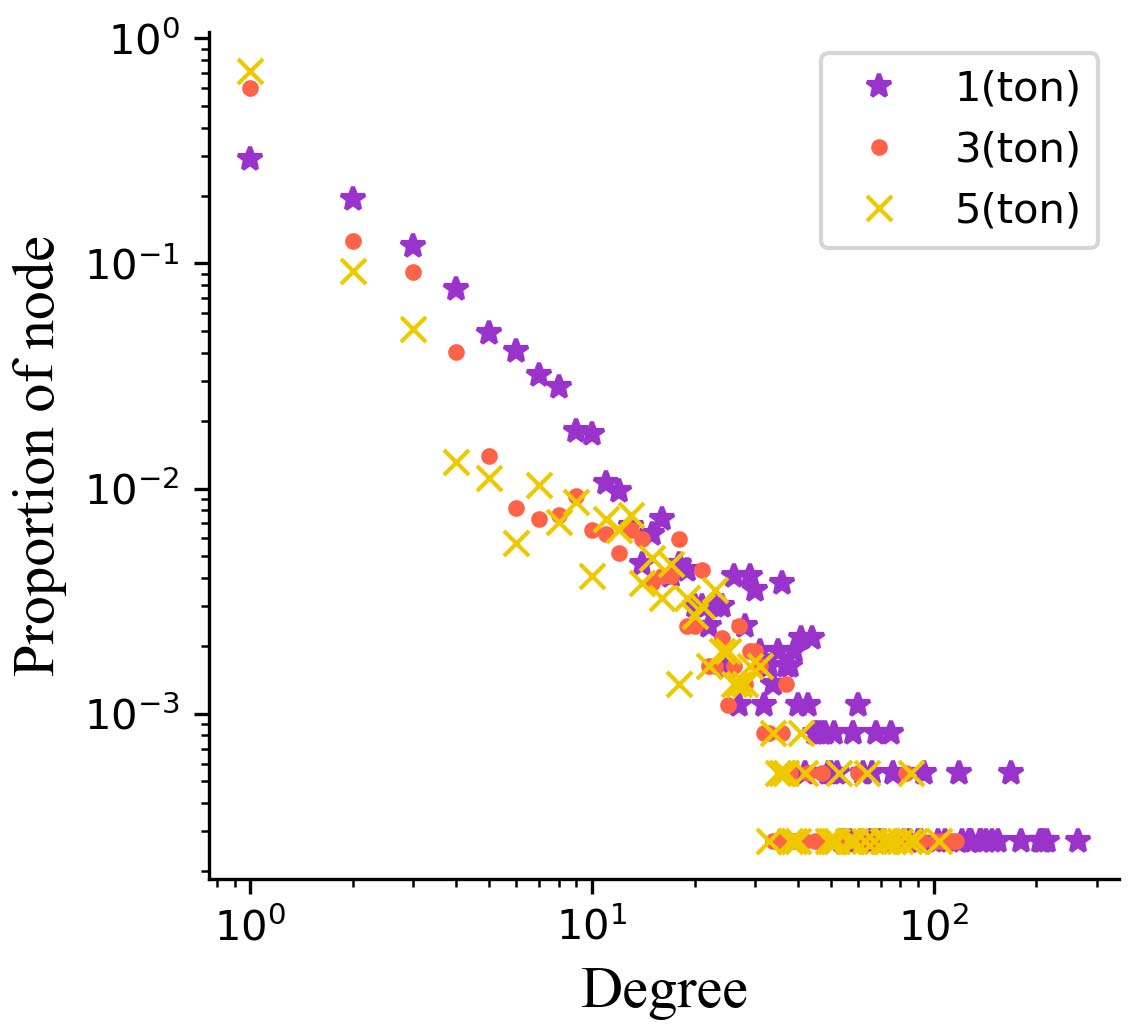
一个解决方案的配送路线构成一个复杂网络。由于车辆容量的不同，配送网络结构也会发生变化。通过统计节点度（即与该节点相连的路线段数量），可以衡量配送员与社区之间的必要接触情况。图14展示了不同容量下基于配送路线的网络的节点度分布。1吨容量情况下，相同节点度的节点比例明显高于5吨情况，换句话说，其包含的接触更多。

2) 交通管制的影响

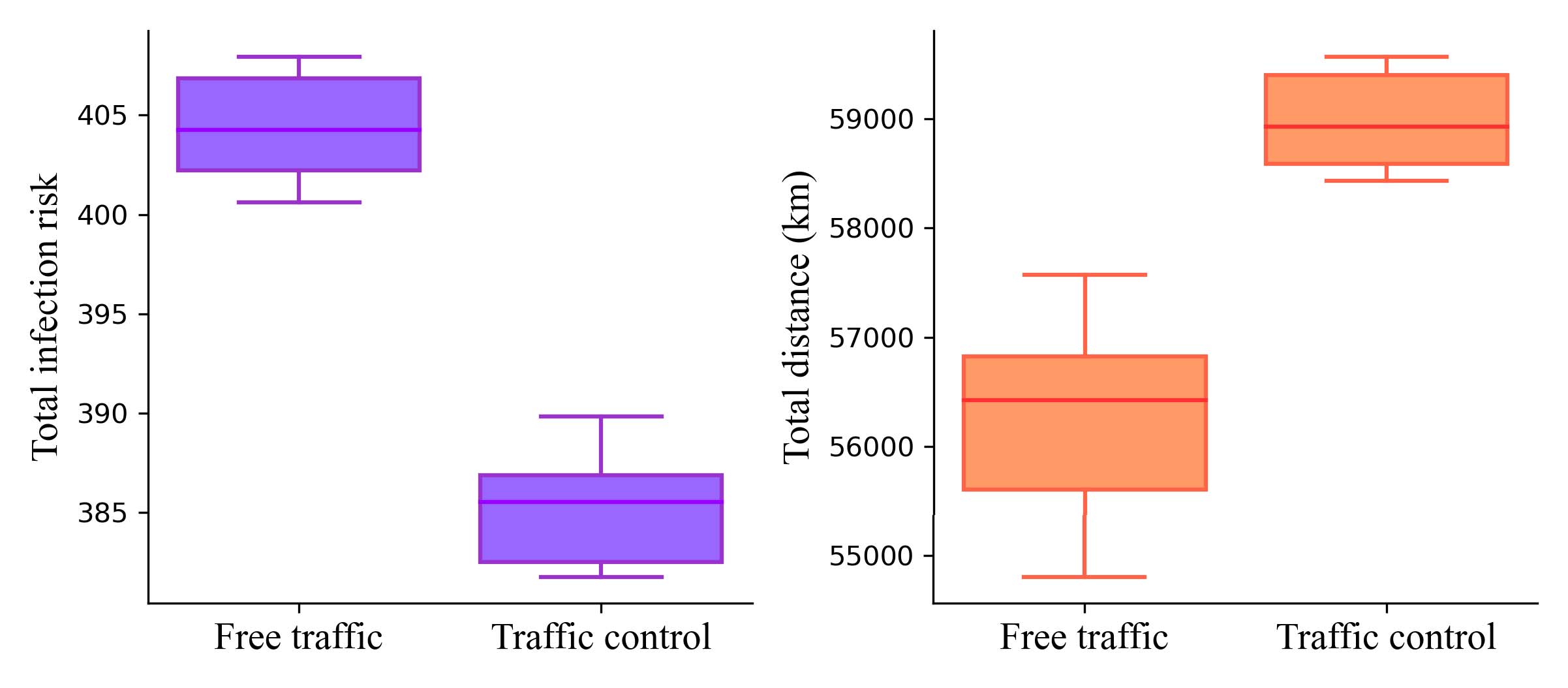
由于流行病学特征，确诊的新型冠状病毒肺炎病例会集中在城市的某些区域。实施交通管制，切断这些高风险区域之间的出行，可能是降低新型冠状病毒肺炎传播风险的有效手段。在此，我们选择两个高风险行政区——东西湖区和汉阳——实施出行管控。也就是说，这些区域内的车辆无法前往其他区域，反之亦然。所得结果如图15所示。在交通管制下，病毒传播风险中位数 δ将从404.25下降至385.52，降幅为4.63%。而总路线长度则从56,424.55公里增加到58,928.58公里。这些结果表明，交通管制策略能有效降低城市居民与配送员之间的新型冠状病毒肺炎传播风险。

3) 配送员个人防护的影响

个人防护水平也会影响生活物资配送过程中的新冠病毒感染风险。通过在公式5中设置不同的防护水平值（0.8、0.95 和 0.99），评估了个人防护的效果。结果如图16所示。当防护水平从0.80提高到0.99时，总新冠病毒传播风险从105.36下降至70.1。同时，总路线长度的中位数也从60,620.6千米减少到46,866.9千米。这表明更高的防护水平能够有效降低感染风险并优化配送效率。

个人防护将显著降低居民和配送员的感染风险，同时通过减少总行驶路线长度来提高配送效率。

六、结论

在新冠疫情暴发期间，生活物资配送对于保障居家隔离措施的有效实施至关重要。传统应急物流未考虑配送过程中可能带来的病毒传播风险。本研究提出了一种新的生活物资配送路径优化方法，充分考虑了配送过程中可能发生的新型冠状病毒肺炎传播风险。通过构建基于复杂网络的病毒传播模型，模拟居民与配送员之间的新冠病毒感染过程；并提出了一个兼顾新冠病毒感染风险和总路线长度的双目标模型，采用混合元启发式算法进行求解。在武汉开展的实验结果表明，935辆车共行驶56,424.55公里，为3,154个社区配送必要的生活物资，总风险为404.25，相比传统的基于距离的优化方法，新型冠状病毒肺炎传播风险降低了67.55%。

本研究仍存在一些局限性，例如无症状新冠病例、生活物资逐日配送。未来，我们将扩展基于复杂网络的病毒传播模型，以考虑感染原因由于无症状新冠病例。另一方面，所提出的方法将被扩展以适应多日生活物资配送。