LSTS算法硬件验证与授时设计

无线传感器网络时间同步的电路设计与物理实验

摘要

LSTS算法是一种针对抑制无线传感器网络（WSNs）中随机有界通信延迟的时间同步算法。理论分析表明，即使在存在随机延迟的情况下，该算法给出的所有传感器的漂移估计将以 1/k的速率渐近收敛于一个公共常数，其中k为离散时间，且全局同步误差是有界的。为进一步验证LSTS算法理论结果的有效性及其实际可行性，我们自主设计了一种硬件平台，并在此平台上通过与ATS和WMTS等其他算法在收敛速率、偏移补偿误差和同步误差等多个方面的比较，开展了物理实验。结果表明，LSTS算法在大多数性能指标上处于最先进的水平。最后，设计了“同步秒脉冲（SSP）+同步时间（ST）”的方法，为无线传感器网络提供授时服务，使得时间协议非常简单，同时也便于底层硬件进行时间获取，从而增强了其实用性和通用性。

Index Terms— 时间同步，FPGA，硬件平台，授时服务

引言

由于具有巨大的应用潜力和发展空间，无线传感器网络被广泛应用于环境监测和灾害预测等多个领域[1]。无线传感器网络的许多基本功能，如目标定位和数据融合，都需要在全局共同时钟下进行。传感器时钟的同步误差越小，网络的整体性能越好。因此，时间同步是无线传感器网络的基础支撑技术，甚至是许多实际应用和高技术的前提条件[2]。

受多智能体系统（MASs）一致性问题分析的启发，近年来提出了一些基于一致性的时间同步（CBTS）算法。谢纳托和菲奥伦蒂尼提出了一种自适应时间同步（平均时间同步）算法[5]。当数据传输无延迟时，该算法的时间同步误差呈指数级收敛。廖和Barooah提出了一种适用于无向马尔可夫跳变拓扑的时间同步算法[6]。通过假设相对测量噪声是对称的，他们证明了估计误差在均方意义下收敛。何、程、施、陈和孙提出了一种加权最大WMTS算法在无向拓扑[7],下抑制随机延迟，并证明了该算法的漂移估计误差期望是有限时间收敛的，且漂移估计误差是均方收敛的。但田、宗和曹的研究指出，上述所有算法在任意互连拓扑[8]下，只要网络中存在任意小的随机通信延迟，都会发散。进一步地，何提出了基于最小二乘估计的时间同步（LSTS）算法[9],[10]，即使存在有界随机延迟，该算法仍能保证漂移估计以 1/k的速率收敛（其中 k表示离散时间），并且同步误差是有界的。

尽管理论分析具有诸多优势，但任何时间同步算法的性能都需要通过严谨的物理实验进行验证。在实际工作中，无线传感器网络会遇到各种问题，如时间戳不准确和丢包，这些问题会影响时间同步算法的性能。然而，现有参考文献中报道的硬件平台和实验方法存在一些问题 [5],[11],[12]。首先，这些硬件平台的系统时钟频率较低，仅为32千赫兹。当系统时钟频率较低时，时间戳标记的精度也较低，这会人为地向硬件系统引入噪声。系统时钟周期是平台的最小时间分辨率。由于这些平台的频率较小，其最小时间分辨率较差，可能导致平台对算法是否发散不敏感。其次，目前尚无针对延迟对ATS、WMTS和 LSTS算法影响效果的比较研究。谢纳托和菲奥伦蒂尼已对无延迟情况下的ATS算法进行了系统测试[5]。当延迟较小时，何比较了ATS和WMTS算法[11],，姚比较了 ATS和LSTS算法[12]。但在延迟较大的情况下，这三种算法尚未进一步测试。即使在小延迟或无延迟的情况下，由于时间戳误差会影响算法，且硬件平台对算法是否发散不够敏感，实验结果缺乏说服力。最后，这些平台并未将时间同步算法转化为直接为底层硬件提供授时服务的方法。为了消除时间戳精度低的影响，提高算法的实用性和通用性，并深入研究ATS、WMTS和LSTS算法的性能，在实际工作中，设计一个高质量的硬件平台尤为重要。

本文的其余部分组织如下。第2节描述了总体电路设计。第3节描述了收发时间戳标记模块。第4节描述了内核模块的设计。第5节是定时模块的设计。第6节是物理实验的结果，第7节是结论。

II. 总体电路设计

我们自主设计了一个由多个节点组成的硬件平台。每个节点的电路主要由无线通信模块和处理器组成。无线模块选用TI公司的CC2420[13], （基于Zigbee的射频（ RF）收发器），处理器选用Xilinx的XC6SLX16 FPGA [14]。采用“FPGA+CC2420”的结构，其第一个优点是 CC2420在每次发送和接收数据包时，都会在帧起始定界符（SFD）引脚上产生一个上升沿信号。由于该信号来自 MAC层，因此FPGA进行时间戳标记的精度较高，且精度可控制在FPGA的一个系统时钟周期内。第二个优点是在 FPGA中可以设计多种外围电路，以提高电路的稳定性。

图1展示了节点的电路结构。从图中可以看出，该结构极为简单。

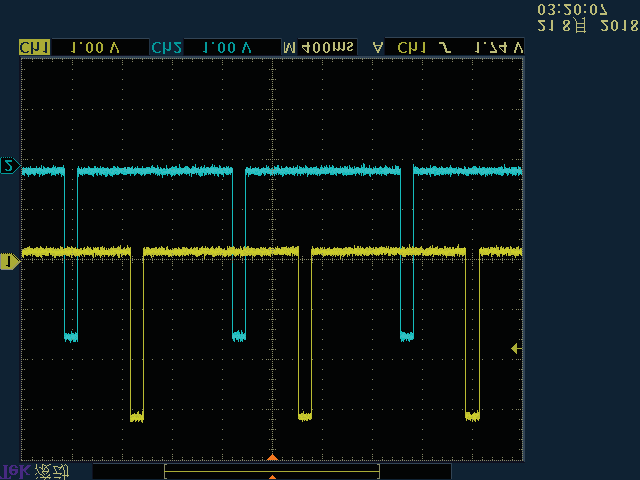
图2展示了在FPGA中设计的内部电路结构。从图中可以看出，FPGA的内部电路主要包括SPI收发器、收发时间戳标记模块、内核模块、算法模块和定时模块。各模块的主要功能如下。（1）SPI收发器。该模块用于完成内核模块与CC2420之间的通信，或内核模块与闪存之间的通信。（2）收发时间戳标记模块。该模块用于标记并存储相应的本地时钟用于数据包的发送和接收。（3）内核模块。该模块主要功能包括初始化CC2420，协调数据包的收发以避免时间冲突，并协调收发时间戳标记模块进行接收时间戳的标记和存储。此外，它还分析接收到的数据包，完成数据包的分发、存储和丢失处理。（4）算法模块。该模块用于计算时间同步算法中的变量，包括相对漂移、漂移补偿和偏移补偿。（5）定时模块。每当系统时钟的上升沿到达时，该模块计算并预测虚拟时钟，然后生成SSP和ST。

III. 收发时间戳标记模块

A. 接收时间戳标记

如图3所示，当节点接收到数据包时，SFD引脚的电平会发生变化。当检测到SFD引脚的上升沿信号时，FPGA立即标记其本地时钟，从而完成时间戳标记。FPGA的系统时钟频率选择为50MHz（1个时钟滴答=20 ns），因此标记精度为20纳秒，基本消除了时间戳误差。需要注意的是，当节点发送数据包时，SFD引脚电平的变化与接收时相同。

当节点发送数据包时，SFD引脚也会产生一个上升沿信号。为了避免遗漏接收时间戳标记，设计上采用了预标记和后处理的方法。预标记是指只要检测到SFD引脚的上升沿信号，标记模块就会预先打上一个接收时间戳。后处理在内核模块中进行，用于分析上升沿信号的来源。只有当该信号是由接收数据包引起时，时间戳才会被注册。每个节点以广播形式发送数据包，其他节点即使不是其邻近节点也会接收到该数据包。因此，后处理还需要读取数据包中的地址，并与节点存储的邻近地址列表进行匹配。如果匹配成功，则认为时间戳正确；否则，时间戳将被丢弃。通过修改邻近地址列表，可以构建任意的通信拓扑，因此该平台在测试算法时非常方便。

B. 发送时间戳标记

当节点发送数据包时，只有在数据包写入CC2420的 TXFIFO并启动传输后，SFD引脚才能产生上升沿信号。然而，发送时间戳无法与相应的数据包一起传输。我们采用以下方法来解决此问题。在发送数据包之前会打上一个发送时间戳，另一个时间戳则根据SFD引脚的上升沿进行标记。通过统计方法获得这两个时间戳之差的均值T0，并将该均值存储到程序中。之后每次发送数据包时，首先打上一个时间戳，然后加上 T0的均值，得到一个新的时间戳作为发送时间戳。该方法能够提高通信效率并降低丢包率，适用于大规模节点网络。

如图4所示，蓝色曲线为时间戳差值 T0，红色曲线为 T0的均值。在此硬件平台上，该方法的发送时间戳精度为3ticks，标签精度较高，能够满足设计要求。

IV. 内核模块

内核模块是内部电路的控制核心，采用有限状态机 (FSM)完成设计。图5显示了该模块的程序流程图。

A. 序列号更新模块

序列号更新模块是节点初始化的一个子模块。LSTS 算法使用固定的初始收发时间戳来计算相对漂移。当一个节点关闭后再开启时，其初始时间戳会发生变化，但邻近节点中存储的初始时间戳不会自动更新，这将导致系统运行错误。该问题在ATS和WMTS算法中不存在。为了解决上述问题，设计了一个序列号更新模块。序列号从闪存中自动读取，每次节点开机时自动加一。更新后的序列号一方面覆盖闪存中的原始序列号，另一方面每次随数据包一同发送。当节点 i首次接收到邻居节点j的数据包时，会存储节点 j的序列号。对于后续接收到的数据包，如果其序列号等于最初存储的序列号，则节点 i认为节点j未被关闭后重新开启；否则，节点 i认为节点 j已被关闭后重新开启。此时，节点 i将丢弃原先存储的收发时间戳，并将当前标记的时间戳作为新的初始时间戳。该设计无需额外通信次数，解决了LSTS算法的问题，从而保证了通信效率。

B. 发送控制模块和接收控制模块

内核模块可进一步分为发送控制模块和接收控制模块，分别对应图5中的左部和右部。为了避免运行干扰，我们采用添加标志位的方法，以方便两个控制模块之间的协调。Txflag(1:0)和Rxflag(1:0)分别用于表示两个控制模块的状态。表I展示了Txflag和Rxflag所代表的含义。

	Txflag(1:0)		Rxflag(1:0)
Bit	1	0	1	0
含义	启动标识符 发送	传输 标识符	启动标识符 接收的	接收 标识符

控制模块
控制模块

当定时发送命令到达时，发送控制模块被触发，然后该模块检测接收控制模块此时是否正在运行。只有当接收控制模块未运行时，发送控制模块才能打上发送时间戳，将数据包写入TXFIFO，并将Txflag(1)置为1。从打上发送时间戳到数据包写入TXFIFO这段时间内，节点有可能接收到数据包。因此，在发送数据包时，需要检测SFD引脚的电平。当SFD引脚为低电平时，发送控制模块可以发送数据包，并将Txflag(0)置为1。当SFD引脚电平为高电平时，需要停止当前轮次的传输，清除已写入TXFIFO的数据包，将发送标志(1)置为0，然后返回空闲状态。

接收控制模块由SFD引脚的上升沿信号触发。当数据包成功发送时，SFD引脚将产生一个上升沿信号，接收控制模块也会被触发。为了避免运行错误，接收控制模块需要根据Txflag的值来判断发送控制模块的状态。Txflag=“00”表示发送控制模块处于空闲状态，此时接收控制模块可以读取CC2420中RXFIFO的数据包，并将 Rxflag(1)置为1。Txflag=“01”未使用。当Txflag=“10”时，表示发送控制模块已被启动，但由于SFD引脚为高电平，发送控制模块停止发送并返回空闲状态，此时接收控制模块需要等待发送控制模块完成运行。当Txflag=“11”时，表示发送控制模块正在发送数据包，因此接收控制模块需要释放时间戳并返回空闲状态。

读取数据包后，需要根据邻近地址列表判断其是否来自邻近节点。如果该数据包来自邻近节点，则将该数据包和接收时间戳存储并分发到相应的计算模块；否则，将其丢弃。

V. 定时模块

“SSP + ST” 是提供授时服务最基础且应用最广泛的方法。例如，全球定位系统(GPS)和北斗导航卫星系统 (BDS)均采用该方法提供授时服务。该方法使得时间协议非常简单，并且使底层硬件获取时间变得极为方便。基于三种算法，设计了“SSP + ST”方法以提供授时服务。

生成SSP需要解决的首要问题是：每当系统时钟的上升沿到达时，是否能够产生一个虚拟时钟，即能否生成连续的离散虚拟时钟。如果始终按照三种算法的公式进行虚拟时钟的计算，显然在一个系统时钟周期内这是不可能实现的。我们采用“周期计算+预测”的方案来解决这一问题。如图6所示，为生成连续离散虚拟时钟的电路结构。

图6中的虚拟时钟计算模块是“周期计算”。该模块每1秒启动一次，然后根据三种算法的公式计算虚拟时钟。“周期计算”只能得到特定时刻的虚拟时钟，而图中所示的“预测”部分可以计算特定时刻中间的虚拟时钟。每当系统时钟的上升沿到来时，本地时钟加一，虚拟时钟则加上漂移补偿。由于虚拟时钟没有小数部分，因此漂移补偿 drift_cmpen(39:0) 需要被分为两部分：整数部分 drift_cmpen(39) 和小数部分 decimal_drift_cmpen(38:0)。每当系统时钟的上升沿到来时，每个加法器启动一次，从而实现对连续离散虚拟时钟时间同步的预测。由于“预测”是通过加法器实现的，虚拟时钟可在单个系统时钟周期内完成计算。

当获得连续的离散虚拟时钟后，可轻松生成SSP和 ST。ST可以进一步以协调世界时（UTC）的形式表示，并通过通用异步收发传输器输出，从而提供授时服务。

VI. 实验结果

A. 时间同步算法理论

我们在该硬件平台上实现了ATS、WMTS和LSTS算法，并对这些算法进行了系统比较。

在此模型的时间同步过程中，节点i以伪周期形式广播其自身的数据包，包括漂移补偿、偏移补偿和发送时间戳。当节点 j接收到邻居节点 i发送的数据包时，立即标记其本地时钟，即接收时间戳，然后结合先前接收到的数据包更新漂移补偿和偏移补偿。三种算法的具体公式可参考[8]。

对于这三种算法，[8]中的定理1和定理7给出了以下结论。

声明1。 当存在有界随机延迟时，以下陈述成立，其中 k表示离散时间：（1）在ATS算法下，相对漂移估计误差不收敛；（2）在WMTS算法下，相对漂移估计误差以 1/√k的速率收敛；（3）在任何CBTS算法下，相对漂移估计误差的最大收敛速率为 1/k。

对于LSTS算法m，以下声明由[10]中的定理m1和定理m2给出。

声明2。 即使存在有界随机延迟，LSTS算法也能确保无线传感器网络中所有节点的漂移估计渐近收敛到一个公共常数。所有节点的漂移估计误差的收敛速度为 1/k。并且LSTS算法能确保任意两个节点之间的偏移补偿误差和同步误差始终有界。

我们将通过在我们平台上的物理实验来验证这些声明。

B. 三种算法的比较

物理实验使用15个节点构成如图7所示的网格通信拓扑。表II显示了三种算法的参数设置，其中这些符号的含义可参考[8]。在这些实验中，延迟为3微秒量级，广播包周期为2秒，1个时钟滴答为20纳秒。

算法	ρe	ρa	ρb
ATS	0.5	0.5	0.5
WMTS	1/(1+l)	1	1
LSTS	l²/(1+⋯+l²)	0.5	0.5

图8显示了三种算法的相对漂移估计误差。当存在随机延迟时，ATS算法不收敛，而WMTS算法和LSTS算法均收敛。如图9所示，当存在随机延迟时，WMTS算法的误差以1/√k的速率渐近收敛，而LSTS算法以 1/k的速率渐近收敛。

图10显示了ATS算法的偏移补偿误差和同步误差。需要注意的是，我们使用max‖βi(k)−βj(k)‖ 和 max‖τ̂i(k)−τ̂j(k)‖ 分别表示网络的偏移补偿误差和同步误差，其中 βi(k) 和 τ̂i(k) 分别表示节点 i在 k时刻的偏移补偿和虚拟时钟。从该图可以看出，即使随机延迟处于微秒级，ATS算法的偏移补偿误差和同步误差仍持续累积。

图11显示了WMTS算法和LSTS算法的偏移补偿误差。从图中可以看出，当存在随机延迟时，WMTS算法的偏移补偿误差会持续累积，而LSTS算法的偏移补偿误差不会累积。

图12显示了WMTS算法和LSTS算法的同步误差。从该图可以看出，WMTS算法比LSTS算法更早趋于稳定，但LSTS算法的同步误差更低。当延迟处于3微秒级别时，WMTS算法的同步误差稳定在16微秒，而LSTS算法的同步误差稳定在12微秒，比WMTS算法低4微秒。综上所述，LSTS算法更优。

C. 定时服务

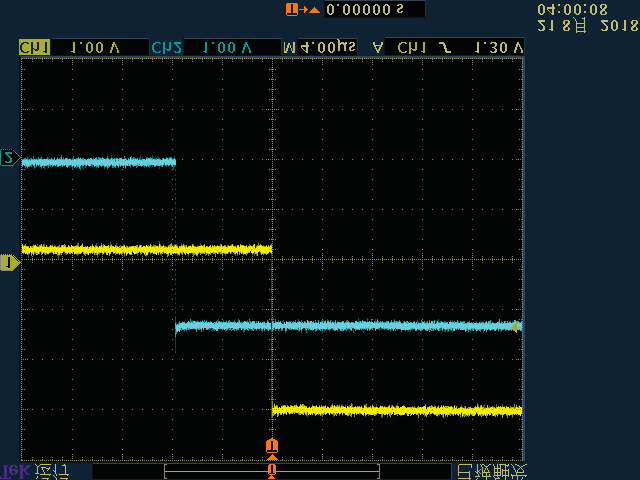
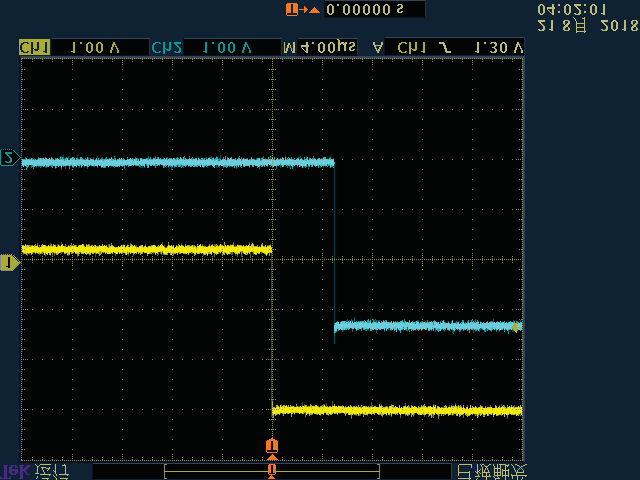
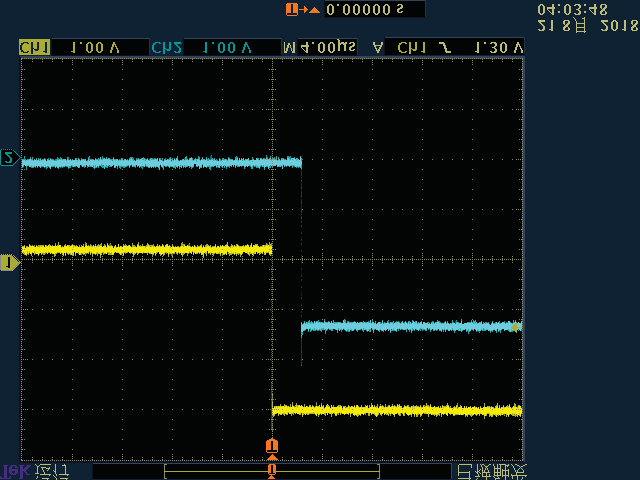
在图7所示的网格拓扑中，当延迟为3微秒级别时，测试了节点间同步信号脉冲（SSP）的同步误差。实验结果如图13所示。图中的第一个子图显示了LSTS算法尚未同步时节点间的SSP，其余子图显示了同步完成后的节点间 SSP。以节点1产生的黄色SSP作为参考信号，将其与其他节点的蓝色SSP进行比较。从该图可以看出，当LSTS算法稳定后，在不同时间点，节点5、节点11和节点15相对于节点1的同步误差分别为8微秒、4.8微秒和2.4微秒。

VII. 结论

我们设计了一个高质量的硬件平台，用于研究ATS、WMTS和LSTS算法的性能。通过一系列物理实验，我们表明实验结果与[8],[10],中的理论分析一致，且LSTS算法在大多数性能指标上处于最先进的水平。基于LSTS算法，我们首次设计了一种“SSP + ST” 方法来提供授时服务。我们测试了同步信号脉冲（SSP）的同步误差，结果表明同步误差较低且稳定。这使得该硬件系统不仅在无线传感器网络领域有用，而且在其他需要高时间同步精度的工业领域也有用。