MX 模拟赛九总结

最新推荐文章于 2025-12-04 23:33:43 发布

原创最新推荐文章于 2025-12-04 23:33:43 发布 · 653 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法

比赛总结专栏收录该内容

27 篇文章

订阅专栏

T1

题面：

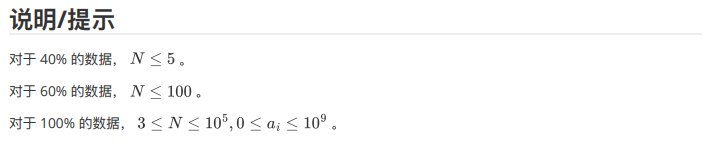
题目写的有点鬼畜，但是通过样例能看出来意思应该是找到满足题目条件的两个端点，然后算这个端点距离的一般是多少。

然后就成了一道非常水的题。

自己看代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,a[100006];
signed main()
{
//	freopen("village.in","r",stdin);
//	freopen("village.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	sort(a+1,a+n+1);
	int mn=1e18;
	for(int i=2;i<n;i++)
	{
		int l=-1,r=-1;
		if(i==2)
		{
			l=1;
		}
		else if(a[i-1]-a[i-2]>a[i]-a[i-1])
		{
			l=i-1;
		}
		if(i==n-1)
		{
			r=n;
		}
		else if(a[i+2]-a[i+1]>a[i+1]-a[i])
		{
			r=i+1;
		}
		if(l==-1||r==-1)
		{
			continue;
		}
		mn=min(mn,a[r]-a[l]);
	}
	double ans=mn*1.0/2;
	printf("%0.1lf",ans);
	return 0;
}

T2

题面：

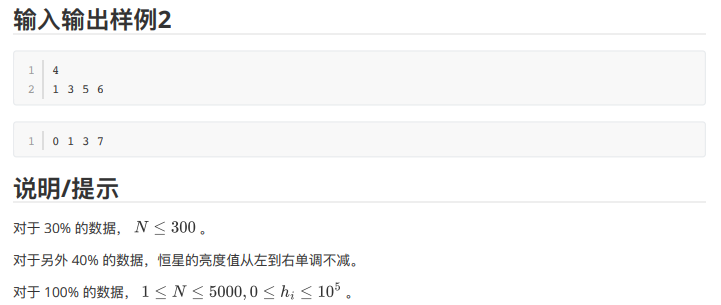
其实这道题不难想到：如果我们算出了 $[l, r]$ 的不对称值，那么我们就可以算出 $[l - 1, r + 1]$ 的不对称值。因此这道题就是一个类似于 DP 的做法。并且数据范围支持 $O(n^2)$ ，所以我们先枚举长度，再枚举对称中心，然后转移一下 DP，再求一下最小值。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,a[5006],b[10006],c[5006][5006];//c[i][j] 表示以 j 为对称中心，且 r-l=i 时的不对称值
signed main()
{
//	freopen("star.in","r",stdin);
//	freopen("star.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=n;i++)
	{
		if(i==1)
		{
			cout<<0<<" ";
			continue;
		}
		if(i&1)//对称中心在数上
		{
			int ans=1e18,r=(i+1)/2;
			for(int j=r;j<=n-r+1;j++)
			{
				c[i][j]=c[i-2][j]+abs(a[j-r+1]-a[j+r-1]);
				ans=min(ans,c[i][j]);
			}
			cout<<ans<<" ";
		}
		else//对称中心在数之间
		{
			int ans=1e18,r=i/2;
			for(int j=r;j<n-r+1;j++)
			{
				c[i][j]=c[i-2][j]+abs(a[j-r+1]-a[j+r]);
				ans=min(ans,c[i][j]);
			}
			cout<<ans<<" ";
		}
	}
	return 0;
}

T3

题面：

明显的组合数学题。

考试的时候其实我已经把大部分都想出来了，只是最后有一点没想到，遗憾 30pts。

原题：https://www.luogu.com.cn/problem/P8398。

直接给大家看我写的题解吧：

看到题解区有很多正难则反的做法，这里给出一种直接算的方法（而且不用分环的奇偶）。

首先我们随机钦定一个点，并标记出圆心：

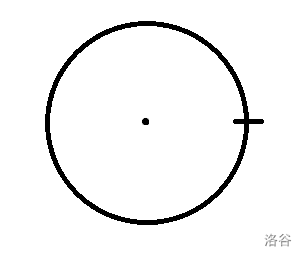
我们过这个钦定的点做它的直径：

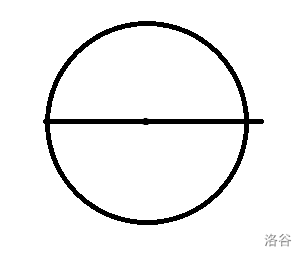
这时我们很容易发现：如果说另外两个点都在这条直径的上面或都在下面，那肯定没法构成合法的三角形。所以我们要把上面的点和下面的点连起来构成三角形。

因此设直径上面的点数为 $c n t 1$ ，下面的点数为 $c n t 2$ ，那么可以算出总共有 $cnt1\times cnt2$ 种三角形。

但是这只是一个很粗劣地估计，因为有可能会出现这种情况：

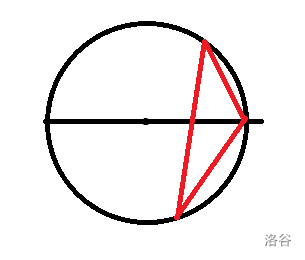
我们把这种情况提出来单独分析：

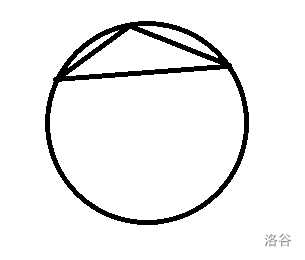
我们不难发现：这种三角形中必然有一个点，使得其他两个点都在它的逆时针方向，而且这两个点都在这个点的直径的一侧。换而言之就是有这种情况：

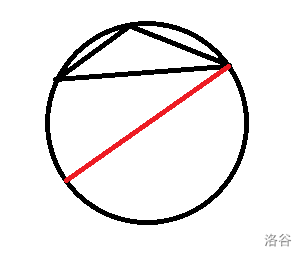
而且我们也能看出来：每个不合法的三角形只被算过一次。

所以我们可以理解为对于所有点，我们求它们的直径的同一侧有多少个三角形。注意：只求同一侧。不然一个三角形就会被算两遍。

现在的问题就是这个半圆里究竟有多少个三角形（就是这里考试的时候没想通）。

我们假设这个半圆内有 $c n t$ 个点（包含当前点对面的点），那么我们从中随机选出两个点和当前点进行搭配，就会有 $C_{cnt}^2$ 种方案，但是有可能会在同一个位置重复选两个点，所以应该有 $C_{cnt}^2-\sum_{j=i}^{i+\frac{c}{2}}C_{a_j}^2$ 种方案。

很明显，后面那一块可以前缀和预处理出来，于是就变成了这样：

$(C_{cnt}^2-s_{i+\frac{c}{2}}+s_{i-1})\cdot a_i$

对于每个点，我们都求一次它的值。然后用我们上面的那个式子减它。

最终你会发现：这份代码其实过不了样例。原因很简单，画一个正确解的情况出来你就会发现：每个顶点都算了一遍当前这个合法的三角形。所以对答案除以 $3$ 就行了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,c,a[1000006],s[2000006],s1[2000006];
int C(int x,int y)
{
	if(y==1||y==0)
	{
		return 0;
	}
	return y*(y-1)/2;
}
signed main()
{
	cin>>n>>c;
	for(int i=1,x;i<=n;i++)
	{
		cin>>x;
		a[x]++;
	}
	s[0]=a[0];
	s1[0]=C(2,a[0]);
	for(int i=1;i<2*c;i++)//前缀和，这里断环成链了
	{
		s[i]=s[i-1]+a[i%c];
		s1[i]=s1[i-1]+C(2,a[i%c]);
	}
	int ans=0,r=c/2;
	for(int i=0;i<c;i++)
	{
		ans+=(s[i+r-(!(c&1)?1:0)]-s[i])*(s[i+c-1]-s[i+r])*a[i];//这里关于对面的点稍微调整一下就行了
	}
	for(int i=0;i<c;i++)
	{
		if(s[i+r]-s[i]==1)
		{
			continue;
		}
		ans-=(C(2,s[i+r]-s[i])-(s1[i+r]-s1[i]))*a[i];
	}
	cout<<ans/3;
	return 0;
}

T4

题面：

对于找到尽可能多的 bessie，我们很容易想到他肯定具有贪心性。因此我们可以枚举起点、枚举终点，然后贪心的找中间有多少个 bessie，于是我们有了 30pts（考试时在字符串前面多加了一个空格，结果写循环时写成从零开始了，痛失 30pts）。

然后考虑优化一下。我们从上面的思路很容易联想到最长上升子序列这类的问题。因为它们的宗旨都是找到前面的一个地方接上当前位置的数，然后求最大值。

于是我们可以定义 $f_{i,j}$ 表示以第 $i$ 个字符结尾且第 $i$ 个字符在 bessie 中充当第 $j$ 个字符时 bessie 数量最多多少。那么如果当前这一位是 e，我们就可以往前找到一个充当倒数第二个字符的位置然后接在一起，这样就又会形成一个 bessie。

但是这会有一个很大的问题，从第一个样例就能看出来：bessiebessie，很明显，前八个字符中只有一个 bessie，但是我们上面的 DP 转移会告诉我们第八个 e 可以和前面的 bessi 拼在一起，形成第二个 bessie。但是这明显是不可能的。因此我们需要稍微改一下 DP 状态：

设 $f_{i,j}$ 表示以第 $i$ 个字符结尾且第 $i$ 个字符在 bessie 中充当第 $j$ 个字符时 bessie 的第一个字符的位置在哪。当然，为了满足贪心性，我们的第一个字符的位置肯定会尽可能的靠近最后一个字符。这样，在我们转移完之后，我们就可以取最靠前的可以作为结尾的 e 来构成 bessie，至于后面接上的一概不管。这样就有 60pts 了。

最后我们考虑一下满分做法：对于满分做法，我们肯定是要 $O (1)$ 或者 $O(\log)$ 找到我们要找的那个位置。这里 $O (1)$ 明显可做，因此用 $O (1)$ 优化一下就行了。

简单说一下 $O (1)$ 怎么优化：我可以设 $la_i$ 表示上一个 $i$ 字符在字符串中出现的位置，比如说我当前到了一个字符 b，那么我就可以直接写 $la_0=i$ 。如果我到了 e，这时就有点麻烦了，因为 e 可以充当第二个和最后一个位置，这里我们遵循先更新靠后的。因为如果你先更新靠前的，那么当前这个字符有可能会被同时当作两个位置的字符算。

代码（异常简洁）：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,ans,la[6],dp[300006];
string s;
signed main()
{
	cin>>s;
	n=s.size();
	s=" "+s;
	for(int i=1;i<=n;i++)
	{
		if(s[i]=='b')
		{
			la[0]=i;
		}
		if(s[i]=='e')
		{
			la[5]=la[4];
			la[1]=la[0];
		}
		if(s[i]=='s')
		{
			la[3]=la[2];
			la[2]=la[1];
		}
		if(s[i]=='i')
		{
			la[4]=la[3];
		}
		if(!la[5])
		{
			continue;
		}
		dp[i]=dp[la[5]-1]+la[5];
		ans+=dp[i];
	}
	cout<<ans;
	return 0;
}

T5

题面：

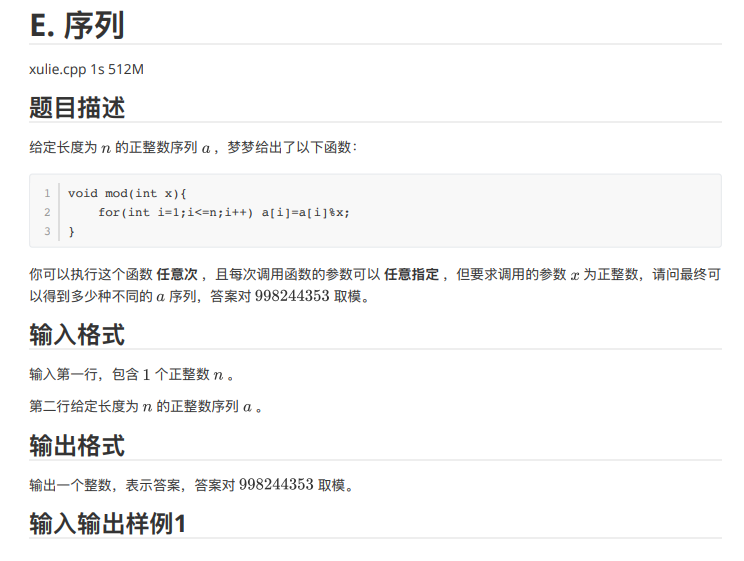
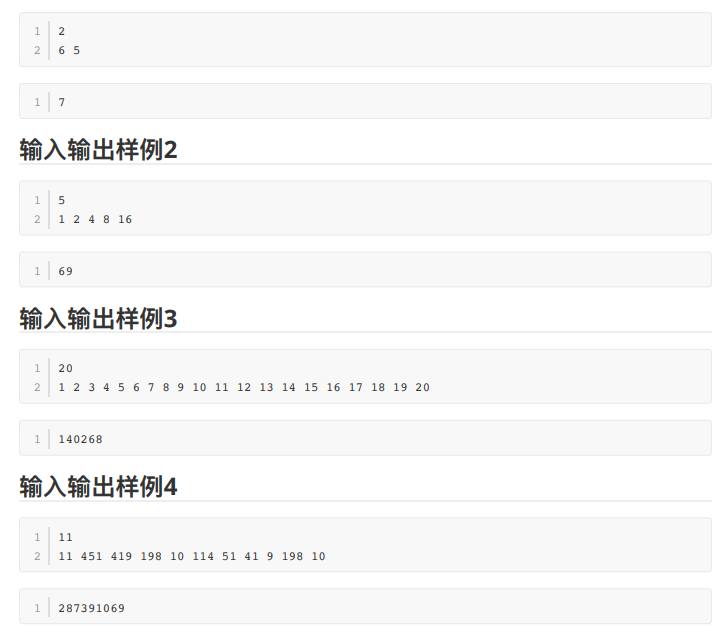
原题好像是 Anton Trygub Contest 2 Editorial 的 K 题，全网只搜到一篇题解（好像还是口胡过去的），还有就是官方题解了（但现在不是了，我们班才有一个同学写了这道题的题解，再加上我马上现在正在写的）。

前面有很多废话，我不想多说，给大家看看官方题解写的：

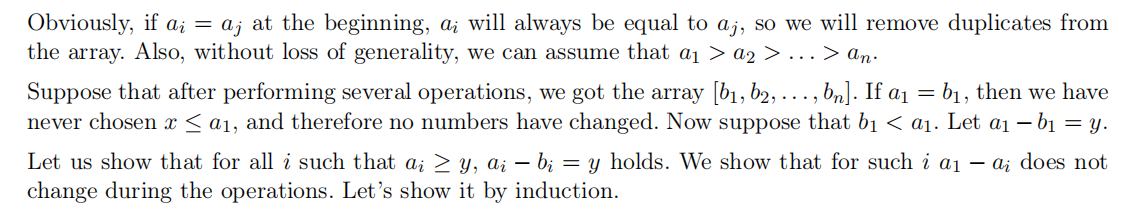
大致意思就是指我们会发现如果 $a_i=a_j$ ，那么它们的最终结果一定是一样的，所以我们先排序再去重。这里假定 $a_1\ge a_2\ge\dots\ge a_n$ （为了使逻辑更加严谨，此处稍作修改了一下）。

我们设原数列最终的结果是 $b_1,b_2,\dots,b_n$ ，如果说 $b_1=a_1$ ，说明我们选的 $x\gt a_1$ ，这时所有数都不会变，因此我们只需要考虑 $x\le a_1$ 的情况，那么可以得到 $b_1\lt a_1$ ，我们设 $y=a_1-b_1$ 。

然后通过神秘的手摸样例我们可以发现这样一个事：如果 $a_i\ge y$ ，那么 $a_i-b_i=y$ ，且 $a_1-a_i$ 保持不变。

然后就是证明。

但是官方题解的证明写的稍微有点跳跃，这里给大家看看我的证明方法。

首先我们假设 $a_1\bmod x_1\bmod x_2\bmod\dots\bmod x_m=b_1$ ，那么我们现在考虑一个 $a_1'=a_1\bmod x_1$ ，再考虑一个 $a_i'=a_i\bmod x_1$ ，于是我们可以得到 $a_1'\bmod x_2\bmod x_3\bmod\dots\bmod x_m=b_1$ ，所以 $b_1\le a_1'$ ，这是很明显的。

然后我们就可以开始列不等式了：

设 $a_1=k_1x_1+a_1',a_i=k_ix_1+a_i'$ ，则：

$\therefore a_1\ge a_i\ge y \\ \therefore k_1x_1+a_1'\ge a_i\ge a_1-b_1 \\ \because a_1'=a_1\bmod x_1 \\ \therefore a_1'\lt x_1 \\ \therefore(k_1+1)x_1\gt k_1x_1+a_1'\ge a_i\ge k_1x_1+a_1'-b_1 \\ \because a_1'\ge b_1 \\ \therefore (k_1+1)x_1\gt a_i\ge k_1x_1 \\ \therefore \lfloor\cfrac{a_i}{x_1}\rfloor=k_1 \\ \therefore a_i=k_1x_1+a_i' \\ \therefore a_1-a_i=k_1x_1+a_1'-k_1x_1-a_i'=a_1'-a_i'$

然后我们就可以得到：

$a_1-a_1'=a_i-a_i'$

这时我们令 $a_1=a_1',a_i=a_i'$ ，那么理论上来讲我们可以得到这样一个式子：

$a_1'-a_1''=a_i'-a_i''$

但是这有一个前提： $a_i'\ge a_1'-b_1$ 。现在我们再来证明一下这个：

设 $a_1-a_1'=a_i-a_i'=z$ ，则：

$\therefore a_1'=a_1-z,a_i'=a_i-z \\ \because a_i\ge a_1-b_1 \\ \therefore a_i-z\ge a_1-z-b_1 \\ \therefore a_i'\ge a_1'-b_1$

得证。

于是我们就可以把这个等式一直推下去：

$a_1-a_1'=a_i-a_i' \\ a_1'-a_1''=a_i'-a_i'' \\ a_1''-a_1'''=a_i''-a_i''' \\ \dots \\ a_1^{(m-1)}-b_1=a_i^{(m-1)}-b_i$

因为每一层的证明都和上面一模一样，所以我们可以用归纳法得出后面所有的等式全部成立。

所以说 $a_1-a_i$ 的差一直相等，所以保持不变。

然后我们把上面所有的等式左右加起来，就可以得到：

$a_1-b_1=a_i-b_i=y$

所以说，把 $a_i$ 变成 $b_i$ ，实际上就是减了个 $y$ ，或者换句话说：因为 $b_1\lt\frac{a_1}{2}$ （请读者自证），所以 $y\gt\frac{a_1}{2}$ ，所以实际上可以理解为对 $y$ 取模。

所以对于所有 $a_i\ge y$ 的 $i$ ，它们的差是固定不变的，我们都不用算它们的方案数，因此我们只需要知道 $a_i\lt y$ 的 $i$ 能构成的方案数有多少就行了。

因此我们可以设 $f_{i,j}$ 表示当前在第 $i$ 个位置，且 $x\isin[j,501]$ 之间时的方案数。然后枚举 $i$ ，枚举当前这一位的 $b$ ，于是可以得到 $y=a_i-b$ ，然后找到最后一个小于 $y$ 的位置，从它转移过来（如果找不到就自己单独成一种方案）。

于是就可以写出代码了：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353;
int n,a[506],la[506],f[506][506];
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	sort(a+1,a+n+1);
	n=unique(a+1,a+n+1)-a-1;
	for(int i=1;i<=n;i++)
	{
		f[i][501]=1;
		//如果 x=501，那么所有数都不会变，所以必定有一种方案，当然这里也可以写 max{a}+1
		for(int b=0;b<(a[i]+1)/2;b++)
		{
			int y=a[i]-b;
			int it=lower_bound(a+1,a+n+1,y)-a-1;
			if(!it)//单独成一种方案
			{
				f[i][y]++;
			}
			else
			{
				for(int j=b+1;j<=501;j++)
				//枚举一下第 it 个位置的下限是多少
				//当然这个下限肯定不能小于等于 b，不然这一位不可能是 b，而是会比 b 小
				{
					f[i][min(y,j)]=(f[i][min(y,j)]+f[it][j])%mod;
				}
			}
		}
	}
	int ans=0;
	for(int i=1;i<=501;i++)//统计答案
	{
		ans=(ans+f[n][i])%mod;
	}
	cout<<ans;
	return 0;
}