前言
好久没写总结了,今天来更一下。
T1
题面:

看到求区间和,很容易想到求前缀和,我们假设 si=∑j=1iajs_i=\sum_{j=1}^ia_jsi=∑j=1iaj,那么对于一段区间和,就可以用 sj−sis_j-s_isj−si 来表示,现在我们要让这个差最大,因此我们可以选择固定 jjj 找最小的 sis_isi,也可以固定 iii 找最大的 sjs_jsj,换而言之,就是对于任意一个确定的位置 iii,我们要找到 max(si−minj=1i−1{sj},maxj=i+1n{sj}−si)\max(s_i-\min_{j=1}^{i-1}\{s_j\},\max_{j=i+1}^n\{s_j\}-s_i)max(si−minj=1i−1{sj},maxj=i+1n{sj}−si),因此我们只需要求出前缀和,然后预处理出后缀最大和前缀最小值就可以了。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,a[200006],s[200006],mn[200006],mx[2000006];
signed main()
{
// freopen("sum.in","r",stdin);
// freopen("sum.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
s[i]=s[i-1]+a[i];
}
for(int i=1;i<=n;i++)
{
mn[i]=min(mn[i-1],s[i]);
}
mx[n+1]=-0x3f3f3f3f3f3f3f3f;
for(int i=n;i>=1;i--)
{
mx[i]=max(mx[i+1],s[i]);
}
for(int i=1;i<=n;i++)
{
cout<<max({s[i]-mn[i-1],mx[i+1]-s[i-1],mx[i+1]-mn[i-1]})<<" ";
}
return 0;
}
T2
题面:


首先我们肯定能有一个很暴力的想法:对于每一个合法的格子,我们以它为起点找与它距离大于等于 444 的格子有多少个,但是这样每一次扫会有大量的格子被重复扫到,时间复杂度明显很高。
其实手摸一下几组样例就很容易想到:每个格子的合法终点数是固定的。那我们为什么不能用一个数组记录下来每个格子的合法终点数,这样每次就不用把全程都扫完呢?这是一个明显可行的思路,但是有一点:每一个格子的合法终点数一定是大于等于它下一步能到的格子的合法终点数的和,也就是说有一些格子它只能作为当前这个格子的合法终点,不能作为这个格子下一步能到的格子的合法终点。因此我们可以考虑的更齐全一点:
设 bi,j,1/2/3/4b_{i,j,1/2/3/4}bi,j,1/2/3/4 表示从 (i,j)(i,j)(i,j) 走 1/2/3/≥41/2/3/\ge41/2/3/≥4 步能到的格子的个数,这样子就能很方便的转移了。
最后就是这个 bbb 怎么求的问题:其实很简单,对于每一条合法路径,我们都可以边 dfs 边更新 bbb 值,因为这个 bbb 是肯定不会变的,所以每个格子只用被扫一遍,时间复杂度 O(nm)O(nm)O(nm)。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=1e9+7;
int n,m,vis[1006][1006],b[1006][1006][6],mp[1006][1006],fx[4][2]={1,0,0,-1,-1,0,0,1};
int read()
{
int z=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')
{
f=-1;
}
c=getchar();
}
while(c>='0'&&c<='9')
{
z=z*10+c-'0';
c=getchar();
}
return z*f;
}
void dfs(int x,int y)
{
if(vis[x][y])
{
return;
}
vis[x][y]=1;
bool fl=false;
for(int i=0;i<4;i++)
{
int nx=x+fx[i][0];
int ny=y+fx[i][1];
if(nx<1||nx>n||ny<1||ny>m)
{
continue;
}
if(mp[nx][ny]-mp[x][y]!=2)
{
continue;
}
fl=true;
dfs(nx,ny);
for(int j=1;j<=4;j++)
{
b[x][y][j+1>4?4:j+1]=(b[x][y][j+1>4?4:j+1]+b[nx][ny][j])%mod;
}
}
if(!fl)
{
b[x][y][1]=1;
}
}
signed main()
{
n=read(),m=read();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
mp[i][j]=read();
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(!vis[i][j])
{
dfs(i,j);
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
bool fl=true;
for(int k=0;k<4;k++)
{
int nx=i+fx[k][0];
int ny=j+fx[k][1];
if(nx<1||nx>n||ny<1||ny>m)
{
continue;
}
if(mp[nx][ny]-mp[i][j]==-2)
{
fl=false;
break;
}
}
if(fl)
{
ans=(ans+b[i][j][4])%mod;
}
}
}
cout<<ans;
return 0;
}
其实还有另一种做法:首先建图,然后跑拓扑。一样可以做出来。
T3
题面:


第一眼看上去:没啥思路……
首先我们看一看数据范围中给的特殊情况:
- n=mn=mn=m:手算几组很容易发现:n=mn=mn=m 时只有两种情况。
- n+1=mn+1=mn+1=m:这就有点意思了,其实不难想到这种情况就是在 n=mn=mn=m 的基础上多增加了一列,但是具体情况还是要分类讨论一下。
看看第二种情况中我加粗的那段话,有没有想到点什么?
其实仔细思考不难想到:当 nnn 为偶数时其实就是很多个 n×nn\times nn×n 的小正方形拼在一起的,或者是在这些正方形中插入一些 n×1n\times1n×1 的长条形的矩形然后拼在一起。
但是通过我们的仔细观察其实不难发现:n×nn\times nn×n 的小正方形中有一种情况其实就是左右各加了一个 n×1n\times1n×1 的小矩形(见题中的图 2),因此当 nnn 为偶数时,我们也可以用 n×(n−2)n\times(n-2)n×(n−2) 的矩形组成它,于是这个题现在就变成了一个线性的问题了,可以直接用 DP 解决。
现在来看一下 nnn 是奇数该怎么解决。我们先举几个例子:
n=1n=1n=1:

n=3n=3n=3:
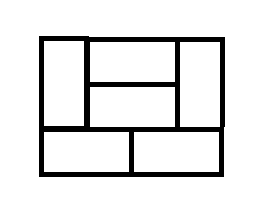

n=5n=5n=5:
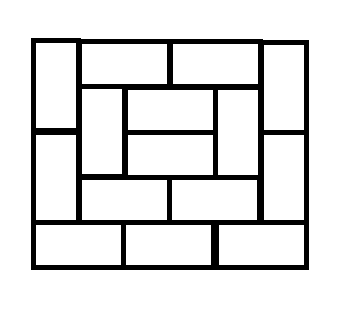
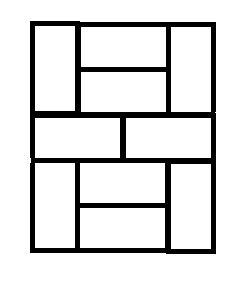
我们不难发现:当 nnn 为奇数时,每一次 nnn 扩大就是在原本的基础上再在外面套上一层“壳”,因此这也不难让我们想到可以把原本的大矩阵拆成好几个小的矩阵,每个矩阵的大小是多少呢?通过上面的例子我们不难发现:最基础的互不相干、互相不能转化的两种矩形分别是 n×(n+1)n\times(n+1)n×(n+1) 和 n×(n−1)n\times(n-1)n×(n−1),于是这又被我们转化成了一个简单的线性 DP 问题。
代码:
#include<bits/stdc++.h>
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353;
int n,m,dp[10000006][2];
signed main()
{
cin>>n>>m;
if(n>m)
{
swap(n,m);
}
if(n*m&1)
{
cout<<0;
return 0;
}
if(n==1)
{
cout<<1;
}
else if(n==2)
{
// vector<vector<int>>v(m+6,vector<int>(2,0));
dp[0][0]=0,dp[0][1]=1;
for(int i=1;i<=m;i++)
{
dp[i][1]=(dp[i][1]+dp[i-1][0]+dp[i-1][1])%mod;
if(i>=2)
{
dp[i][0]=(dp[i][0]+dp[i-2][1])%mod;
}
}
cout<<(dp[m][0]+dp[m][1])%mod;
}
else if(n&1)
{
// vector<int>dp(m+6,0);
dp[0][0]=1;
for(int i=1;i<=m;i++)
{
if(i>=n-1)
{
dp[i][0]=(dp[i][0]+dp[i-(n-1)][0])%mod;
}
if(i>=n+1)
{
dp[i][0]=(dp[i][0]+dp[i-(n+1)][0])%mod;
}
}
cout<<dp[m][0]*2%mod;//因为奇数的情况下所有矩形上下翻转一遍也可以形成一种新的方案
}
else//但偶数就没有这种性质,因为偶数的上下是对称的
{
// vector<vector<int>>dp(m+6,vector<int>(2,0));
dp[0][0]=dp[0][1]=1;
for(int i=1;i<=m;i++)
{
dp[i][1]=(dp[i][1]+dp[i-1][0])%mod;
if(i>=n)
{
dp[i][0]=(dp[i][0]+dp[i-n][1])%mod;
}
if(i>=n-2&&n-2!=0)
{
dp[i][0]=(dp[i][0]+dp[i-(n-2)][1])%mod;
}
}
cout<<(dp[m][0]+dp[m][1])%mod;
}
return 0;
}
T4
题面:

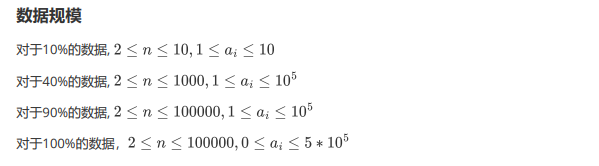
(在考试的时候读错题了没写暴力 555)。
这道题考了思维难度兼代码能力,算是一道很好的题目。
首先,题目中让至少有 n−2n-2n−2 个 iii 满足 ai−ai−1=da_i-a_{i-1}=dai−ai−1=d(其中 ddd 是一个定值),换而言之,就是最多有 222 个 iii 满足 ai−ai−1≠da_i-a_{i-1}\not=dai−ai−1=d,首先 i=1i=1i=1 时肯定是一个,另一个就只能在数列中找了。
因此我们可以把题意稍稍转化一下:在 a1,a2,…,ana_1,a_2,\dots,a_na1,a2,…,an 中找到一个分割点 mmm,使得 ∀i∈[2,m],ai−ai−1=d\forall i\isin[2,m],a_i-a_{i-1}=d∀i∈[2,m],ai−ai−1=d 且 ∀i∈[m+2,n],ai−ai−1=d\forall i\isin[m+2,n],a_i-a_{i-1}=d∀i∈[m+2,n],ai−ai−1=d,为了达到这个目标,我们可以使用两种操作:……
我们现在看其中一个等差数列,比如说 a1∼ama_1\sim a_ma1∼am 这一段吧,假设等差数列的首项是 xxx,那么这个等差数列应该长这样:
x,x+d,x+2d,…,x+(m−1)d x,x+d,x+2d,\dots,x+(m-1)d x,x+d,x+2d,…,x+(m−1)d
对应着:
a1,a2,a3,…,am a_1,a_2,a_3,\dots,a_m a1,a2,a3,…,am
每一个数与要达到的目标相差:
∣a1−x∣,∣a2−x−d∣,∣a3−x−2d∣,…,∣am−x−(m−1)d∣ \mid a_1-x\mid,\mid a_2-x-d\mid,\mid a_3-x-2d\mid,\dots,\mid a_m-x-(m-1)d\mid ∣a1−x∣,∣a2−x−d∣,∣a3−x−2d∣,…,∣am−x−(m−1)d∣
我们把 aaa 和 ddd 放一起,就成了:
∣(a1−0⋅d)−x∣,∣(a2−1⋅d)−x∣,∣(a3−2⋅d)−x∣,…,∣(am−(m−1)⋅d)−x∣ \mid(a_1-0\cdot d)-x\mid,\mid(a_2-1\cdot d)-x\mid,\mid(a_3-2\cdot d)-x\mid,\dots,\mid(a_m-(m-1)\cdot d)-x\mid ∣(a1−0⋅d)−x∣,∣(a2−1⋅d)−x∣,∣(a3−2⋅d)−x∣,…,∣(am−(m−1)⋅d)−x∣
我们现在设 bi=ai−(i−1)db_i=a_i-(i-1)dbi=ai−(i−1)d,那么上面的式子就可以被我们表示成这样:
∣b1−x∣,∣b2−x∣,∣b3−x∣,…,∣bm−x∣ \mid b_1-x\mid,\mid b_2-x\mid,\mid b_3-x\mid,\dots,\mid b_m-x\mid ∣b1−x∣,∣b2−x∣,∣b3−x∣,…,∣bm−x∣
我们所需要的代价就是:
∑bi<x(⌈∣bi−x∣2⌉+[∃k∈Z,∣bi−x∣=2k+1])+∑bi>x∣bi−x∣ \sum_{b_i\lt x}(\lceil\cfrac{\mid b_i-x\mid}{2}\rceil+[\exists k\isin\Z,\mid b_i-x\mid=2k+1])+\sum_{b_i\gt x}\mid b_i-x\mid bi<x∑(⌈2∣bi−x∣⌉+[∃k∈Z,∣bi−x∣=2k+1])+bi>x∑∣bi−x∣
当然这是从题的层面来讲的答案,从数学角度来讲应该长这样:
∑bi<x∣bi−x∣2+∑bi>x∣bi−x∣ \sum_{b_i\lt x}\cfrac{\mid b_i-x\mid}{2}+\sum_{b_i\gt x}\mid b_i-x\mid bi<x∑2∣bi−x∣+bi>x∑∣bi−x∣
我们很容易发现:这不就是要带权的绝对值式最小吗?一般解法是按照零点排序后,取权值的前缀和正好大于等于权值总和的一半时的值最大,这里我们可以直接用结论:取 bm−⌈m3⌉+1b_{m-\lceil\frac{m}{3}\rceil+1}bm−⌈3m⌉+1 或 bm−⌈m3⌉b_{m-\lceil\frac{m}{3}\rceil}bm−⌈3m⌉ 左右时最小(有可能因为括号里面的判断要减一)。
于是我们就找到了 xxx 的值,然后就可以带进公式里算了……吗?
如果我们直接暴力算的话,外面枚举断点,里面再 O(n)O(n)O(n) 的算一下,不直接凉凉了吗?因此对于上面的公式,我们需要转化一下,这里我直接给出结论:
∑bi<x(⌈∣bi−x∣2⌉+[∃k∈Z,∣bi−x∣=2k+1])+∑bi>x∣bi−x∣=∑bi<x⌈∣bi−x∣2⌉+∑bi>x∣bi−x∣+∑bi<x[∃k∈Z,∣bi−x∣=2k+1] \begin{aligned} &\sum_{b_i\lt x}(\lceil\cfrac{\mid b_i-x\mid}{2}\rceil+[\exists k\isin\Z,\mid b_i-x\mid=2k+1])+\sum_{b_i\gt x}\mid b_i-x\mid \\ =&\sum_{b_i\lt x}\lceil\cfrac{\mid b_i-x\mid}{2}\rceil+\sum_{b_i\gt x}\mid b_i-x\mid+\sum_{b_i\lt x}[\exists k\isin\Z,\mid b_i-x\mid=2k+1] \end{aligned} =bi<x∑(⌈2∣bi−x∣⌉+[∃k∈Z,∣bi−x∣=2k+1])+bi>x∑∣bi−x∣bi<x∑⌈2∣bi−x∣⌉+bi>x∑∣bi−x∣+bi<x∑[∃k∈Z,∣bi−x∣=2k+1]
然后分 xxx 的奇偶讨论:
当 xxx 为奇数时:
∑bi<x ∧ ∃k∈Z,bi=2k+1x−bi2+∑bi<x ∧ ∃k∈Z,bi=2k⌈x−bi2⌉+∑bi>x(bi−x)+∑bi<x[∃k∈Z,bi=2k]=x⋅n1−s12+⌊x⋅n0−s02⌋+⌈n02⌉+s−s0−s1−x⋅(s−s0−s1)+n0 \begin{aligned} &\sum_{b_i\lt x\ \land\ \exists k\isin\Z,b_i=2k+1}\cfrac{x-b_i}{2}+\sum_{b_i\lt x\ \land\ \exists k\isin\Z,b_i=2k}\lceil\cfrac{x-b_i}{2}\rceil+\sum_{b_i\gt x}(b_i-x)+\sum_{b_i\lt x}[\exists k\isin\Z,b_i=2k] \\ =&\cfrac{x\cdot n1-s1}{2}+\lfloor\cfrac{x\cdot n0-s0}{2}\rfloor+\lceil\cfrac{n0}{2}\rceil+s-s0-s1-x\cdot(s-s0-s1)+n0 \end{aligned} =bi<x ∧ ∃k∈Z,bi=2k+1∑2x−bi+bi<x ∧ ∃k∈Z,bi=2k∑⌈2x−bi⌉+bi>x∑(bi−x)+bi<x∑[∃k∈Z,bi=2k]2x⋅n1−s1+⌊2x⋅n0−s0⌋+⌈2n0⌉+s−s0−s1−x⋅(s−s0−s1)+n0
当 nnn 为奇数时:
∑bi<x ∧ ∃k∈Z,bi=2kx−bi2+∑bi<x ∧ ∃k∈Z,bi=2k+1⌈x−bi2⌉+∑bi>x(bi−x)+∑bi<x[∃k∈Z,bi=2k+1]=x⋅n0−s02+⌊x⋅n1−s12⌋+⌈n12⌉+s−s0−s1−x⋅(s−s0−s1)+n1 \begin{aligned} &\sum_{b_i\lt x\ \land\ \exists k\isin\Z,b_i=2k}\cfrac{x-b_i}{2}+\sum_{b_i\lt x\ \land\ \exists k\isin\Z,b_i=2k+1}\lceil\cfrac{x-b_i}{2}\rceil+\sum_{b_i\gt x}(b_i-x)+\sum_{b_i\lt x}[\exists k\isin\Z,b_i=2k+1] \\ =&\cfrac{x\cdot n0-s0}{2}+\lfloor\cfrac{x\cdot n1-s1}{2}\rfloor+\lceil\cfrac{n1}{2}\rceil+s-s0-s1-x\cdot(s-s0-s1)+n1 \end{aligned} =bi<x ∧ ∃k∈Z,bi=2k∑2x−bi+bi<x ∧ ∃k∈Z,bi=2k+1∑⌈2x−bi⌉+bi>x∑(bi−x)+bi<x∑[∃k∈Z,bi=2k+1]2x⋅n0−s0+⌊2x⋅n1−s1⌋+⌈2n1⌉+s−s0−s1−x⋅(s−s0−s1)+n1
其中,n0,s0,n1,s1,n,sn0,s0,n1,s1,n,sn0,s0,n1,s1,n,s 分别表示所有的 bi<xb_i\lt xbi<x 中 bib_ibi 是偶数的个数、是偶数的总和、是奇数的个数、是奇数的总和、当前所有数的个数、当前所有数的总和。
这里的相关证明由读者自行推导。
最后一个问题:ddd 怎么确定?很简单,我们可以通过粗略的估计得出这个不等式:
x⋅n+n(n+1)2×d−∑i=1nai2≤amax×n−∑i=1nai2+2n \cfrac{x\cdot n+\cfrac{n(n+1)}{2}\times d-\sum_{i=1}^na_i}{2}\le\cfrac{a_{max}\times n-\sum_{i=1}^na_i}{2}+2n 2x⋅n+2n(n+1)×d−∑i=1nai≤2amax×n−∑i=1nai+2n
即我们的真实答案一定小于等于最大答案。
然后再通过一通粗略的估算我们可以得出这个结论:
∀d,∣d∣≤2×106n \forall d,\mid d\mid\le\cfrac{2\times10^6}{n} ∀d,∣d∣≤n2×106
当然,这不是 ddd 的上界,只是它一定满足这个不等式而已。
因此我们可以先枚举 ddd,里面枚举断点,然后那个大约三分之二的位置可以用线段树(常数略大)或对顶堆来维护,时间复杂度:O(2×106nnlogn)=O(2×106logn)O(\frac{2\times10^6}{n}n\log n)=O(2\times10^6\log n)O(n2×106nlogn)=O(2×106logn),可过。
然后就是代码实现的问题了。
当然,就算你用的是对顶堆,一样需要卡常(我试过,不卡是真的过不去),所以想写线段树的我还真不能保证你能过。
代码(对顶堆):
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
struct seq{
priority_queue<int>pq1;
priority_queue<int,vector<int>,greater<int>>pq2;
int cnt1=0,sum1=0,cnt0=0,sum0=0,sum=0,cnt=0;
__attribute__((always_inline)) void clear()//卡常小技巧:强制内联
{
pq1=priority_queue<int>();//卡常小技巧:直接赋值为空
pq2=priority_queue<int,vector<int>,greater<int>>();
cnt1=sum1=cnt0=sum0=sum=cnt=0;
}
__attribute__((always_inline)) void insert(int x,int y)
{
cnt++,sum+=x;
int len=y-ceil(y*1.0/3);
if(pq1.empty())
{
if(pq2.empty())
{
pq1.push(x);
if(x&1)
{
cnt1++,sum1+=x;
}
else
{
cnt0++,sum0+=x;
}
}
else
{
if(x>pq2.top())
{
pq2.push(x);
}
else
{
pq1.push(x);
if(x&1)
{
cnt1++,sum1+=x;
}
else
{
cnt0++,sum0+=x;
}
}
}
}
else if(x<pq1.top())
{
pq1.push(x);
if(x&1)
{
cnt1++,sum1+=x;
}
else
{
cnt0++,sum0+=x;
}
}
else
{
pq2.push(x);
}
while(pq1.size()>len)
{
pq2.push(pq1.top());
if(pq1.top()&1)
{
cnt1--,sum1-=pq1.top();
}
else
{
cnt0--,sum0-=pq1.top();
}
pq1.pop();
}
while(pq1.size()<len&&!pq2.empty())
{
pq1.push(pq2.top());
if(pq2.top()&1)
{
cnt1++,sum1+=pq2.top();
}
else
{
cnt0++,sum0+=pq2.top();
}
pq2.pop();
}
}
__attribute__((always_inline)) int js(int x)const
//卡常小技巧:常函数(常函数在 CPU 里面自动会有优化)
{
const int num1=(x*cnt1-sum1)>>1,num2=(x*cnt0-sum0)>>1,num3=sum-sum0-sum1-x*(cnt-cnt1-cnt0);
const int h=num1+num2+num3;//卡常小技巧:常数优化
return x&1?h+ceil(cnt0*1.0/2)+cnt0:h+ceil(cnt1*1.0/2)+cnt1;
}
__attribute__((always_inline)) int calc()
{
int ans=0x7ffffffff;
if(__builtin_expect(!pq1.empty(),1))//卡常小技巧(我也不知道叫什么)
{
int top=pq1.top();
int t=js(top);
if(t<ans)
{
ans=t;
}
}
if(__builtin_expect(!pq2.empty(),1))
{
int top=pq2.top();
int t1=js(top),t2=js(top-1);
if(t1<ans)
{
ans=js(top);
}
if(t2<ans)
{
ans=t2;
}
}
return ans;
}
}s;
const int M=1e6;
int n,ans=0x7ffffffff,a[100006];
static int b[100006],fr[100006],ba[100006];
inline int read()//快读
{
int z=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')
{
f=-1;
}
c=getchar();
}
while(c>='0'&&c<='9')
{
z=(z<<3)+(z<<1)+(c^48);
c=getchar();
}
return z*f;
}
inline void write(int x)//快写
{
if(x<0)
{
putchar('-');
x=-x;
}
static int top=0,stk[1006];
while(x)
{
stk[++top]=x%10;
x/=10;
}
if(!top)
{
stk[++top]=0;
}
while(top)
{
putchar(char(stk[top--]+48));
}
}
signed main()
{
n=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
}
int t=M/n;
for(int d=-t;d<=t;d++)
{
int c=0;
for(int i=1;i<=n;++i)
{
b[i]=a[i]-c;
c+=d;//用加法规避乘法
}
for(int i=1;i<n;++i)
{
s.insert(b[i],i);
fr[i]=s.calc();
}
s.clear();
s.insert(b[n],1);
for(int i=n-1;i>=1;--i)
{
ba[i]=s.calc();
s.insert(b[i],n-i+1);
}
s.clear();
for(int i=1;i<n;++i)
{
if(fr[i]+ba[i]<ans)//用判断规避 min 函数
{
ans=fr[i]+ba[i];
}
}
}
write(ans);
return 0;
}






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








