MX 模拟赛三总结

哈哈哈，又一次被题面坑坏了……

T1

题面：

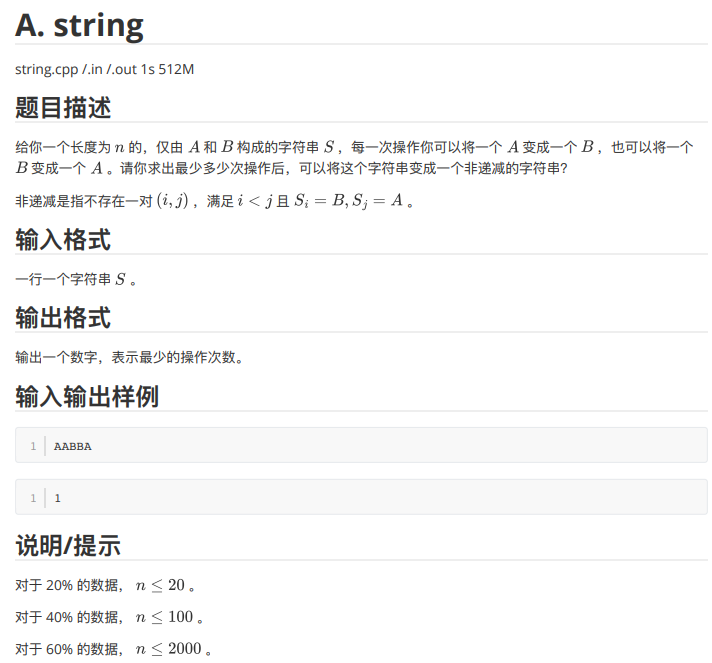
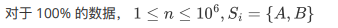
因为要非严格单调递减，所以我们最终的答案肯定是前面一堆 A、后面一堆 B，所以首先前缀和预处理出 A 和 B 的个数，然后暴力枚举从哪划开，然后把前面所有的 B 全变成 A，后面的 A 全变成 B，然后看看什么时候最小就行了。

（代码太简单了，所以我决定不写）。

T2

题面：

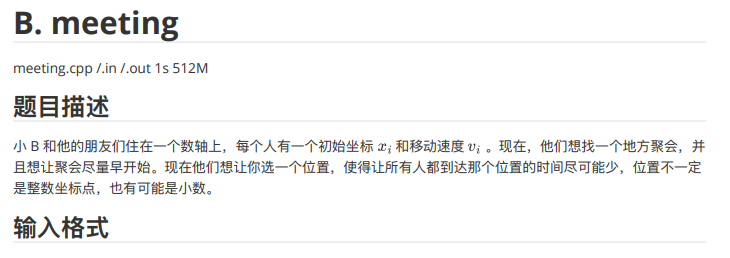
首先这里说一下：题目中让输出的答案是时间，不是地点，但是题目的表述有点小问题（还好我脑子转的快，不然就要被硬控半小时了）。

现在我们来想想怎么做：首先我们变换一下题面，就是“要让时间最长的尽可能的短”，让最大的最小，这不就是二分吗？所以上来很容易想到用二分。

然后就看看 check 函数了呗。目前我们已知运动时间，那很容易求出每个人的运动范围，我们把这些运动范围看成一个个区间，于是原题变成了：已知一些区间，求是否存在一点，使得所有区间都能覆盖到这一点。然后就很好做了，看看左端点的最大值是否小于等于右端点的最小值就行了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const double eps=1e-6;
struct meet{
   
   
	double l,r;
};
int n,mx,x[100006],v[100006];
bool check(double t)
{
   
   
	vector<meet>a(n+6);
	for(int i=1;i<=n;i++)
	{
   
   
		a[i].l=max(0.0,x[i]*1.0-v[i]*1.0*t);
		a[i].r=min(mx*1.0,x[i]*1.0+v[i]*1.0*t);
	}
	double l=0,r=1e7;
	for(int i=1;i<=n;i++)
	{
   
   
		l=max(l,a[i].l);
		r=min(r,a[i].r);
	}
	return l<=r;
}
signed main()
{
   
   
	cin>>n;
	for(int i=1;i<=n;i++)
	{
   
   
		cin>>x[i];
		mx=max(mx,x[i]);
	}
	for(int i=1;i<=n;i++)
	{
   
   
		cin>>v[i];
	}
	double l=0,r=1e7,mid,ans;
	while(r-l>=eps)
	{
   
   
		mid=(l+r)/2;
		if(check(mid))
		{
   
   
			ans=mid;
			r=mid;
		}
		else
		{
   
   
			l=mid;
		}
	}
	printf("%0.5lf",ans);
	return 0;
}

T3

题面：

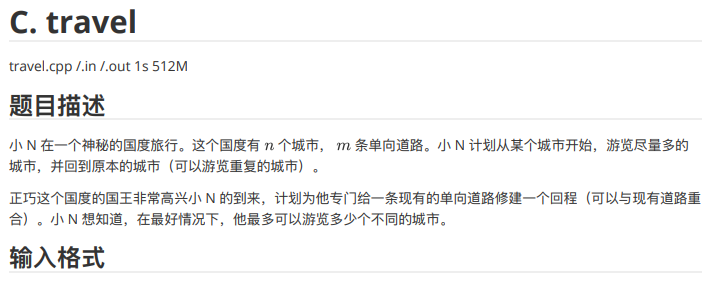
（我想题面大概是有点问题吧，不然我也不会两个半小时没看懂题）。

首先我要解释清楚这里的加边规则：我们只能在原图已有的边上加一条反边。什么意思？意思就是指你不能随便找两个点就连起来，这两个点必须相邻！！！

然后我就被卡在这两个半小时之久……

正解也不难想到：反正边数最多 $4e4$，大不了暴力枚举一下。因此我们可以枚举每一条边，然后在这条边的基础上建反边，然后算一下答案即可。

当然，这里算答案的方式有很多，反正我用的 tarjan，题解给的是用 dfs。

最后说一点：其实在枚举之前你可以先跑一边 tarjan 缩点，因为你在一个 SCC 里面多加一条边是完全没用的，但你如果在两个 SCC 之间多加一条边可就不一样了，所以缩完点之后边数就会减少。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,m,cnt,ti,ans,rd[2006],siz[2006],sizz[2006],dfn[2006],low[2006],bel[2006];
bool ins[2006];
set<int>v[2006];
set<int>g[2006];
stack<int>st;
void tarjan(int x)
{
   
   
	dfn[x]=low[x]=++ti;
	st.push(x);
	ins[x]=1;
	for(auto i:v[x])
	{
   
   
		if(!dfn[i])
		{
   
   
			tarjan(i);
			low[x]=min(low[x],low[i]);
		}
		else if(ins[i])
		{
   
   
			low[x]=min(low[