一篇文章带你领略欧拉公式的美上：自然常数 e

前言

好久没写文章了，今天来更新一下。

最近看了一些和高数有关的书，感觉挺有趣，然后就想着来讲一讲这个欧拉公式 $e^{i\pi }+1=0$，因为这个公式也是有很多好玩的和值得深思的地方，所以今天来跟大家讲一讲。

因为每个符号都有很大的作用，几乎是独占一方天地，因此这个系列会被分成三章来讲。

在读这篇文章之前，建议您先学一下微积分基础，然后再来看，或者说等我后面补一下关于微积分的文章（这里挖个坑啊）。

正片

要想理解这个公式，首先我们要把这个公式拆解开。

0 和 1

在这个公式中，最基础的就是这个 $0$。$0$ 本身的含义是虚无的、不存在的，同时也是所有数字的起点。而 $1$ 则是单位，$1$ 个单位就是 $1$。然后单位的累加就形成了自然数，累减就形成了整数。在数轴上就是向右移和向左移的操作。

这是比较基础的部分，因此我们不细讲。

自然常数 $e$

关于自然常数 $e$ 的定义有很多，比如说 $e={\lim }_{n\to +\infty }(1+\frac{1}{n}{)}^n$、$(e^x{)}^{\prime }=e^x$ 等等。然而 $e$ 最初的定义来自于复利率。

传说有一个银行，年利率是 $100\%$，即你的本金在一年后会翻一倍，当然你可以多次存取，假设你存取了 $n$ 次，那么第一次取出来就会有 $1+\frac{1}{n}$ 倍的钱，再存进去取出来就会有 $(1+\frac{1}{n}{)}^2$ 倍，直到第 $n$ 次，此时的总金额达到了 $(1+\frac{1}{n}{)}^n$，发现没有，这个值其实就是 $e$，大约是 $2.718$。

其实上面这个故事中已经蕴含着 $e^{\prime }=e$ 了，因为 $e$ 每次的增长速度其实就等于本金，因此对 $e$ 求导就是 $e$。

关于 $e$ 还有另一种表示方法，即泰勒展开，我们可以得到 $e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\dots$。

这里说一下泰勒展开：

泰勒展开

定义：对于任意一个在 $a$ 处可无限导的函数，有 $f(x)=f(a)+f^{\prime }(a)\times \frac{(x-a)}{1!}+f^{\prime \prime }(a)\times \frac{(x-a{)}^2}{2!}+\dots$，由于 $e^x$ 求导后就是 $e^x$，所以 $e^x$ 在 $0$ 处可无限导，所以得到 $f(x)=f(0)+f^{\prime }(0)\times x+f^{\prime \prime }(0)\times \frac{x^2}{2!}+\cdots =1+x+\frac{x^2}{2!}+\dots$，然后令 $x=1$ 就可以求出 $e$ 了。

其实关于 $e$ 的泰勒展开，还有另一种求法。

等比数列

我们已知一个数列满足相邻两项的商固定，请问这个数列的前 $n$ 项的和是多少？

我们可以转化成这样一个问题：

$$\sum _{i=0}^n{a}_1\cdot x^i$$

对于这种问题，我们在初中的时候就学过一种方法：

设 $S={\sum }_{i=0}^n{a}_1\cdot x^i=a_1+a_1\cdot x+\cdots +a_1\cdot x^n$，则：

$$\therefore xS=a_1\cdot x+a_1\cdot x^2+\cdots +a_1\cdot x^{n+1}$$

$$\therefore (x-1)S=a_1\cdot x^{n+1}-a_1$$

$$\therefore S=a_1\cdot \frac{x^{n+1}-1}{x-1}$$

于是我们就用巧妙的方法求出了它的和。

现在我们考虑这样一个问题：当 $n$ 趋向于无穷，且 $x<1$，这时候 $S$ 又是多少？

这个问题也不难解决，用一点点数学常识就可以知道：因为 $x<1$，所以整个数列是收敛的，最终一定会等于一个确定的值，这个值就是下面这个式子：

$$\underset{n\to +\infty }{\lim }{a}_1\cdot \frac{x^{n+1}-1}{x-1}=\frac{a_1}{1-x}$$

从特殊到一般

我们来想一个更抽象的问题：有没有可能这个 $x$ 不是一个数，而是一种操作，且在无限次操作下最后这个值会收敛到一个确定的值？

我们还是回到这个式子上来：除号我们可以写作 $-1$ 次幂的运算，然后 $1$ 和 $x$ 我们看做初始状态和每次的操作（这里分别设为 $I$ 和 $P$），于是原式就被我们变成了这样：

$$a_1\cdot (I-P{)}^{-1}$$

放在操作的角度来看：就是从初始状态做了一次操作的逆操作。那这个式子是否正确呢？

我们举个小例子：就拿向量旋转说吧。假定有一个初始向量 $\vec{a}=\left(\begin{array}{c}1\\ 0\end{array}\right)$（上面是横坐标，下面是纵坐标），我要让它逆时针旋转 $45^{\circ }$，再把模长缩小到原来的 $\frac{\sqrt{2}}{2}$ 倍，把这个操作写成矩阵就是：

$$\begin{array}{rl}& \frac{\sqrt{2}}{2}\left(\begin{array}{c}\cos 45^{\circ }-\sin 45^{\circ }\\ \sin 45^{\circ }\cos 45^{\circ }\end{array}\right)\\ =& \frac{\sqrt{2}}{2}\left(\begin{array}{c}\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}\end{array}\right)\\ =& \left(\begin{array}{c}\frac{1}{2}-\frac{1}{2}\\ \frac{1}{2}\frac{1}{2}\end{array}\right)\end{array}$$

我们来测试一下：

$$\left(\begin{array}{c}\frac{1}{2}-\frac{1}{2}\\ \frac{1}{2}\frac{1}{2}\end{array}\right)\times \left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}\frac{1}{2}\\ \frac{1}{2}\end{array}\right)$$

位置是对的，应该没有问题。

现在我们设这个操作 $P=\left(\begin{array}{c}\frac{1}{2}-\frac{1}{2}\\ \frac{1}{2}\frac{1}{2}\end{array}\right)$，那么实际上我们的等比数列求和就成了无限多个向量求和，见下图：

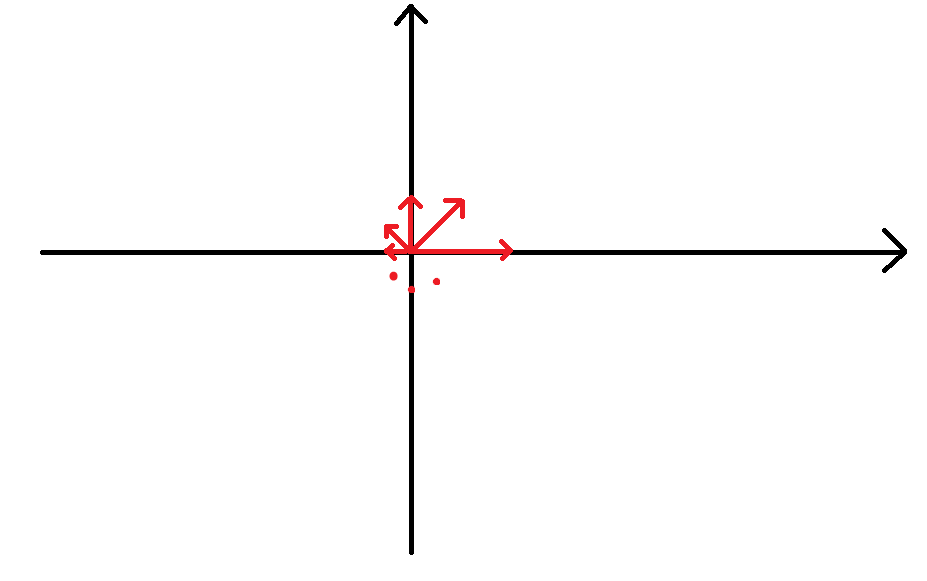
即把原向量每次按照上面的操作操作无线次后得到的向量。

然后利用向量加法的规则，我们把这些向量首尾拼在一起：

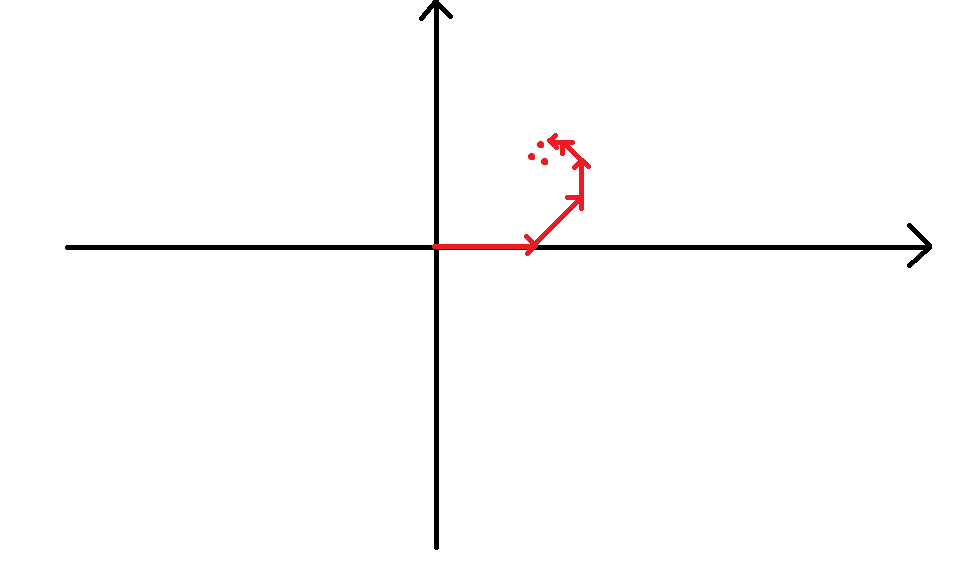
你会发现它们最后收敛到一个确定的位置。

现在我们尝试使用我们的公式：进行一次原操作的逆操作。

我们来分析一波原本的操作：对于一个与横轴形成 $45^{\circ }$ 角的向量，它进行一次这个操作就相当于在纵轴上做了它的投影：

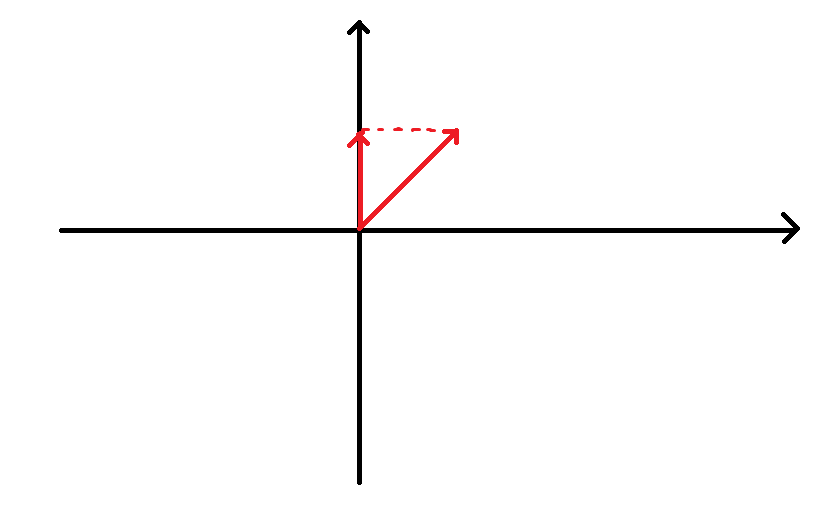
于是我们可以标出 $I$ 和 $P$：

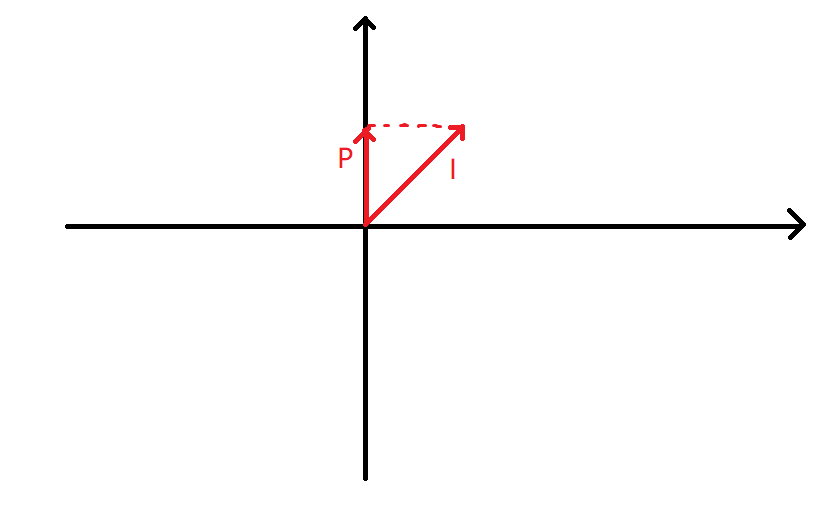
那根据向量减法，上面那一个向量应该就是 $I-P$：

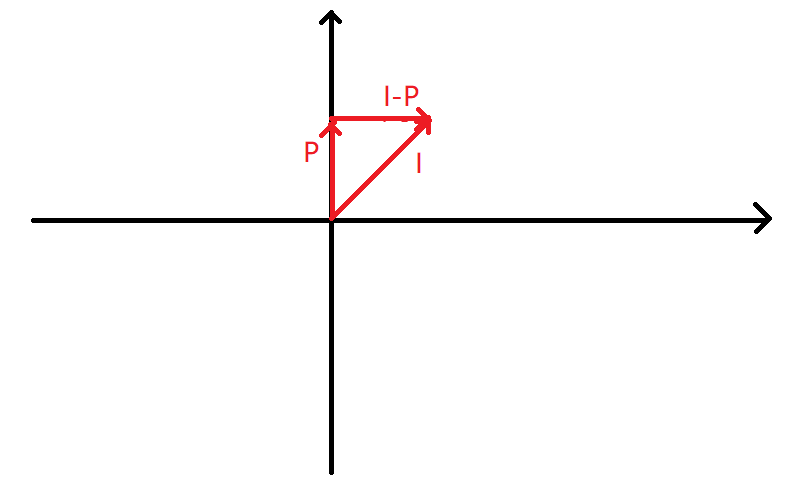
移到坐标轴上：

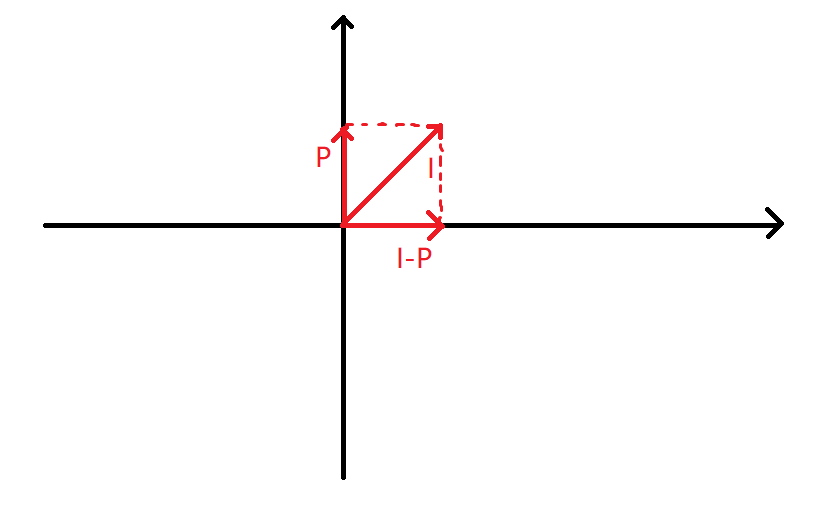
所以 $(I-P)$ 这个操作就相当于原向量顺时针旋转 $45^{\circ }$，再把原长度缩小到原来的 $\frac{\sqrt{2}}{2}$ 倍。那它的逆操作就是把原向量逆时针旋转 $45^{\circ }$，再把长度变为原来的 $\sqrt{2}$ 倍，我们来实际操作一下：

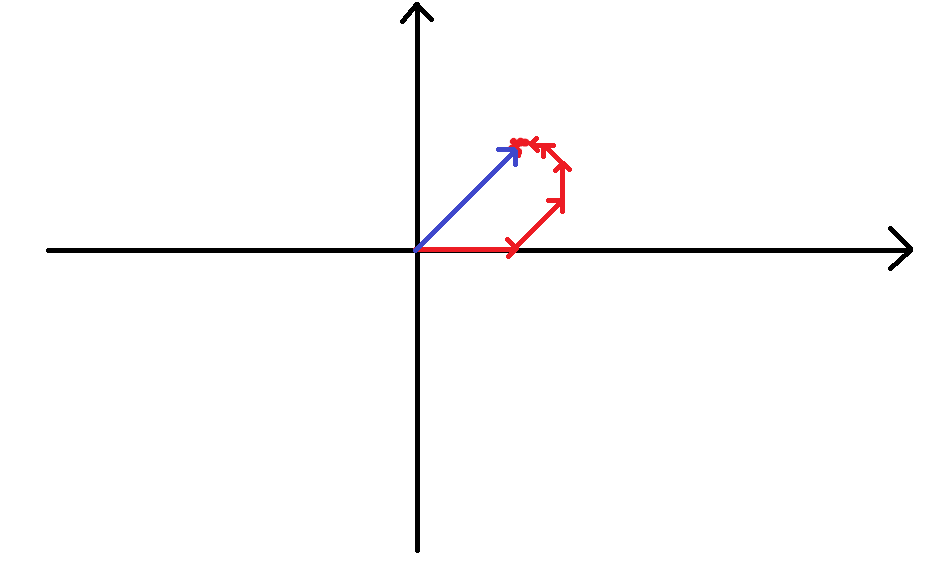
图稍微有点简陋，但是可以保证这两个的终点指向的是同一个地方！

因此我们验证了 $a_1(I-P{)}^{-1}$ 是一个完全可行的方法。

逆向使用

其实对于那个求和式子，我们还可以逆向使用它：$a_1(I-P{)}^{-1}=I{a}_1+P{a}_1+P^2{a}_1+P^3{a}_1+\dots$。

现在回到求 $e$ 这个问题上来。我们知道自然常数 $e$ 满足这个式子：

$$(e^x{)}^{\prime }=e^x$$

因此它也就满足这个式子：

$$\int e^x=e^x$$

我们现在把积分看做一个操作，那么：

$$\begin{array}{rl}{e}^x-\int e^x& =0\\ (1-\int )\cdot e^x& =0\\ e^x& =0\cdot (1-\int {)}^{-1}\end{array}$$

（有点奇葩，但是真的可以这么干）。

然后把右边展开：

$$\begin{array}{rl}{e}^x& =0\cdot 1+\int 0+\int \int 0+\int \int \int 0+\dots \\ & =0+1+x+\frac{x^2}{2}+\frac{x^3}{2\cdot 3}+\dots \\ & =\sum _{i=0}^{\infty }\frac{x^i}{i!}\end{array}$$

这其实就是 $e^x$ 的泰勒展开。

总结一下

从一个很奇葩的假想问题，到一个真实的定义，自然常数 $e$ 总是会在你想不到的地方出现。而且，$e^x$ 积分后等于自己这种良好的性质也让我们领略到了从特殊到一般的思维历程，体会到了数学中的抽象思维。而且，当你把 $e$ 和 $i$ 放在一起的时候，它们又会给千千万万的数学家、物理学家带来意想不到的方便。到底方便在哪儿呢？

敬请期待下一章：《一篇文章带你领略欧拉公式的美中：虚数单位 i》。