CSP-S 模拟赛十一总结-优快云博客

T1

题面：

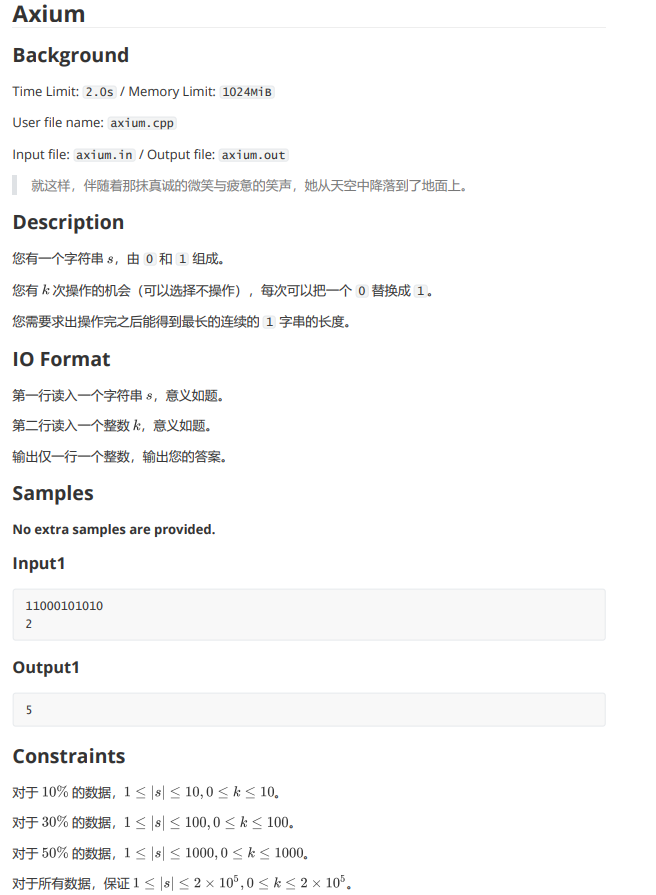
特别水的一道题。

你只需要枚举一下起点，然后看看最远能延伸到哪，然后算一下个数就行了。

代码自己写。

T2

题面：

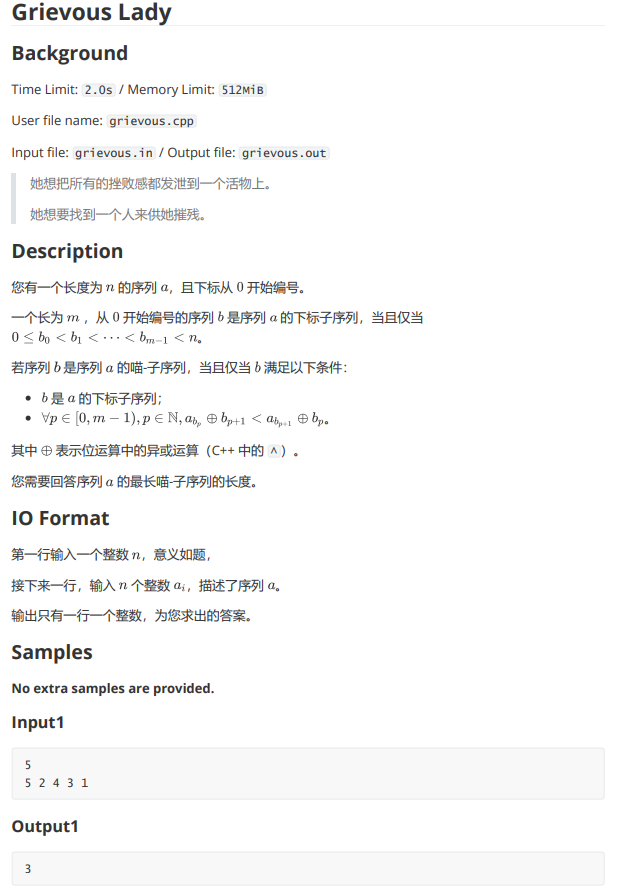
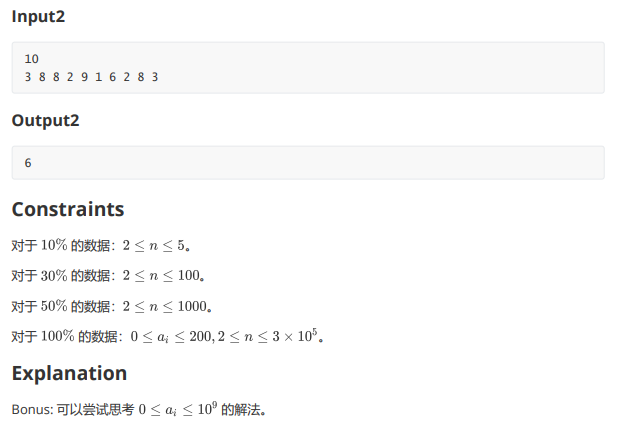
题目上的约束条件转化一下实际上就是要求一个最长的子序列满足相邻两项中前一项的值与后一项的下标的异或值要小于后一项的值与前一项的下标的异或值。对于这种题，不难想打用 DP 来解决。

因此我们设 $f_i$ 表示以第 $i$ 个数为结尾能组成的最长的满足条件的子序列。于是我们可以写出一个暴力转移：

for(int i=0;i<n;i++)
{
	f[i]=1;
	for(int j=0;j<i;j++)
	{
		if((a[i]^j)>(a[j]^i))
		{
			f[i]=max(f[i],f[j]+1);
		}
	}
}

但是我们会发现这个的时间复杂度是 $O(n^2)$ 的，明显只有 50pts。因此考虑优化。

看到二进制下的运算，不难想到把 $i$ 和 $a_i$ 都变成二进制，我们来看看二进制下有什么特点。

因为 $ai≤200a_i\le200$ ，所以 $a_i$ 在二进制下最多 $8$ 位，也就是说 $ai⊕ja_i\oplus j$ 最多只会改变 $j$ 的后八位，而前面的一直不变，所以如果 $j$ 在二进制下的前面几位就已经小于 $i$ 的前几位了，那 $ai⊕ja_i\oplus j$ 就一定小于 $aj⊕ia_j\oplus i$ 了，因此 $j$ 的范围实际上只有 $256,i][i-i\bmod256,i]$ 这个区间，然后枚举一下就行了。

时间复杂度： $O (256 n)$ 。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,a[300006],f[300006];
signed main()
{
//	freopen("grievous.in","r",stdin);
//	freopen("grievous.out","w",stdout);
	cin>>n;
	for(int i=0;i<n;i++)
	{
		cin>>a[i];
	}
	for(int i=0;i<n;i++)
	{
		f[i]=1;
		int k=i-(i&255);
		for(int j=0;j<256&&j+k<i;j++)
		{
			if((a[i]^(j+k))>(a[j+k]^i))
			{
				f[i]=max(f[i],f[j+k]+1);
			}
		}
	}
	int ans=0;
	for(int i=0;i<n;i++)
	{
		ans=max(ans,f[i]);
	}
	cout<<ans;
	return 0;
}

T3

题面：

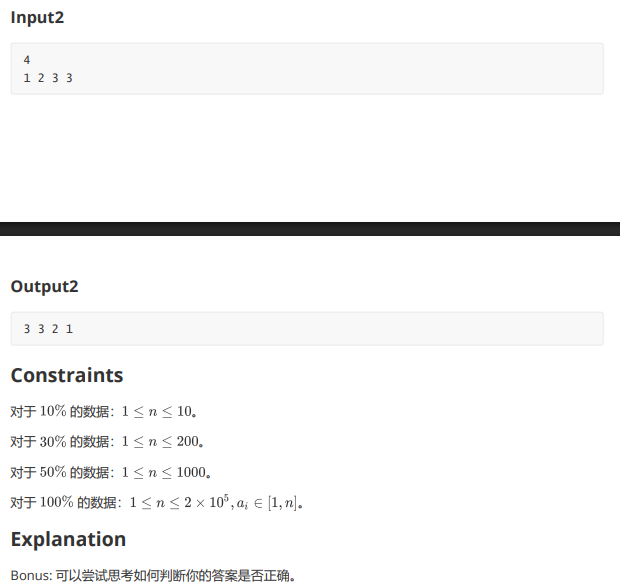
其实我觉得这题挺难的。

首先如果 $a_i=b_j$ ，那么 $i$ 就有可能会到 $j$ 这个位置上去，因此我们可以从 $a_i$ 向 $b_j$ 连边（若有相同的 $a_i$ 按不同的点算）。因为每个数只能变成一个数，又只能被一个数变成，所以每个点只会有一个入读、一个出度，所以最终整张图一定会变成很多个环。

现在让我们来证明一些结论：

结论一：把一个环上的任意两个点所能到达的点交换后，这个环会变成两个环。
证明：若一个环是按照 $g1→g2→g3→⋯→gm→g1g_1\to g_2\to g_3\to\dots\to g_m\to g_1$ 的顺序构成的，如果被交换的是 $i$ 和 $j$ （ $i<ji\lt j$ ），那么原本的环就会变成这样： $g1→g2→g3→⋯→gi−1→gj→⋯→gm→g1g_1\to g_2\to g_3\to\dots\to g_{i-1}\to g_j\to\dots\to g_m\to g_1$ 和 $gi→gi+1→⋯→gj−1→gig_i\to g_{i+1}\to\dots\to g_{j-1}\to g_i$ 。
结论二：把两个环上的任意两点所能到达的点交换后，这两个环会合并成一个环。
证明：若这两个环是 $g1→g2→⋯→gm→g1g_1\to g_2\to\dots\to g_m\to g_1$ 和 $h1→h2→⋯→hk→h1h_1\to h_2\to\dots\to h_k\to h_1$ ，若把 $g_i$ 和 $h_j$ 交换了，那么原图就会变成这样： $g1→g2→⋯→gi−1→hj→hj+1→⋯→hj−1→gi→gi+1→⋯→gm→g1g_1\to g_2\to\dots\to g_{i-1}\to h_j\to h_{j+1}\to\dots\to h_{j-1}\to g_i\to g_{i+1}\to\dots\to g_m\to g_1$ 。
结论三：一个环上的所有点要到正确的位置的最小交换次数是环长减一。
证明：使用数学归纳法证明。
设 $F (G)$ 表示一个环 $G$ 上所有点要到正确位置的最小交换次数， $S (G)$ 表示环 $G$ 的环长。
显然当 $S (G) = 1$ 时， $F (G) = 0$ ， $S (G) = 2$ 时， $F (G) = 1$ 。
若对于 $∀S(G)≤k\forall S(G)\le k$ ， $F (G) = S (G) - 1$ ，则当 $S (G) = k + 1$ 时，显然可以通过交换环上的两个点把原本的环变成两个小环 $G_1,G_2$ ，明显 $S(G1),S(G2)<S(G),S(G1)+S(G2)=S(G)S(G_1),S(G_2)\lt S(G),S(G_1)+S(G_2)=S(G)$ ，所以 $F(G_1)=S(G_1)-1,F(G_2)=S(G_2)-1$ ，所以 $F(G)=F(G_1)+F(G_2)+1=S(G)-1$ （加一是加上拆环时交换的那一步），因此得证。
结论四：若一张图的节点数为 $S (G)$ ，环的数量为 $N (G)$ ，则这张图上所有点回到正确位置的最小交换次数为 $S (G) - N (G)$ 。
证明：由结论三可知：每个环 $G_i$ 的最小交换次数是 $S(G_i)-1$ ，因此总的最小交换次数就是 $∑S(Gi)−1=S(G)−N(G)\sum S(G_i)-1=S(G)-N(G)$ ，得证。

知道结论四后，这道题就非常好做了。因为我们要最小交换次数最大化，所以就是要这张图内的环的个数尽可能的少。因为相同的数不会放在同一个环上，所以我们只需要把那些不相同的数尽可能的放在同一个环上就行了。

要放在同一个环上，我们只需要让这些数都错位而且正好能形成一个环就行了，那最简单的方法就是让第一个数换到最后一个位置上，然后其他数都往前挪一个单位，这样正好能形成一个环。

然后代码就很好写了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,a[200006],cnt[200006];
vector<int>v[200006];
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		v[++cnt[a[i]]].push_back(i);
	}
	for(int i=1;i<=n;i++)
	{
		sort(v[i].begin(),v[i].end(),[&](int x,int y)
		{
			return a[x]<a[y];
		});
		for(int j=1;j<v[i].size();j++)
		{
			swap(a[v[i][j-1]],a[v[i][j]]);
		}
	}
	for(int i=1;i<=n;i++)
	{
		cout<<a[i]<<" ";
	}
	return 0;
}

T4

题面：

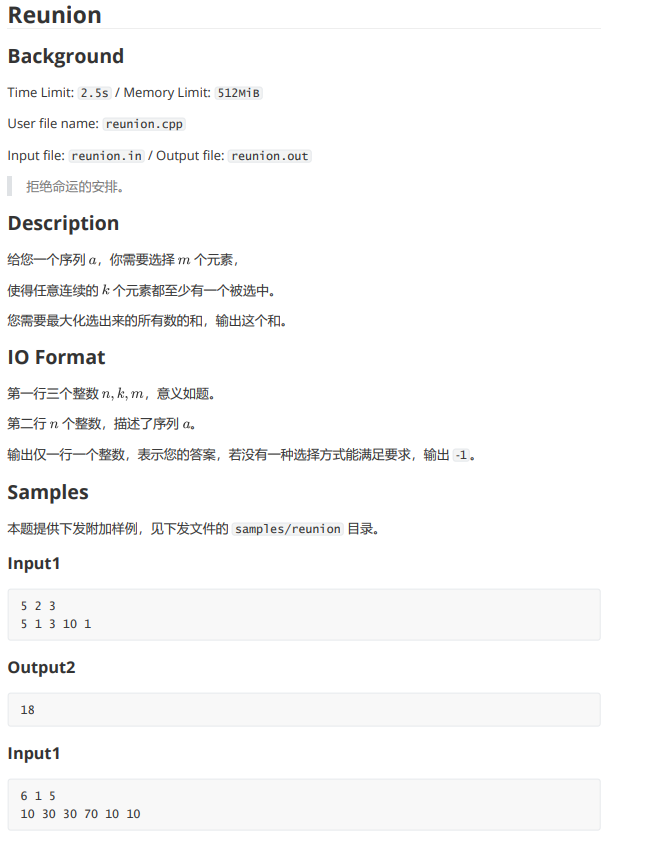
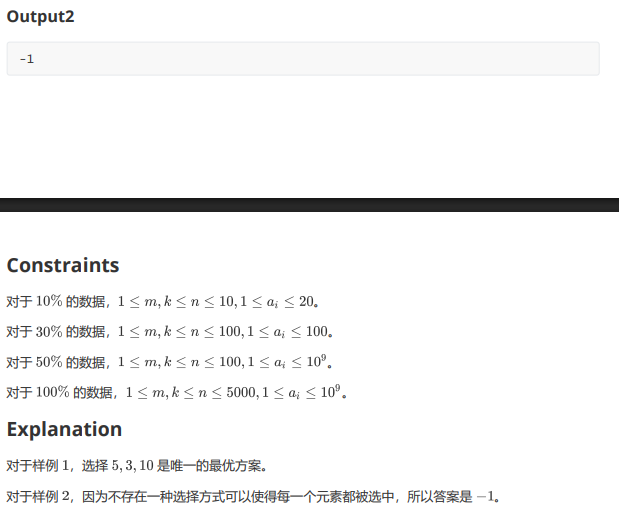
这题其实比 T2 还好想。

首先看到这种题明显设 DP。设 $f_{i,j}$ 表示前 $i$ 个中选了 $j$ 个切满足条件的最大总和。

你可以试着转移一下这个 DP，但是你很快就会发现这个 DP 没法转移，因为你不知道当前这个点有没有被选过，这时有两种方案：

增加限制条件。
增加定义的维度。

我选的是第二种方法：设 $f_{0/1,i,j}$ 表示前 $i$ 个中选了 $j$ 个且当前点没被选过/被选过的最大总和。于是你就能很愉快的转移这个 DP 了：

$f_{1,i,j}=\max\{f_{0,i-1,j-1},f_{1,i-1,j-1}\}+a_i \\ f_{0,i,j}=\max_{l=\max\{1,i-k+1\}}^{i-1}\{f_{1,l,j}\}$

写出来你会发现时间复杂度是 $O(nk^2)$ 的，明显过不了。

仔细观察第二个转移方程，你会发现里面的那一块其实是一个滑动窗口！所以使用滑动窗口优化 DP，时间复杂度 $O (nk)$ 。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,k,m,a[5006],f[2][5006][5006];
deque<int>dq[5006];
signed main()
{
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	if(k*((m-1)*2+1)<n)
	{
		cout<<-1;
		return 0;
	}
	memset(f,-0x3f,sizeof(f));
	f[0][0][0]=0;
	for(int i=1;i<=n;i++)
	{
		if(i<m)f[0][i][0]=0;
		for(int j=1;j<=min(k,i);j++)
		{
			f[1][i][j]=max({f[1][i][j],f[1][i-1][j-1]+a[i],f[0][i-1][j-1]+a[i]});
			while(!dq[j].empty()&&dq[j].front()<max(1ll,i-m+1))
			{
				dq[j].pop_front();
			}
			if(!dq[j].empty())
			{
				f[0][i][j]=max(f[0][i][j],f[1][dq[j].front()][j]);
			}
			while(!dq[j].empty()&&f[1][dq[j].back()][j]<f[1][i][j])
			{
				dq[j].pop_back();
			}
			dq[j].push_back(i);
		}
	}
	cout<<max(f[0][n][k],f[1][n][k]);
	return 0;
}