T1
题面:

首先讲一个很简单的做法,同学们打开 OI-wiki,然后找到 DP 那一章中的《状态设计优化》那一章,然后看到第一道例题。
链接直达:https://oi-wiki.org/dp/opt/state/。
然后这题就做完了……
(好吧其实我也是后面才知道这件事的)。
言归正传,我们来讲一下思路。
首先这种题最基础的做法就是 O ( n m ) O(nm) O(nm) 暴力 DP 求 LCS(如果这都不会建议回炉重造一遍),当然这种方案放在这题肯定是不行的。
我们仔细观察,不难发现 B B B 的长度很小,而我们知道两个字符串的 LCS 的长度一定是小于等于两个字符串中最小长度的,因此我们可以有一个大胆的想法:先枚举一次 B B B,然后枚举 LCS 的长度。
因此我们的 DP 可以换一种设计方法:设 f i f_i fi 表示 LCS 长度为 i i i 时在 A A A 中对应的位置(你也可以设计成是否存在,但是这样的话不方便后面转移)。但是这个位置很多,我们只能找一个位置。
这时我突然想起之前做的有一道题,里面的 DP 具有贪心性,即它选最靠前的那个位置就一定是最优解,我突发奇想:这题的 DP 是不是也具有贪心性呢?
具体证明我就不在这里多说了,反正最后能证明出来选最靠前的位置一定是最优的。
然后我们就可以愉快的写代码了:只要找到下一个能接上的位置转移 DP 就行了(这个 DP 还是很好转移的吧)。至于这个位置,你可以选择预处理( O ( 26 n + m 2 ) O(26n+m^2) O(26n+m2))或者二分( O ( m 2 log m ) O(m^2\log m) O(m2logm))。
代码(二分):
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n1,n2,f[1006],s[26][1000006];
string s1,s2;
signed main()
{
cin>>s1>>s2;
n1=s1.size();
n2=s2.size();
s1=" "+s1;
s2=" "+s2;
for(int i=1;i<=n2;i++)
{
f[i]=1e18;
}
for(int i=1;i<=n1;i++)
{
for(int j=0;j<26;j++)
{
s[j][i]+=s[j][i-1];
}
s[s1[i]-'a'][i]++;
}
f[0]=0;
for(int i=1;i<=n2;i++)
{
for(int j=i;j>=1;j--)
{
if(f[j-1]!=1e18)
{
int it=lower_bound(s[s2[i]-'a']+f[j-1]+1,s[s2[i]-'a']+n1+1,s[s2[i]-'a'][f[j-1]]+1)-s[s2[i]-'a'];
//从当前位置开始往后找下一个能接上的位置
f[j]=min(f[j],(it>n1?(int)1e18:it));//转移 DP
}
}
}
for(int i=n2;i>=0;i--)
{
if(f[i]!=1e18)
{
cout<<i;
break;
}
}
return 0;
}
T2
题面:



首先我们很容易想到要找到最小环的长度,相当于要找到一个环,这个找环的方法很多,我在这里说一种。
我们钦定一个起点,然后从这个起点开始扫,同时设一个 d i s dis dis 数组,表示每个点到起点的距离,然后就会出现类似于 tarjan 的思想:如果说你找到了一个距离比你远的点,说明这个点之前已经通过别的边来过了,因此这里就可以形成一个环,环长就是当前点的距离加上它要到的那个点的距离再加一(当前边)。
现在我们就可以开始找环的个数了,我们用一种类似于分割的思想:
如果一个环长为 l e n len len,从起点开始走一步能走的路径有 x x x 条,走 l e n − 1 len-1 len−1 步能走的路径有 y y y 条,那么总共就有 x ⋅ y x\cdot y x⋅y 个这样的环。
结合这个思想,我们可以采用这样一种方法:对于一个环,我们可以看看当中长度为 ⌊ l e n 2 ⌋ \lfloor\frac{len}{2}\rfloor ⌊2len⌋ 的路径有多少条,然后互相搭配,就可以得到这种环的个数。
当然为了方便,我们可以每到一次长度为 ⌊ l e n 2 ⌋ \lfloor\frac{len}{2}\rfloor ⌊2len⌋ 的点就加上一次路径条数。这时我们上面的算法的好处就体现出来了:因为一个环经过上面的操作之后必定能被分成长度几乎相等的两部分,所以最后我们能到的那个点肯定是长度为 ⌊ l e n 2 ⌋ \lfloor\frac{len}{2}\rfloor ⌊2len⌋ 的点。
最后就是一点细枝末节的东西:我们知道一个奇环其实有两个这样的点,因此奇环最终的答案必须要除以 2 2 2,而且我们知道一个偶环左右是一样的,所以在计数后要加上另一侧的路径条数。最终答案由于环上每个点都做了一次起点,所以答案要除以 l e n len len。
没听懂的看代码。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,m,ans,mn=1e18;
vector<int>v[3006];
void bfs1(int st)//求环长
{
queue<int>q;
vector<int>dis(n+6,-1);
dis[st]=0;
q.push(st);
while(!q.empty())
{
int u=q.front();
q.pop();
for(auto i:v[u])
{
if(dis[i]!=-1)
{
if(dis[i]>=dis[u])
{
mn=min(mn,dis[i]+dis[u]+1);
}
continue;
}
q.push(i);
dis[i]=dis[u]+1;
}
}
}
void bfs2(int st)
{
queue<int>q;
vector<int>dis(n+6,-1),cnt(n+6,0);
dis[st]=0;
cnt[st]=1;
q.push(st);
while(!q.empty())
{
int u=q.front();
q.pop();
for(auto i:v[u])
{
if(dis[i]!=-1)
{
if(dis[i]>=dis[u]&&dis[i]+dis[u]+1==mn)
{
ans+=cnt[i];//统计答案
if(!(mn&1))
//如果是偶环,左右一样,因此和左边或右边结合后都是一个整环
//所以要加上这一侧的路径条数
{
cnt[i]+=cnt[u];
}
}
continue;
}
q.push(i);
dis[i]=dis[u]+1;
cnt[i]=cnt[u];//传递
}
}
}
signed main()
{
cin>>n>>m;
for(int i=1,x,y;i<=m;i++)
{
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
for(int i=1;i<=n;i++)
{
bfs1(i);
}
for(int i=1;i<=n;i++)
{
bfs2(i);
}
if(mn&1)//如果是奇环,因为会有两个点都算了一遍答案,因此要除以二
{
ans/=2;
}
ans/=mn;
cout<<ans;
return 0;
}
T3
题面:


我来一步一步讲一下我是如何想到正解的(当然,最后我们老师把题解发下来了,我是看了题解之后想通的)。
首先我们很容易想到一个非常暴力的 dfs 做法:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353;
int k,q,a,b,ans;
void dfs(int x,int sum,int cnt)
{
if(x>a)
{
if(b*cnt==sum&&cnt&&sum)
{
ans++;
if(ans>=mod)
{
ans-=mod;
}
}
return;
}
for(int i=0;i<=k;i++)
{
dfs(x+1,sum+x*i,cnt+i);
}
}
signed main()
{
cin>>k>>q;
while(q--)
{
cin>>a>>b;
dfs(1,0,0);
cout<<ans<<'\n';
ans=0;
}
return 0;
}
这份代码可以得到 15pts。
当然,你也可以佳航一些奇奇怪怪的东西,让它的分数更高一点。
但是这份代码中的一点给了我一个小灵感:把除法换成乘法。
于是我们可以列出一个我们要满足的式子:
∑ i = 1 n i × c n t i = b × ∑ i = 1 n c n t i \sum_{i=1}^ni\times cnt_i=b\times\sum_{i=1}^ncnt_i i=1∑ni×cnti=b×i=1∑ncnti
然后稍微转化一下:
∑ i = 1 n i × c n t i = ∑ i = 1 n ( c n t i × b ) \sum_{i=1}^ni\times cnt_i=\sum_{i=1}^n(cnt_i\times b) i=1∑ni×cnti=i=1∑n(cnti×b)
接着展开、把右边移到左边:
1 × c n t 1 + 2 × c n t 2 + ⋯ + n × c n t n = b × c n t 1 + b × c n t 2 + ⋯ + b × c n t n ( 1 − b ) × c n t 1 + ( 2 − b ) × c n t 2 + ⋯ + ( n − b ) × c n t n = 0 \begin{aligned} 1\times cnt_1+2\times cnt_2+\dots+n\times cnt_n&=b\times cnt_1+b\times cnt_2+\dots+b\times cnt_n \\ (1-b)\times cnt_1+(2-b)\times cnt_2+\dots+(n-b)\times cnt_n&=0 \end{aligned} 1×cnt1+2×cnt2+⋯+n×cntn(1−b)×cnt1+(2−b)×cnt2+⋯+(n−b)×cntn=b×cnt1+b×cnt2+⋯+b×cntn=0
因此,实际上就是问满足
∑ i = 1 n ( i − b ) × c n t i = 0 \sum_{i=1}^n(i-b)\times cnt_i=0 i=1∑n(i−b)×cnti=0
这个式子的 c n t i cnt_i cnti 有多少种搭配方案。
于是就会有一个很自然的想法:设 f i , j f_{i,j} fi,j 表示考虑前 i i i 个,总和为 j j j 时的方案数,转移如下:
f i , j = f i , j + f i − 1 , j − l × ( i − b ) ( l ∈ [ 0 , k ] ) f_{i,j}=f_{i,j}+f_{i-1,j-l\times(i-b)}(l\isin[0,k]) fi,j=fi,j+fi−1,j−l×(i−b)(l∈[0,k])
代码如下(使用滚动数组加了空间优化):
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353,p=1500000;
int k,q,n,b,a[156],f[2][3000006];
signed main()
{
cin>>k>>q;
while(q--)
{
memset(f,0,sizeof(f));
cin>>n>>b;
for(int i=1;i<=n;i++)
{
a[i]=b-i;
}
f[0][p]=1;//为了防止负数下标出现,对下标多加了一个 1.5e6
for(int i=1;i<=n;i++)
{
int now=i&1,odd=(i&1)^1;
for(int j=0;j<=3000000;j++)
{
if(!f[odd][j])
{
continue;
}
f[now][j]=(f[now][j]+f[odd][j])%mod;
for(int l=1;l<=k;l++)
{
if(j+l*a[i]<0||j+l*a[i]>3000000)
{
continue;
}
f[now][j+l*a[i]]+=f[odd][j];
f[now][j+l*a[i]]%=mod;
}
f[odd][j]=0;
}
}
cout<<(f[n&1][p]-1+mod)%mod<<'\n';
}
return 0;
}
但是一算时间复杂度,跟上面的 dfs 没什么区别。因此考虑优化。
首先就是第二层循环的范围问题:并不是每次的范围都一定是 [ 0 , 3 × 1 0 6 ] [0,3\times10^6] [0,3×106],从这一点入手,可以把代码优化到 35pts(这个代码我没写,大家自己去尝试)。
然后观察那个 DP 式子,我们会发现 f i , j f_{i,j} fi,j 其实就是由 f i , j − ( i − b ) , f i , j − 2 ( i − b ) , … , f i , j − k ( i − b ) f_{i,j-(i-b)},f_{i,j-2(i-b)},\dots,f_{i,j-k(i-b)} fi,j−(i−b),fi,j−2(i−b),…,fi,j−k(i−b) 全加一起得到的,因此我们可以考虑一个神秘的前缀和(跨度是 k k k),然后里面的转移就可以从 O ( k ) O(k) O(k) 变成 O(1)$,实测可以拿到 70pts。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353,p=1500000;
int k,q,n,b,mn,mx,t,a[156],tag[3000006],s[3000006],f[2][3000006];
signed main()
{
cin>>k>>q;
while(q--)
{
t++;
cin>>n>>b;
for(int i=1;i<=n;i++)
{
a[i]=b-i;
}
f[0][p]=1;
tag[p]=t;
mn=p,mx=p;
for(int i=1;i<=n;i++)
{
int now=i&1,odd=(i&1)^1;
if(a[i]>0)
{
mx+=a[i]*k;
}
else
{
mn+=a[i]*k;
}
mx=max(mx,0ll);
mn=min(mn,3000000ll);
for(int j=mn;j<=mx;j++)
{
f[now][j]=0;
}
if(a[i]==0)
{
for(int j=mn;j<=mx;j++)
{
if(tag[j]!=t)
{
continue;
}
f[now][j]=f[odd][j]*(k+1)%mod;
tag[j]=t;
}
continue;
}
else if(a[i]>0)
{
for(int j=mn;j<=mx;j++)
{
s[j]=(tag[j]==t?f[odd][j]:0);
if(j-a[i]<mn||j-a[i]>mx)
{
continue;
}
s[j]+=s[j-a[i]];
if(s[j]>=mod)
{
s[j]-=mod;
}
}
}
else
{
for(int j=mx;j>=mn;j--)
{
s[j]=(tag[j]==t?f[odd][j]:0);
if(j-a[i]<mn||j-a[i]>mx)
{
continue;
}
s[j]+=s[j-a[i]];
if(s[j]>=mod)
{
s[j]-=mod;
}
}
}
int d=(k+1)*a[i];
for(int j=mn;j<=mx;j++)
{
int e=j-d,v=s[j];
if(e>=mn&&e<=mx)
{
v-=s[e];
if(v<0)
{
v+=mod;
}
if(v>=mod)
{
v-=mod;
}
}
f[now][j]=v;
tag[j]=t;
}
}
cout<<(f[n&1][p]-1+mod)%mod<<'\n';
}
return 0;
}
对于满分做法, 我们考虑预处理和 meet-in-the-middle(分治)。
我们观察 i − b i-b i−b 这个式子,其实它就是由这些东西构成的:
1 − b , 2 − b , 3 − b , … , − 1 , 0 , 1 , … , n − b 1-b,2-b,3-b,\dots,-1,0,1,\dots,n-b 1−b,2−b,3−b,…,−1,0,1,…,n−b
我们要让整个式子的和为 0 0 0,其实就是要让负数部分的和和正数部分的和互为相反数,其实就是绝对值相等,因此我们不改 DP 定义,但是把整个数列分成两部分,分而治之,最后用组合数学算出答案。
因为 0 0 0 选不选都可以,所以 0 0 0 每次对答案的贡献就是 k + 1 k+1 k+1。
代码:
#include<bits/stdc++.h>
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353;
int k,q,n,b,mx[156];
long long f[156][300006];//手算一下就会发现左右和最小的最大就是接近三十万
signed main()
{
cin>>k>>q;
for(int i=1;i<=150;i++)
{
mx[i]=mx[i-1]+i*k;
}
f[0][0]=1;
for(int i=1;i<=150;i++)
{
for(int j=0;j<=min(mx[i],300000ll);j++)
{
f[i][j]=f[i-1][j];
if(j>=i)
{
f[i][j]=(f[i][j]+f[i][j-i])%mod;
if(j>=(k+1)*i)
{
f[i][j]=(f[i][j]-f[i-1][j-(k+1)*i]+mod)%mod;
}
}
}
}
while(q--)
{
cin>>n>>b;
int ans=0;
for(int i=0;i<=min(mx[b-1],mx[n-b]);i++)
{
ans=(ans+f[b-1][i]*f[n-b][i]%mod*(k+1)%mod)%mod;
}
cout<<(ans-1+mod)%mod<<'\n';
}
return 0;
}
T4
题面:


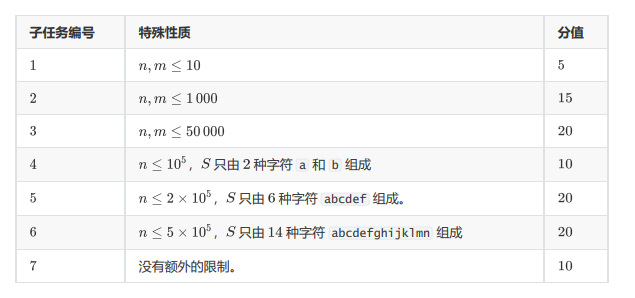
特殊性质啥的我就不讲了,这里直接讲正解。
(个人感觉 T4 比 T3 好写)。
首先看到这题,很容易想到枚举每个位置,然后找前一个和它能够拼在一起的位置,把长度加一来转移。但是有个问题:上一个位置究竟是哪种字母呢?因为题目只要求和当前这一位不一样就行,所以我们没法确定是哪种字母。因此我们直接更改 DP:设 f i , j f_{i,j} fi,j 表示考虑到第 i i i 位,上一个字母是 j j j(这里用数字替代字母)。当然不能和当前这一位的字母相同。
然后就是找到上一个出现这个字母的位置,这个位置明显可以通过预处理出来,因此目前时间复杂度还是 O ( 26 n ) O(26n) O(26n) 的,可以接受。
然后就是查询部分。我们可以考虑枚举是哪两个字母(反正查询次数很小,可以接受 2 6 2 26^2 262),当然,还是保证这两个字母不同。我们认定第一个枚举的字母是第一个出现的,于是我们可以找到这两个字母在这个区间内第一次出现的位置和最后一次出现的位置,因为我们不知道最后一个字母会是什么,所以我们两种都算一遍。
然后就可以算出答案了。
代码:
#include<bits/stdc++.h>
#define code using
#define by namespace
#define plh std
code by plh;
int n,la[1500006][26],nx[1500006][26],f[1500006][26];
string s;
signed main()
{
cin>>s;
n=s.size();
s=" "+s;
for(int i=1;i<=n;i++)
{
for(int j=0;j<26;j++)
{
la[i][j]=la[i-1][j];
}
la[i][s[i]-'a']=i;
}
for(int i=0;i<26;i++)
{
la[n+1][i]=la[n][i];
}
for(int i=0;i<26;i++)
{
nx[n+1][i]=n+1;
}
for(int i=n;i>=1;i--)
{
for(int j=0;j<26;j++)
{
nx[i][j]=nx[i+1][j];
}
nx[i][s[i]-'a']=i;
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<26;j++)
{
if(j==s[i]-'a')
{
continue;
}
f[i][j]=f[la[i][j]][s[i]-'a']+1;
}
}
int q;
cin>>q;
while(q--)
{
int l,r,ans=0;
char c1,c2;
cin>>l>>r;
for(int i=0;i<26;i++)
{
for(int j=0;j<26;j++)
{
if(i==j)
{
continue;
}
int L=nx[l][i],R1=la[r][i],R2=la[r][j];
if(L>r)
{
continue;
}
if(R1>R2)
{
int num=f[R1][j]-f[L][j]+1;
if(num>ans)
{
ans=num;
c1=i+'a';
c2=j+'a';
}
}
else
{
int num=f[R2][i]-f[L][j]+1;
if(num>ans)
{
ans=num;
c1=i+'a';
c2=j+'a';
}
}
}
}
cout<<ans<<" "<<c1<<c2<<'\n';
}
return 0;
}





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








