MX模拟赛四总结

最新推荐文章于 2025-12-02 19:20:40 发布

原创最新推荐文章于 2025-12-02 19:20:40 发布 · 737 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #图论

比赛总结专栏收录该内容

27 篇文章

订阅专栏

又是被 freopen 背刺的一天……

T1

题面：

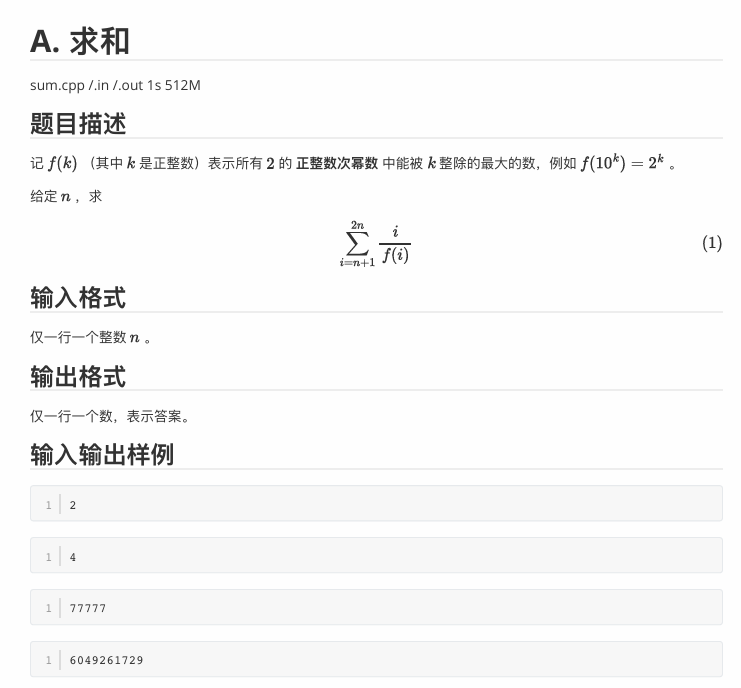
上来一道诈骗题……

其实我们把题意稍微转化一下就是把 $n + 1$ 到 $2 n$ 之间所有的数一直除以 $2$ ，直到这个数变成奇数为止。

我们可以先列举一些例子：

2~2:1
3~4:1,3
4~6:1,3,5

我们会发现，这个区间内的奇数只可能会出现一次！我们尝试来证明一下这个结论。

假设 $n+1≤f(i)i≤2nn+1\le\frac{f(i)}{i}\le2n$ ，那只有当 $f(i)i\frac{f(i)}{i}$ 乘了 $2$ 才有可能出现重复的情况，我们来算一算：

$2n<2n+2≤2f(i)i2n\lt2n+2\le\cfrac{2f(i)}{i}$

因此这个“可能出现的数”一定不可能出现。

所以我们也就证明了在 $n+1→2nn+1\to2n$ 之间的奇数只会出现一次。

那么最终的总和就是 $1+3+5+…1+3+5+\dots$ ，这个的结果是多少呢？其实就是 $n^2$ 。所以直接输入 $n$ ，然后输出 $n^2$ 就行了。总之纯诈骗题。

T2

题面：

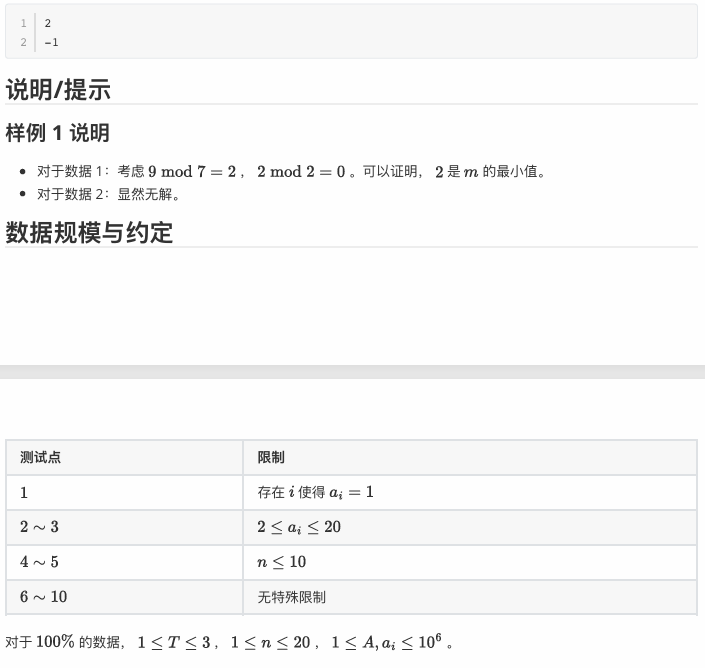
这个题有很多做法，比如说有暴力 dfs、DP、枚举加贪心，这里我主要讲一下枚举这种做法。

因为 $n≤20n\le20$ ，所以我们可以直接二进制枚举，其中 $1$ 表示要用， $0$ 表示不用，且要用就必须全用完，这里的用不是说把它拿去取一下模就行，而是必须要让 A 减少。

那我们思考一个问题：这些数选出来了，该按照什么样的顺序去取模呢？假设我们取出来 $m$ 个数，且满足 $a1≤a2≤⋯≤ama_1\le a_2\le\dots\le a_m$ ，因为我们定义了取出来就必须“用”，所以如果我们上来就对 $ai(i<m)a_i(i\lt m)$ 取模，那 $i+1→mi+1\to m$ 的这些数就都没有用了，因为 $ai<ai≤amA\bmod a_i\lt a_i\le a_m$ 。所以最优策略一定是从大到小取模。

所以代码就很简单了：首先对 $a$ 数组从大到小排序，然后暴力枚举，总时间复杂度 $O(T(n\log n+2^nn))$ 。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int t,n,A,ans=LONG_LONG_MAX,a[26];
bool cmp(int x,int y)
{
    return x>y;
}
bool check(int x)
{
    int k=A;
    for(int i=1;i<=n;i++)
    {
        if((1<<i-1)&x)
        {
            k%=a[i];
        }
    }
    return k==0;
}
signed main()
{
    cin>>t;
    while(t--)
    {
        ans=LONG_LONG_MAX;
        cin>>n>>A;
        bool fl=false;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
            if(a[i]==1)
            {
                fl=true;
            }
        }
        sort(a+1,a+n+1,cmp);
        if(fl)
        {
            cout<<1<<'\n';
            continue;
        }
        int m=(1<<n)-1;
        for(int i=0;i<=m;i++)
        {
            if(check(i))
            {
                ans=min(ans,(int)(__builtin_popcount(i)));
            }
        }
        cout<<(ans>1e9?-1:ans)<<'\n';
    }
    return 0;
}

T3

题面：

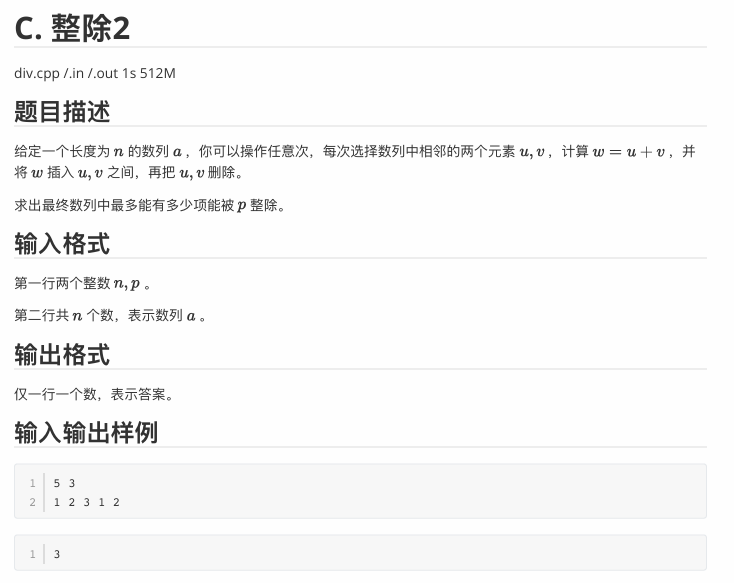
又是一道水题……

题解中给的做法是 DP，但是实际上并不用，这题贪心就可以解决。

因为要求区间和，所以我们上来肯定首先要求前缀和（求区间和的好方法），又因为要被 $p$ 整除，所以我们可以考虑把前缀和数组全模一个 $p$ ，这样当余数相同的时候两数相减就必定是 $0$ ，也就是说中间的数的和一定是 $p$ 的倍数。

然后这道题就做出来了。

对于所有区间，我们肯定是能取的必定取，所以从前往后贪心的扫一遍，记录在当前节点之前有没有余数相同的节点，如果有，直接计入答案，并把前面所有的数全标记成 -1（防止再次被用），然后就 AC 了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,p,ans,a[1000006],s[1000006],b[1000006];
signed main()
{
    cin>>n>>p;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        s[i]=(s[i-1]+a[i])%p;
    }
    b[0]=1;
    for(int i=1;i<=n;i++)
    {
        if(b[s[i]])
        {
            ans++;
            for(int j=i-1;j>=0;j--)
            {
                if(s[j]==-1)
                {
                    break;
                }
                b[s[j]]=0;
                s[j]=-1;
            }
        }
        b[s[i]]=1;
    }
    cout<<ans;
    return 0;
}

T4

题面：

这个题首先一眼 DP。

因为我们要算的是从一个节点划开，前后满足题目条件子串有多少。其实我们也可以反过来看，即从 $i$ 和 $j$ 出发的两个子串对哪些节点的值有多少贡献。

因此我们可以设 $f_{i,j}$ 表示以 $i,j(i<j)i,j(i\lt j)$ 两点作为起点往后延伸，能在满足题目条件的情况下能延伸的最大长度是多少。

为了便于转移，我们枚举 $i, j$ 之间的距离 $d$ ，于是 $j = i + d$ ，并且保证在转移过程中距离不变。

因此我们只有一种转移方向： $fi,j→fi+1,j+1f_{i,j}\to f_{i+1,j+1}$ 。

假设我们已知 $f_{i,j}=L$ ，要算 $f_{i+1,j+1}$ ，我们先画个图来看一看：

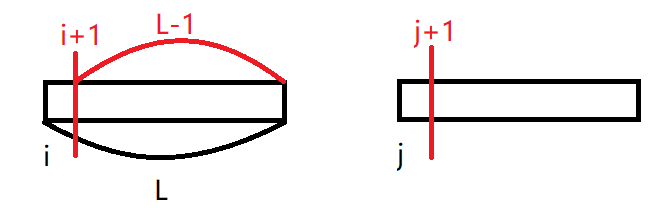
我们已知那一段长度为 $L$ 的子串是符合题目要求的，因此另一段长度为 $L - 1$ 的子串也肯定是合法的，现在的问题就是中间空出来的那一段该怎么办。

因为我们并不知道以 $i$ 开头的那一段子串里与后面 $j$ 开头的那一段子串里不同的字符有多少，所以这里我们还需要设一个 $g_{i,j}$ ，定义就是记录不同的字符有多少。

所以，长度为 $L - 1$ 的那段子串的 $g$ 我们就可以轻松求出来： $gi+1,j+1=gi,j−[si≠sj]g_{i+1,j+1}=g_{i,j}-[s_i\not=s_j]$ 。然后我们就可以往后延伸了。注意在延伸过程中也要记录不同的字符对数。

然后我们也可以在 $L - 1$ 的基础上计算 $f_{i+1,j+1}$ 的值了。

最后就是统计答案，我们设 $ans_i$ 表示从 $i$ 后面划开的答案数，于是我们就可以计算出贡献：

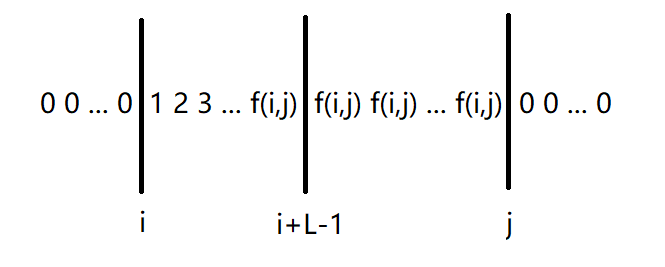
具体原因请读者自证。

我们做一次差分，就得到了：

0 0 ... 0 1 1 ... 1 0 0 ... 0 -f[i][j] 0 0 ... 0

再做一次差分，就得到了：

0 0 ... 0 1 0 ... 0 -1 0 ... 0 -f[i][j] f[i][j] 0 0 ... 0

我们会发现，实际上就是在 $i$ 处加了 $1$ ，在 $i + L$ 处减了 $1$ ，在 $j$ 处减了 $f_{i,j}$ ，在 $j + 1$ 处加了 $f_{i,j}$ ，因此对于任意的一对 $(i, j)$ ，都有这个公式可以计算。最后做两遍前缀和就行了。

代码：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,k,f[3006][3006],g[3006][3006],ans[3006];
string s;
signed main()
{
    cin>>n>>k;
    cin>>s;
    s=" "+s;
    for(int d=1;d<n;d++)
    {
        int j=1+d,sum=0,l;
        for(l=0;j+l<=n&&1+l<j;l++)
        {
            sum+=(s[1+l]!=s[j+l]);
            if(sum>k)
            {
                sum--;
                break;
            }
        }
        f[1][j]=l;
        g[1][j]=sum;
    }
    for(int d=1;d<n;d++)
    {
        for(int i=1;i+d<n;i++)
        {
            int j=i+d;
            int L=f[i][j]-1;
            if(L<=0)
            {
                int sum=0;
                for(L=0;j+1+L<=n&&i+1+L<j+1;L++)
                {
                    sum+=(s[i+1+L]!=s[j+1+L]);
                    if(sum>k)
                    {
                        sum--;
                        break;
                    }
                }
                f[i+1][j+1]=L;
                g[i+1][j+1]=sum;
                continue;
            }
            int sum=g[i][j]-(s[i]!=s[j]);
            if(sum<k)
            {
                for(;j+1+L<=n&&i+1+L<j+1;L++)
                {
                    sum+=(s[i+1+L]!=s[j+1+L]);
                    if(sum>k)
                    {
                        sum--;
                        break;
                    }
                }
            }
            f[i+1][j+1]=L;
            g[i+1][j+1]=sum;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            ans[i]+=1,ans[i+f[i][j]]-=1,ans[j]-=f[i][j],ans[j+1]+=f[i][j];
        }
    }
    for(int i=1;i<=n;i++)
    {
        ans[i]+=ans[i-1];
    }
    for(int i=1;i<=n;i++)
    {
        ans[i]+=ans[i-1];
    }
    for(int i=1;i<n;i++)
    {
        cout<<ans[i]<<'\n';
    }
    return 0;
}

T5

题面：

看着是一道数学题，但它其实还是一道 DP！

我们设 $f_{i,j}$ 表示前 $i$ 项中总和模 $k$ 等于 $j$ 的子序列数。那么我们可以轻易地转移这个 DP：

$k+fi,jf_{i+1,j}=f_{i+1,j}+f_{i,j},f_{i+1,(j+a_{i+1})\bmod k}=f_{i+1,(j+a_i)\bmod k}+f_{i,j}$

即这个子序列可以选择加入 $a_{i+1}$ ，也可以选择不加入。

现在就是这个算答案的问题了。

如果前面有一个序列让 $a_{i+1}$ 加入，那它能额外带来的贡献是 $⌊j+ai+1k⌋\lfloor\frac{j+a_{i+1}}{k}\rfloor$ ，那对多少个序列产生了这种额外的贡献呢？首先在后面的肯定有 $f_{i,j}$ 个，其次在它前面有 $n - i - 1$ 个数，这些数对这次贡献不会有什么影响，所以又会有 $2^{n-i-1}$ 个，总的来讲，就有 $dpi,j×2n−i−1dp_{i,j}\times2^{n-i-1}$ 个。

然后代码就很好写了：

#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int n,k,p,ans,a[5006],pw[5006],dp[5006][5006];
signed main()
{
    cin>>n>>k>>p;
    const int m=static_cast<const int>(p);
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    pw[0]=1;
    for(int i=1;i<=n;i++)
    {
        pw[i]=pw[i-1]*2%m;
    }
    dp[0][0]=1;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<k;j++)
        {
            if(j+a[i+1]>=k)
            {
                ans=(ans+(j+a[i+1])/k*dp[i][j]%m*pw[n-i-1]%m)%m;
            }
            dp[i+1][j]=(dp[i+1][j]+dp[i][j])%m;
            dp[i+1][(j+a[i+1]%k)%k]=(dp[i+1][(j+a[i+1]%k)%k]+dp[i][j])%m;
        }
    }
    cout<<ans;
    return 0;
}

总结

T1:0/100，freopen 写错了，最不应该出现的错误还是一不小心出现了。
T2:50/100，排序那个地方没太处理好，当时是在函数里排的序，所以时间复杂度稍微有点问题，另外就是在函数里额外多开了一个 vector，常数有点大，被卡 T 了。
T3：20/30，没仔细看，多了一个点 WA 了。
T4：50/60，同样的，多了一个点 WA。
T5；20/20。

总之，本人对这次考试成绩十分不满意，因为中间时间安排也有点问题，导致最终最多只有 290pts，望下次改正。