前言
又是被坑惨的一天……
T1
题面:



一道很水的组合计数题,只需要记录下有多少人数是比当前人数要小的,然后用点组合数学的知识就能解决。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353;
struct brain{
int x,id;
}a[1000006];
int n,m,k,ans[1000006],fac[1000006],inv[1000006];
int C(int x,int y)
{
return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int qpow(int x,int y)
{
int z=1;
while(y)
{
if(y&1)
{
z=z*x%mod;
}
x=x*x%mod;
y>>=1;
}
return z;
}
int read()
{
int z=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')
{
f=-1;
}
c=getchar();
}
while(c>='0'&&c<='9')
{
z=(z<<3)+(z<<1)+(c^48);
c=getchar();
}
return z*f;
}
signed main()
{
// freopen("brain.in","r",stdin);
// freopen("brain.out","w",stdout);
n=read(),m=read(),k=read();
for(int i=1;i<=m;i++)
{
a[i].x=read();
a[i].id=i;
}
fac[0]=1;
for(int i=1;i<=m;i++)
{
fac[i]=fac[i-1]*i%mod;
}
inv[m]=qpow(fac[m],mod-2);
for(int i=m-1;i>=0;i--)
{
inv[i]=inv[i+1]*(i+1)%mod;
}
sort(a+1,a+m+1,[&](brain x,brain y)
{
return x.x<y.x;
});
for(int i=k;i<=m;i++)
{
ans[a[i].id]=C(i-1,k-1);
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<" ";
}
return 0;
}
T2
题面:
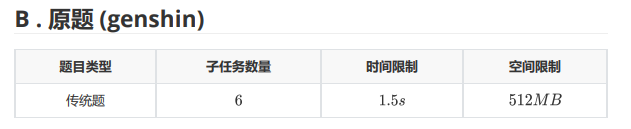

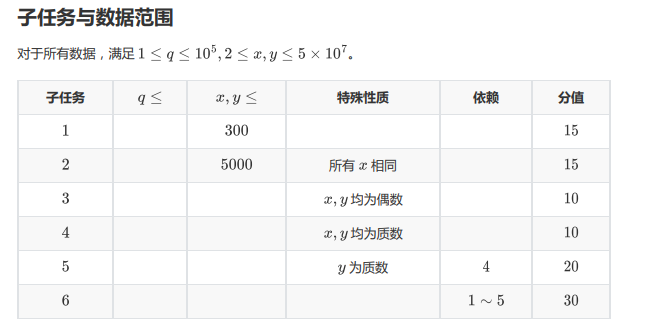
(很可惜,我没做过这道原题)。
首先,一共有 10100−110^{100}-110100−1 个点,想要直接连边明显不行,那这题肯定就是一道数学题了。
我们首先来思考一种非常简单的情况:如果 xxx 与 yyy 互质呢?
在这种情况下,lcm(x,y)=xy\operatorname{lcm}(x,y)=xylcm(x,y)=xy,所以从 xxx 直接走到 yyy 似乎不是很优。
我们来思考一下有没有办法让这个过程中产生的代价更小,有一种办法就是让 xxx 走到 xxx 的倍数,yyy 走到 yyy 的倍数,然后把这两个倍数相连,但我们稍微用一点点简单的运算就很容易知道这种情况下比直接走过去还要更长,证明如下:
证明:设 x→kxx\to kxx→kx,y→tyy\to tyy→ty(k,t∈Zk,t\isin\Zk,t∈Z),则:
∴sum=kx+lcm(kx,ty)+ty\therefore sum=kx+\operatorname{lcm}(kx,ty)+ty∴sum=kx+lcm(kx,ty)+ty
∵lcm(kx,ty)=ktxygcd(kx,ty)=ktxygcd(k,t)\because\operatorname{lcm}(kx,ty)=\cfrac{ktxy}{\gcd(kx,ty)}=\cfrac{ktxy}{\gcd(k,t)}∵lcm(kx,ty)=gcd(kx,ty)ktxy=gcd(k,t)ktxy
∴lcm(kx,ty)=ktgcd(k,t)xy≥xy\therefore\operatorname{lcm}(kx,ty)=\cfrac{kt}{\gcd(k,t)}xy\ge xy∴lcm(kx,ty)=gcd(k,t)ktxy≥xy
∴sum>xy\therefore sum\gt xy∴sum>xy
得证。
如果你说不往 xxx 的倍数走,往一个比较小的数 ttt 走,那最坏情况下代价也就 (x+y)t(x+y)t(x+y)t,那我就很好奇了:为什么你不往 222 走呢?这样最坏情况下也就是 2(x+y)2(x+y)2(x+y),比上面那种情况要优多了。
所以我们就得到了另一种很朴素的方法:把 222 作为中转点走,代价为 lcm(2,x)+lcm(2,y)\operatorname{lcm}(2,x)+\operatorname{lcm}(2,y)lcm(2,x)+lcm(2,y)。
既然我们想到了可以往小的走,那为什么我们不能往一个数的最小质因数走呢?于是我们得到了三种很神奇的方法:
- 以 xxx 的最小质因数为中转点,代价为 x+dx⋅yx+dx\cdot yx+dx⋅y。
- 以 yyy 的最小质因数为中转点,代价为 x⋅dy+yx\cdot dy+yx⋅dy+y。
- 以 xxx 的最小质因数和 yyy 的最小质因数为中转点,代价为 x+dx⋅dy+yx+dx\cdot dy+yx+dx⋅dy+y。
其中,dxdxdx 表示 xxx 的最小质因数,dydydy 表示 yyy 的最小质因数。
当然,我们在 dxdxdx 和 dydydy 之间也可以安排 222 作为中转点,这中间的情况就稍微有点复杂了,这里不展开讲。
现在我们考虑另一种情况:xxx 与 yyy 不互质的时候。
首先上面的基本操作肯定有(注意这里的 dxdxdx 与 dydydy 可能相等,所以从 dxdxdx 走到 dydydy 的代价就有可能是 000),其次就是这种情况特有的东西:即它可以从它们的最大公因数走过去,即路径是这样的:x→gcd(x,y)→yx\to\gcd(x,y)\to yx→gcd(x,y)→y。这时的代价为 x+yx+yx+y。
然后这道题就做完了。
说白了就是一道数学题,可惜考试的时候没判断 x=yx=yx=y 的情况,炸惨了。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
int q;
bool b[50000006];
vector<int>v;
int len(int x,int y)
{
if(x==y)
{
return 0;
}
return x*y/(__gcd(x,y));
}
int ans(int x,int y,int xx,int yy)
{
int s=LONG_LONG_MAX;
if(__gcd(x,y)!=1)
{
s=min(s,len(x,__gcd(x,y))+len(y,__gcd(x,y)));
}
return min({s,len(x,y),len(x,2)+len(2,y),len(x,xx)+len(xx,y),len(x,yy)+len(yy,y),len(x,xx)+len(xx,2)+len(2,y),len(x,2)+len(2,yy)+len(yy,y),len(x,xx)+len(xx,yy)+len(yy,y),len(x,xx)+len(xx,2)+len(2,yy)+len(yy,y)});
//这里比较暴力,我直接枚举完所有情况算的。
}
signed main()
{
for(int i=2;i<=50000000;i++)//线性筛,注意:这里用埃氏筛或在询问时用根号级别的筛法都会 TLE
{
if(!b[i])
{
v.push_back(i);
}
for(auto j:v)
{
if(j*i>50000000)
{
break;
}
b[j*i]=1;
}
}
cin>>q;
while(q--)
{
int x,y;
cin>>x>>y;
int xx=LONG_LONG_MAX,yy=LONG_LONG_MAX;
if(!b[x])
{
xx=x;
}
else
{
for(auto i:v)
{
if(x%i==0)
{
xx=i;
break;
}
}
}
if(!b[y])
{
yy=y;
}
else
{
for(auto i:v)
{
if(y%i==0)
{
yy=i;
break;
}
}
}
cout<<ans(x,y,xx,yy)<<'\n';
}
return 0;
}
T3
题面:
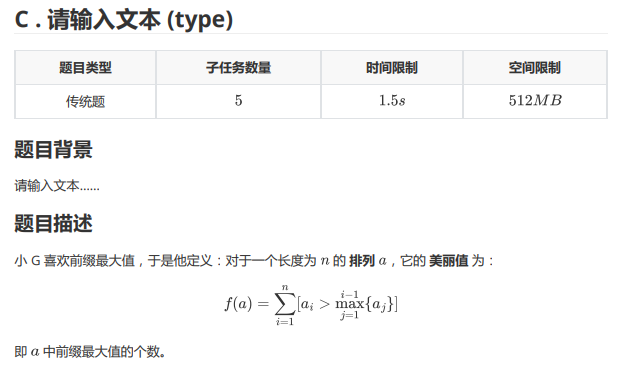


其实这是一道 T4 级别的题……
首先对于算个数这种题,我们很容易想到算每个区间的贡献是多少。并且能够很容易的写出下面这个式子:
ans=∑i=lr(i−max(bi,l−1))×(r−i+1) ans=\sum_{i=l}^r(i-\max(b_i,l-1))\times(r-i+1) ans=i=l∑r(i−max(bi,l−1))×(r−i+1)
其中 bib_ibi 指 iii 前面第一个大于 aia_iai 的数的位置。
意思就是指当 LLL 取 max(bi+1,l)→i\max(b_i+1,l)\to imax(bi+1,l)→i 之间的任何数时,RRR 取 i→ri\to ri→r 之间任何一个数都会有贡献。
但是我们看到这个 max\maxmax 有点烦,于是我们可以把它拆开:
ans=∑i=lr(i−bi)×(r−i+1)−∑i=lr[bi<l](l−bi−1)×(r−i+1) ans=\sum_{i=l}^r(i-b_i)\times(r-i+1)-\sum_{i=l}^r[b_i\lt l](l-b_i-1)\times(r-i+1) ans=i=l∑r(i−bi)×(r−i+1)−i=l∑r[bi<l](l−bi−1)×(r−i+1)
再拆一下:
ans=r∑i=1r(i−bi)−∑i=lr(i−bi)(i−1)−(∑i=lr[bi<l](l−1)(r+1)−∑i=lr[bi<l]bi(r+1)−∑i=lr[bi<l]i(l−1)+∑i=lr[bi<l]ibi) ans=r\sum_{i=1}^r(i-b_i)-\sum_{i=l}^r(i-b_i)(i-1)-(\sum_{i=l}^r[b_i\lt l](l-1)(r+1)-\sum_{i=l}^r[b_i\lt l]b_i(r+1)-\sum_{i=l}^r[b_i\lt l]i(l-1)+\sum_{i=l}^r[b_i\lt l]ib_i) ans=ri=1∑r(i−bi)−i=l∑r(i−bi)(i−1)−(i=l∑r[bi<l](l−1)(r+1)−i=l∑r[bi<l]bi(r+1)−i=l∑r[bi<l]i(l−1)+i=l∑r[bi<l]ibi)
对于前面两项,很明显可以用两个前缀和维护,对于后面几项,则稍微复杂一点。
我们把这四项分个类:
(l−1)(r+1)∑1(r−1)∑bi(l+1)∑i∑ibi (l-1)(r+1)\sum1 \\ (r-1)\sum b_i \\ (l+1)\sum i \\ \sum ib_i (l−1)(r+1)∑1(r−1)∑bi(l+1)∑i∑ibi
对于每一类,我们可以看做二维数点:即把 bib_ibi 看做横坐标、把 iii 看做纵坐标,然后就是求横坐标在 [1,l)[1,l)[1,l)、纵坐标在 [l,r][l,r][l,r] 里面的点的上述的总和是多少。
因为有两个参数不好维护,所以我们可以采用离线处理,然后按照 lll 从小到大排序,这样每次就只会多考虑点(因为横坐标要小于 lll),那对于每个多考虑的点,我们以纵坐标为编号,用树状数组(或线段树,不过有点小题大做了)维护,按照四类用四个树状数组,分别维护 111、iii、bib_ibi、ibiib_iibi 四种的前缀和,然后用前缀和的方法求出编号在 [l,r][l,r][l,r] 之间的所有点这四种的和到底是多少,然后带入公式,就做完了。
时间复杂度:O(qlogn)O(q\log n)O(qlogn)。
其实这题也可以强制在线,用主席树(可持久化线段树)就可以做到,不过这样的话空间可能不太够,用动态开点或许可以。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
struct ask{
int l,r,id;
}q[1000006];
struct Node{
int x,y;
}node[1000006];
int n,m,a[1000006],b[1000006],s[2][1000006],tr[6][1000006],ans[1000006];
#define lowbit(x) (x&-x)
void update(int id,int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
{
tr[id][i]+=y;
}
}
int query(int id,int x)
{
int sum=0;
for(int i=x;i;i-=lowbit(i))
{
sum+=tr[id][i];
}
return sum;
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=m;i++)
{
cin>>q[i].l>>q[i].r;
q[i].id=i;
}
stack<pair<int,int>>st;
st.push(make_pair(LONG_LONG_MAX,0));
for(int i=1;i<=n;i++)
{
while(!st.empty()&&st.top().first<a[i])
{
st.pop();
}
b[i]=st.top().second;
st.push(make_pair(a[i],i));
}
for(int i=1;i<=n;i++)
{
node[i].x=b[i],node[i].y=i;
s[0][i]=s[0][i-1]+(i-b[i]);
s[1][i]=s[1][i-1]+(i-1)*(i-b[i]);
}
sort(q+1,q+m+1,[&](ask x,ask y)
{
return x.l<y.l;
});
sort(node+1,node+n+1,[&](Node x,Node y)
{
return x.x<y.x;
});
for(int i=1,j=1;i<=m;i++)
{
int l=q[i].l,r=q[i].r;
while(j<=n&&node[j].x<l)
{
update(1,node[j].y,1);
update(2,node[j].y,node[j].x);
update(3,node[j].y,node[j].y);
update(4,node[j].y,node[j].x*node[j].y);
j++;
}
ans[q[i].id]=r*(s[0][r]-s[0][l-1])-(s[1][r]-s[1][l-1])-((query(1,r)-query(1,l-1))*(l-1)*(r+1)-(query(2,r)-query(2,l-1))*(r+1)-(query(3,r)-query(3,l-1))*(l-1)+(query(4,r)-query(4,l-1)));
}
for(int i=1;i<=m;i++)
{
cout<<ans[i]<<'\n';
}
return 0;
}
T4
题面:


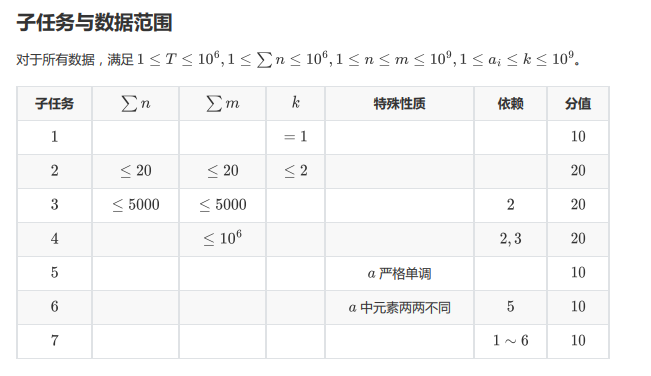
首先我们很容易想到:答案其实和 aaa 完全没有关系。
解释一下:我们如果在 aaa 之间插入一些数形成一个数列,那么我们只需要关注后面那个数是否与 aia_iai 一样,前面那个数则随便,这样正好能枚举完所有的情况,而这样则说明了我的答案与 aia_iai 是多少没有关系,只要后面那个数和它不相等就完了。
因此对于一种插入情况,我们一共有 (k−1)m−n(k-1)^{m-n}(k−1)m−n 种方案,而一共有 CmnC_m^nCmn 种情况,所以总的贡献应该是 Cmn(k−1)m−nC_m^n(k-1)^{m-n}Cmn(k−1)m−n。
当然,有的时候有些数是没法正好插入到两个数之间的,而有可能会被扔到两侧,这时我们可以把这些数看做是原本就固定的,而它后面的数不能和它一样。
因此,对于最终答案,很明显不是 Cmn(k−1)m−nC_m^n(k-1)^{m-n}Cmn(k−1)m−n。
为了方便后面表述,我们设 f(x)=Cmx(k−1)m−xf(x)=C_m^x(k-1)^{m-x}f(x)=Cmx(k−1)m−x,即有 xxx 个数固定时的总方案数。
按照我们上面说的:我们可以把一些数看做一开始就固定的数,这样就可以处理在两侧这种情况。因此最终答案应该是一个求和式:
∑i=nmf(i) \sum_{i=n}^mf(i) i=n∑mf(i)
因为我们发现 mmm 很大,所以我们可以考虑正难则反,即:
sum−∑i=0n−1f(i) sum-\sum_{i=0}^{n-1}f(i) sum−i=0∑n−1f(i)
其中这个 sumsumsum 怎么求呢?很容易想到:sum=∑i=0mf(i)sum=\sum_{i=0}^mf(i)sum=∑i=0mf(i),也就是说初始时没有固定的数的总方案数,那不就是每一位数都可以随便选吗。那就很简单了啊:明显 sum=kmsum=k^msum=km。
因此我们就得到了这样一个式子:
ans=km−∑i=0n−1f(i)=km−∑i=0n−1Cmi(k−1)m−i ans=k^m-\sum_{i=0}^{n-1}f(i)=k^m-\sum_{i=0}^{n-1}C_m^i(k-1)^{m-i} ans=km−i=0∑n−1f(i)=km−i=0∑n−1Cmi(k−1)m−i
最后一个问题:这个 CmiC_m^iCmi 怎么求?明显用一般的方法根本做不到,因此我们要考虑点不同寻常的方法。
我们尝试找 f(i−1)f(i-1)f(i−1) 与 f(i)f(i)f(i) 之间的关系,先写出两个式子:
f(i−1)=Cmi−1(k−1)m−i+1=m!(i−1)!(m−i+1)!(k−1)m−i+1f(i)=Cmi(k−1)m−i=m!i!(m−i)!(k−1)m−i f(i-1)=C_m^{i-1}(k-1)^{m-i+1}=\cfrac{m!}{(i-1)!(m-i+1)!}(k-1)^{m-i+1} \\ f(i)=C_m^i(k-1)^{m-i}=\cfrac{m!}{i!(m-i)!}(k-1)^{m-i} f(i−1)=Cmi−1(k−1)m−i+1=(i−1)!(m−i+1)!m!(k−1)m−i+1f(i)=Cmi(k−1)m−i=i!(m−i)!m!(k−1)m−i
这时我们不难发现这样一个等式:
f(i)=f(i−1)⋅1i⋅(m−i+1)⋅1k−1 f(i)=f(i-1)\cdot\cfrac{1}{i}\cdot(m-i+1)\cdot\cfrac{1}{k-1} f(i)=f(i−1)⋅i1⋅(m−i+1)⋅k−11
对于所有的除法,用逆元就行,然后顺着这个递推式子往下算就行了。
代码:
#include<bits/stdc++.h>
#define int long long
#define code using
#define by namespace
#define plh std
code by plh;
const int mod=998244353;
int t,n,m,k,a[1000006],f[1000006];
int qpow(int x,int y)
{
int z=1;
while(y)
{
if(y&1)
{
z=z*x%mod;
}
x=x*x%mod;
y>>=1;
}
return z;
}
signed main()
{
cin>>t;
while(t--)
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
f[0]=qpow(k-1,m);
for(int i=1;i<n;i++)
{
f[i]=f[i-1]*qpow(i,mod-2)%mod*(m-i+1)%mod*qpow(k-1,mod-2)%mod;
}
int ans=0;
for(int i=0;i<n;i++)
{
ans+=f[i];
ans%=mod;
}
cout<<(qpow(k,m)-ans+mod)%mod<<'\n';
}
return 0;
}





















 1214
1214

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








