算法题刷题记（数组类）——长度最小子数组

一、题目描述

1、需求说明

        给定一个含有n个正整数的数组和一个正整数target

        找出该数组中满足其总和大于等于target的长度最小的子数组[numsl, numsl+1, ..., numsr-1, numsr]，并返回其长度，如果不存在符合条件的子数组则返回0

        说明：

2、要求

        时间复杂度为O(n)

二、难点剖析与思路分解

1、题目理解

（1）需注意“子数组”一词，子数组是由数组切割而成的，而不完全是从数组中取几个元素组成的新数组。

（2）对时间复杂度要有概念，对时间复杂度有要求，意味着不能随意使用嵌套循环了。

2、算法设计

（1）O(n)意味着最多可以遍历一次数组，需要找到一个不需要回溯指针的方法，这种需求一般都需要至少两个指针完成。

（2）可以考虑某次求和结果是否可以继续使用，换句话说，下一次求和操作可能和上一次求和操作的操作数有很大部分是重复的，重复的操作数不需要再一次进行求和，由此可减少算力消耗。

（3）“两个指针”、“操作数重复”，根据这些关键思路可以设计出下图所示的算法。

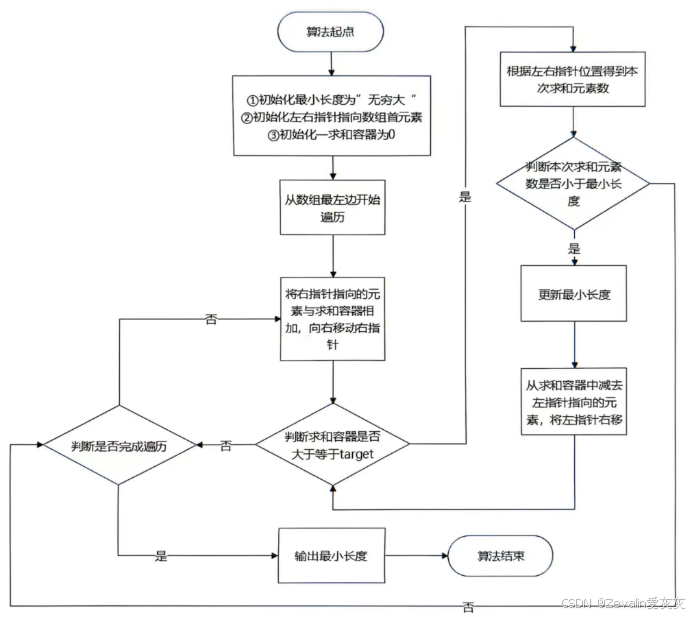
三、解题代码（C语言示例）

/*************************************************************
    函数作用：找出数组中满足其总和大于等于target的长度最小的子数组
    函数参数：
    tagrgt：子数组元素之和最小值
    nums：输入数组的首元素地址
    numsSize：输入数组的长度
**************************************************************/
int minSubArrayLen(int target, int* nums, int numsSize)
{
	
	int minLength = INT_MAX; 	     //初始化最小长度为“无穷大”
	int sum;                  		 //初始化一求和容器为0
	int left, right;              	 //初始化左右指针指向数组首元素
	
	do
	{
		sum += nums[right++]; 	    //将右指针指向的元素与求和容器相加，向右移动右指针
		
		while(sum >= target)  		//判断求和容器是否大于等于target，是则重复执行
		{
			int subLength = right - left;  //根据左右指针位置得到本次求和元素数
			minLength = minLength < subLength ? minLength : subLength;  //判断本次求和元素数是否小于最小长度，是则更新
			sum -= nums[left++];  //从求和容器中减去左指针指向的元素，将左指针右移
		}
	} while (right < numsSize);   //判断是否完成遍历

	//若minLength不为INT_MAX，则返回minLnegth
	return minLength == INT_MAX ? 0 : minLength;
}