一、直接计算DFT的问题及改进途径
1、直接计算DFT的问题

2、改善DFT运算效率的基本途径

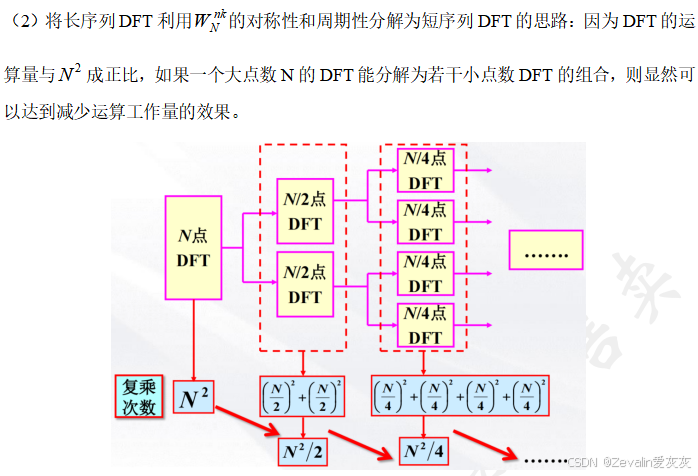
二、基于时间抽取的基-2-FFT快速算法
1、时间抽取的基-2-FFT快速算法条件

2、时间抽取的基-2-FFT快速算法原理分析

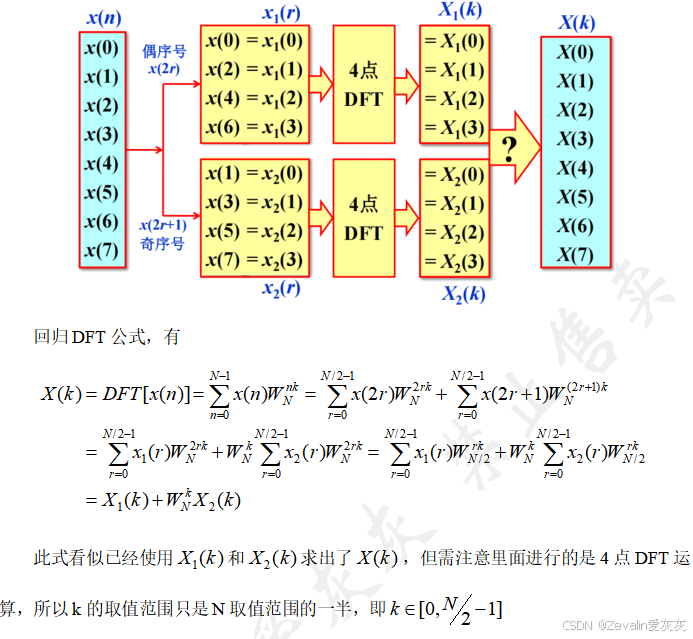
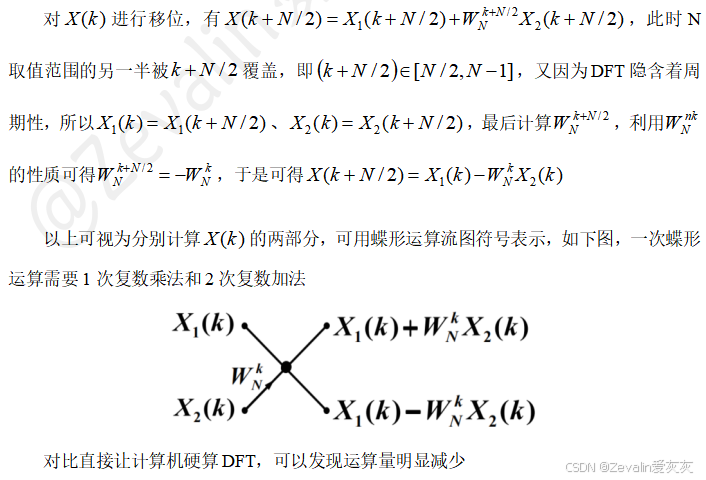
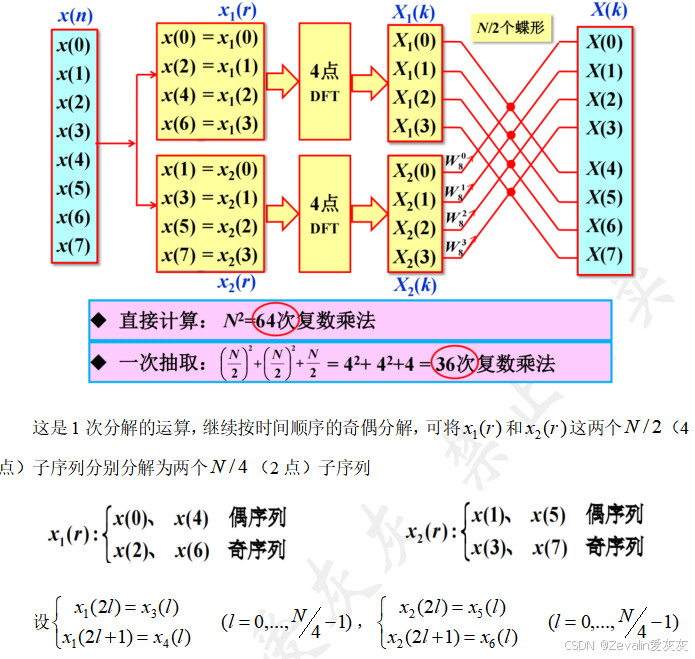


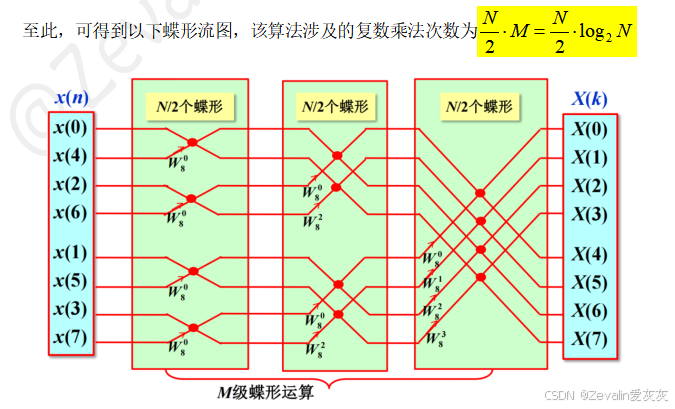
3、线性卷积和FFT方法求解LSI系统输出的运算量对比

4、时间抽取的基-2-FFT快速算法的编程方法
(1)原位运算(同址计算):
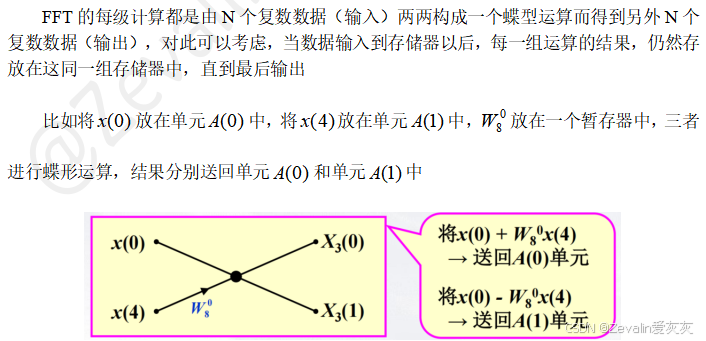
(2)旋转因子的变化规律:

(3)蝶形运算表示形式:

(4)FFT核心部分编程思想:
FFT核心部分编程即FFT的所有蝶形运算求解过程,流程图如下
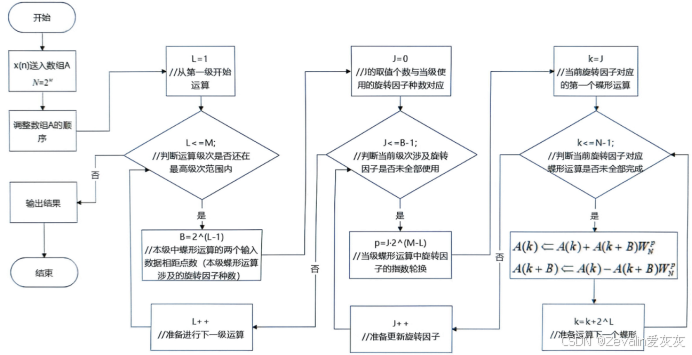
将此流程对应先前举的长度为8的FFT运算,中间变量的取值如下所示
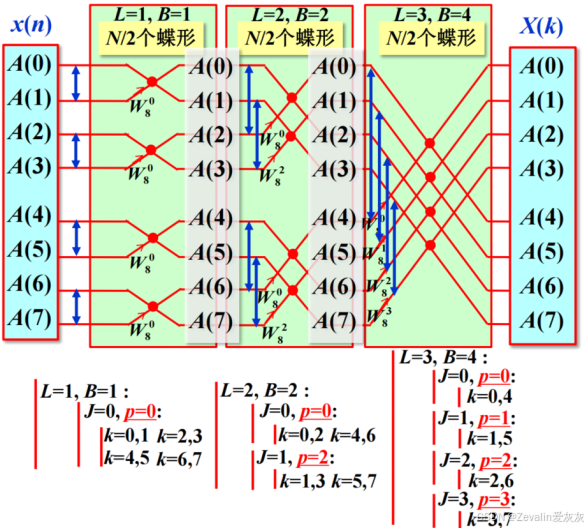
(5)码位倒序:

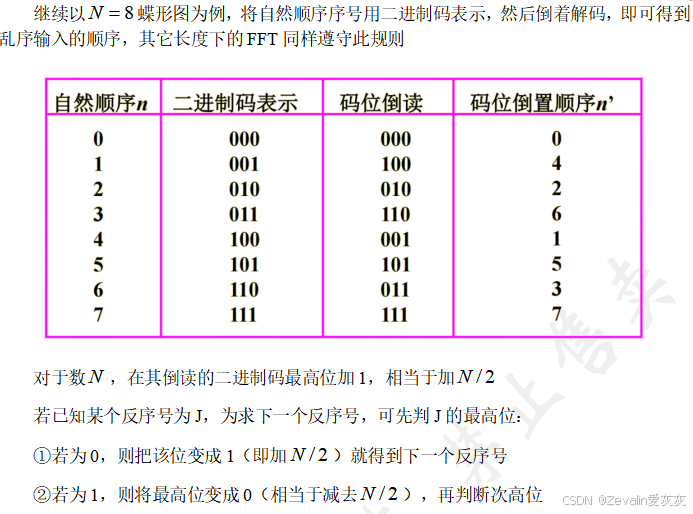
三、基于频率抽取的基-2-FFT快速算法
1、频率抽取的基-2-FFT快速算法介绍
(1)单个蝶形运算推导:


(2)假设对一个有限长序列进行8点DFT运算,借助频率抽取的基-2-FFT快速算法,其运算流图如下所示。
①DIF―FFT一次分解运算流图:
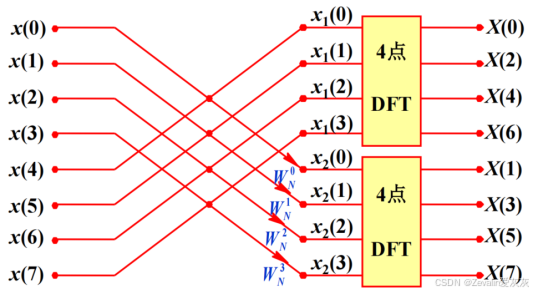
②DIF―FFT二次分解运算流图:
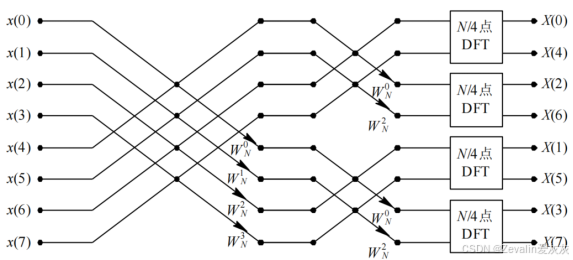
③DIF―FFT完全分解运算流图:
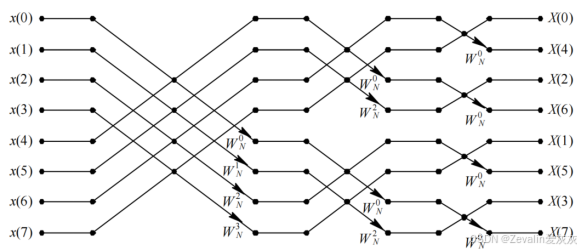
2、时间抽取算法与频率抽取算法的比较

四、快速傅里叶反变换的实现方法
1、借用FFT运算流图
(1)FFT算法流图也可以用于离散傅里叶逆变换(IDFT),比较DFT和IDFT的运算公式,可以发现它们十分相像,仅仅是旋转因子和系数发生了改变,运算流是不变的,所以可以考虑借用FFT的运算流图实现IDFT。
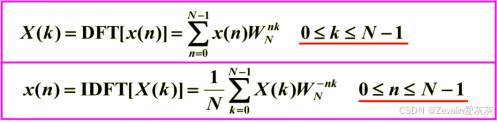
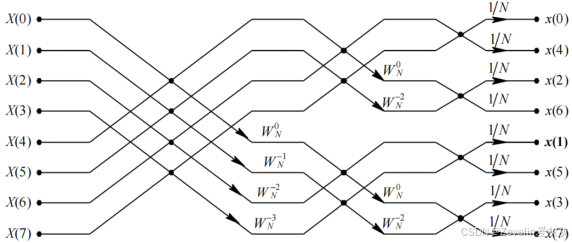
(2)继续以对一个有限长序列进行8点IDFT运算(N=8)为例,其运算流图如下所示,每个蝶形运算对应的旋转因子需要变更,最后输出时乘以1/N。
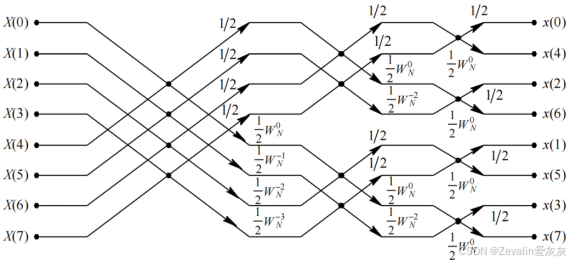
(3)当N比较大时,计算机直接处理1/N可能会引起精度问题,对此可以将1/N分解到每一级的运算中,尽可能地减少溢出之类的非预期现象。
2、借用FFT运算程序

五、进一步而减少运算量的措施
1、通过多类蝶形单元运算减少运算量
(1)一个旋转因子对应一个蝶形单元,如果处理好一些特殊旋转因子的乘法运算,对提升算力是有帮助的。
(2)多类蝶形单元:

(3)基2-FFT在各种蝶形单元下所需的实数乘法的次数:
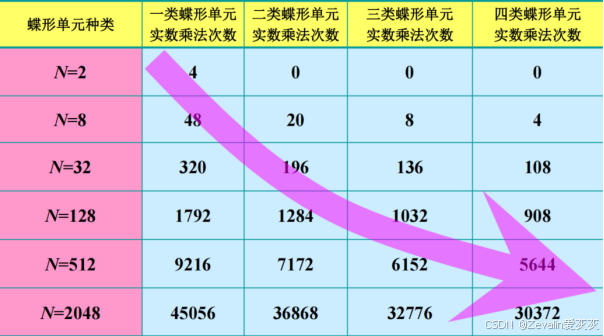
2、旋转因子查表代替运算
将旋转因子中正弦和余弦函数值存放在数组中,在程序执行时查表得到,比直接让程序计算正弦余弦值的效率更高
3、实序列的FFT算法
(1)用一次N点FFT计算两个N点的实序列的FFT:
一个实输入作为实部,另一个实输入作为虚部,计算完成后将结果进行简单的分解即可得到它们各自的FFT结果,这是利用了离散傅里叶变换的共轭对称性质
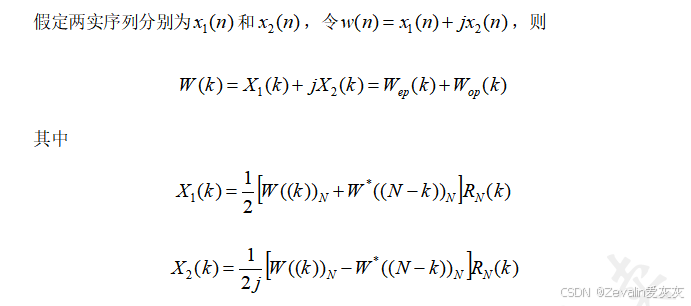
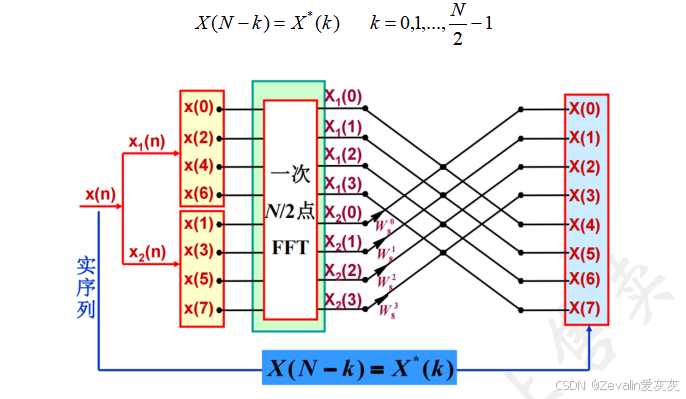
(2)用一次N/2点FFT计算一个N点的实序列的FFT:
在实际中更多的是仅对一个实序列进行FFT计算,对此可以将其拆成两个实序列,按上面的方法进行运算即可

六、线性调频z变换(CZT)
1、FFT的局限性
(1)z平面单位圆上的N个抽样点必须均匀等间隔地分布在范围中,且输入、输出的长度都是相同的N点,若需要提高窄带内的分辨率,运算流大且不划算。
(2)DFT只计算z平面单位圆上的抽样值,而有时需要求出非单位圆上的z变换抽样值,FFT是满足不了需求的。
(3)为解决FFT的局限性,引入了CZT算法,它是在更大z平面上的抽样z变换(没有单位圆的限制,没有等间隔点的限制)。
2、CZT算法介绍
(1)CZT算法的抽样过程:

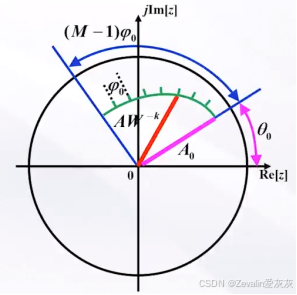
(2)CZT算法的计算公式:
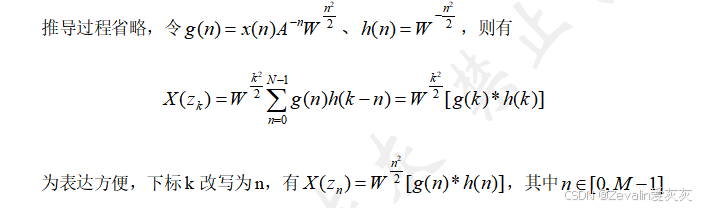
(3)CZT算法的运算框图:
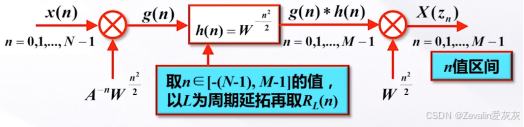
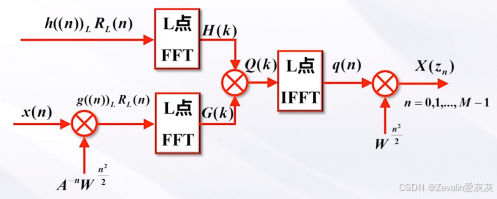
(4)用FFT实现CZT:

3、MATLAB实现CZT算法
%定义实序列h(n),此处以截止频率为0.3π的40阶低通滤波器为例
h = fir(40, 0.3);
%定义采样频率及CZT希望重点分析的频率范围,此处以1000Hz和100Hz~200Hz为例
fs = 1000; f1 = 100; f2 = 200;
%定义CZT运算长度M
m = 1024;
%定义CZT算法使用的参数
w = exp(-j*2*pi*(f2-f1)/(m*fs));
a = exp(j*2*pi*f1/fs);
%调用函数进行FFT运算和CZT运算
H = fft(h, 1000);
H1 = czt(h,m,w,a);
%横坐标转为Hz作为单位
fH = (0:length(H) - 1) * 1000 / length(H);
fH1 = (0:length(H1) - 1) * (f2 - f1) / length(H1) + f1;
%画图
figure(1); plot(fH(1:500), abs(H(1:500)));
figure(2); plot(fH1, abs(H1));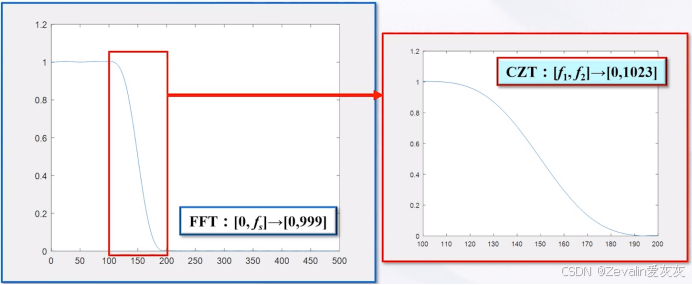






















 6934
6934

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










