数字信号处理 第三章（离散傅里叶变换）

参考教程：https://www.bilibili.com/video/BV1qTCDYpEFr?spm_id_from=333.788.videopod.sections&vd_source=8f8a7bd7765d52551c498d7eaed8acd5

一、傅里叶三种变式推导

1、傅里叶级数FS

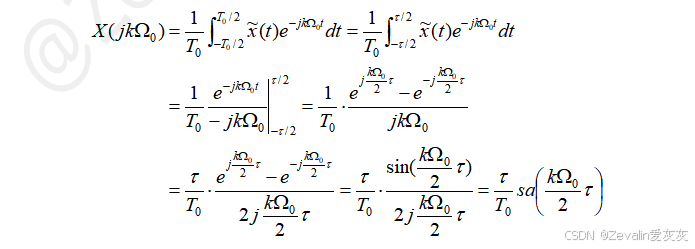
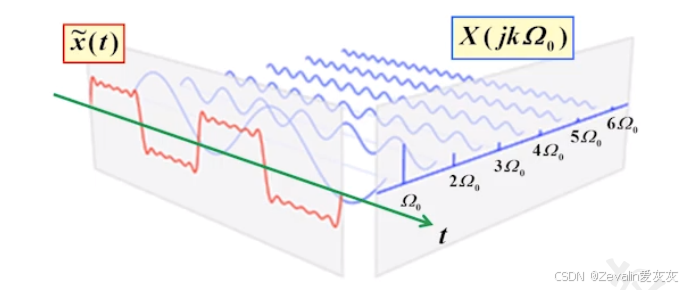
2、傅里叶变换FT

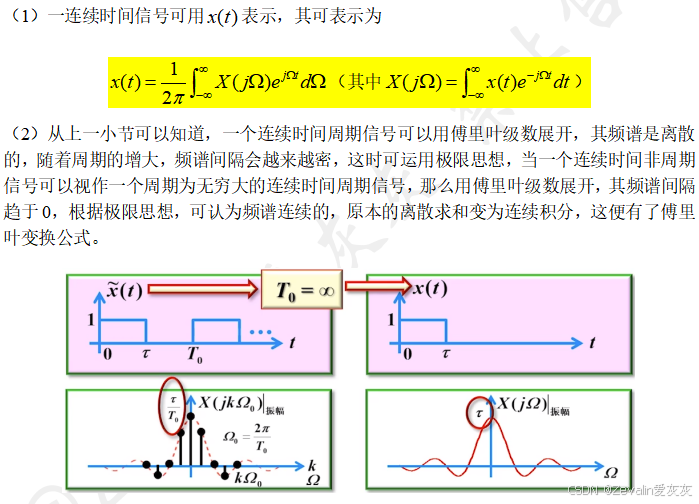
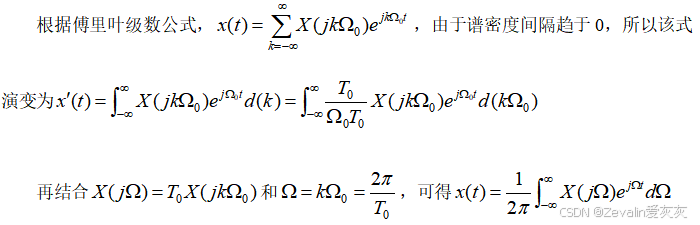
3、离散时间信号傅里叶变换DTFT

二、离散傅里叶级数及其性质

1、研究离散傅立叶级数的原因

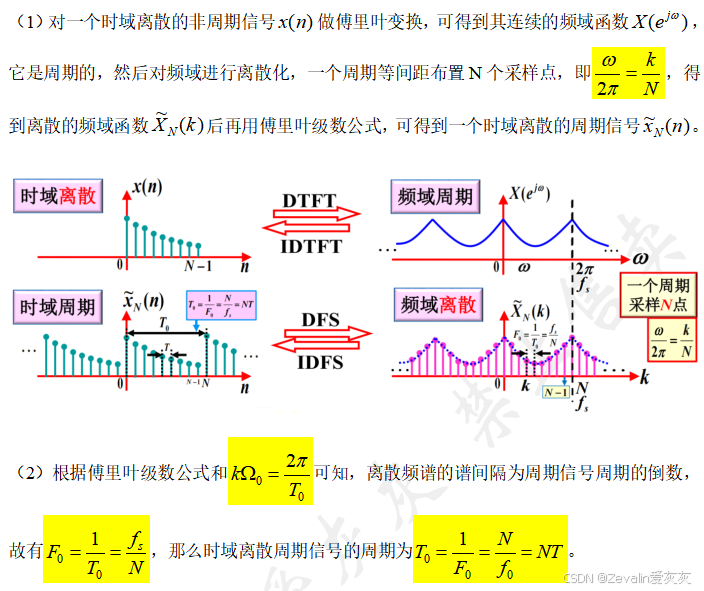
（1）前面推导了连续时间信号的傅里叶级数、傅里叶变换和离散时间的傅里叶变换，其中连续时间信号的傅里叶变换中，时域是连续的、频域是连续的，连续时间信号的傅里叶级数中，时域是连续的、频域是离散的，离散时间的傅里叶变换中，时域是离散的、频域是连续的。

（2）连续的内容在计算机中难以表达，对此需要研究离散傅里叶级数，它能做到时域和频域都是离散的。

2、由DTFT推出离散傅里叶级数DFS的表达式

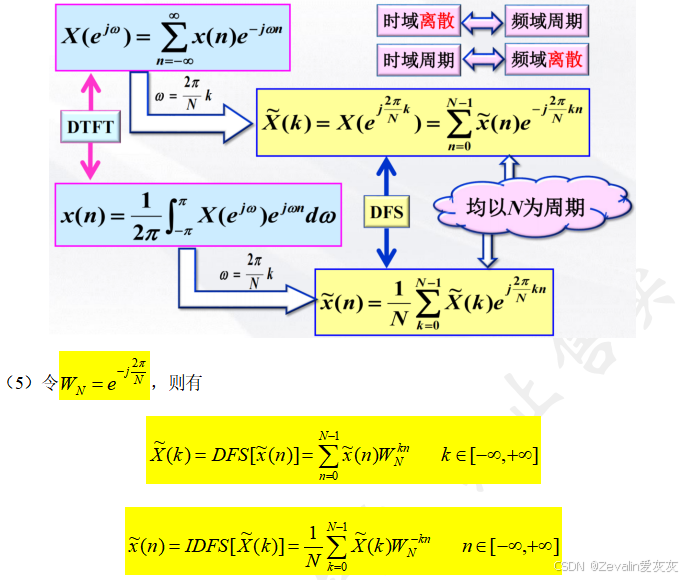
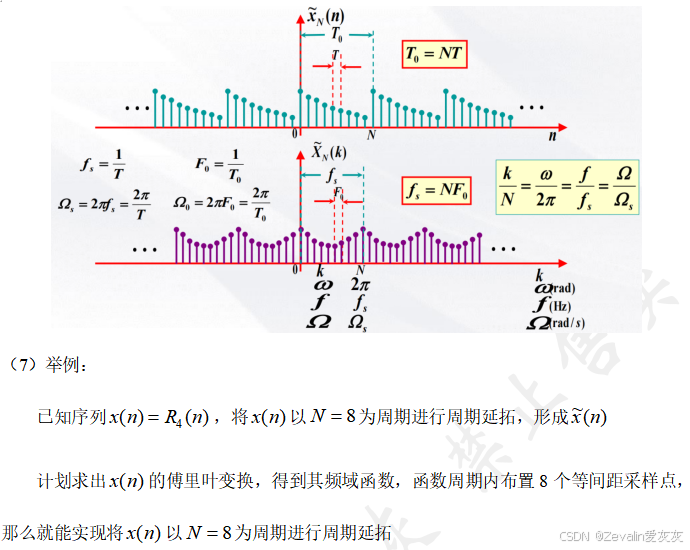
3、离散傅里叶级数的性质

（1）由于可用抽样z变换解释DFS，故DFS的许多性质与z变换相似，但与都具有周期性，所以DFS在时域和频域之间存在着严格的对偶关系，这是序列z变换所不具有的。

（2）离散傅里叶级数的几大性质：

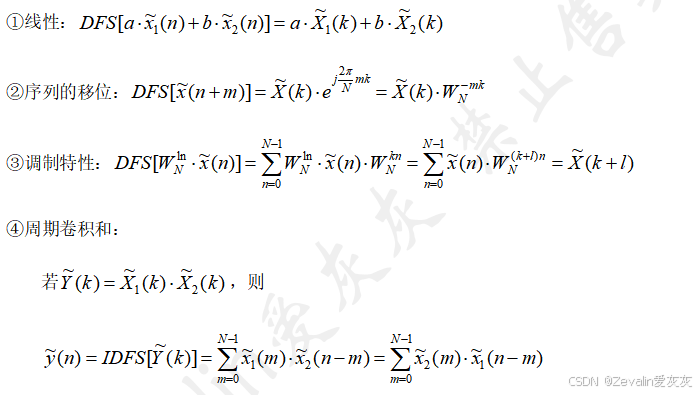
三、离散傅里叶变换的定义及其性质

1、离散傅立叶变换DFT的定义

（1）周期序列只有有限个序列值有意义，对此可以把N点有限长序列看作是周期为N的周期序列的一个周期，就可以利用离散傅立叶级数DFS来计算了。

（2）离散傅立叶变换DFT的定义引出：

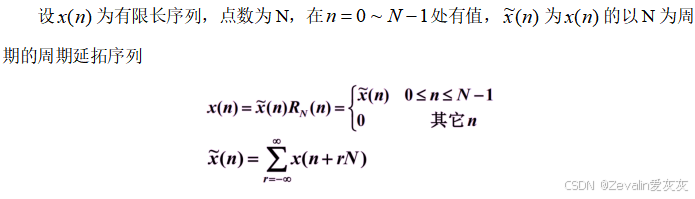
2、离散傅里叶变换隐含的周期性

（1）虽然有限长序列及其傅里叶变换的长度有限，但实际上，对它们进行周期延拓，它们之间的关系就会变成傅里叶级数展开/求和。

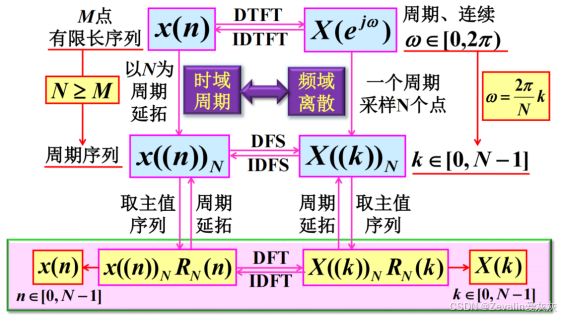
（2）回忆DFS，可以发现它们的形式基本一致，只是DFT仅考虑主值序列（有限长序列），而DFS考虑的是一个周期序列，因此，DFT的定义形式中一定会有对主值区间范围的说明。

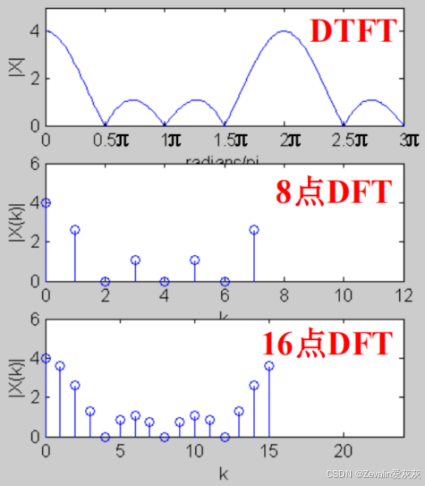
3、离散时间傅立叶变换与离散傅立叶变换的关系

（1）离散时间傅立叶变换与离散傅立叶变换的关系如下所示。

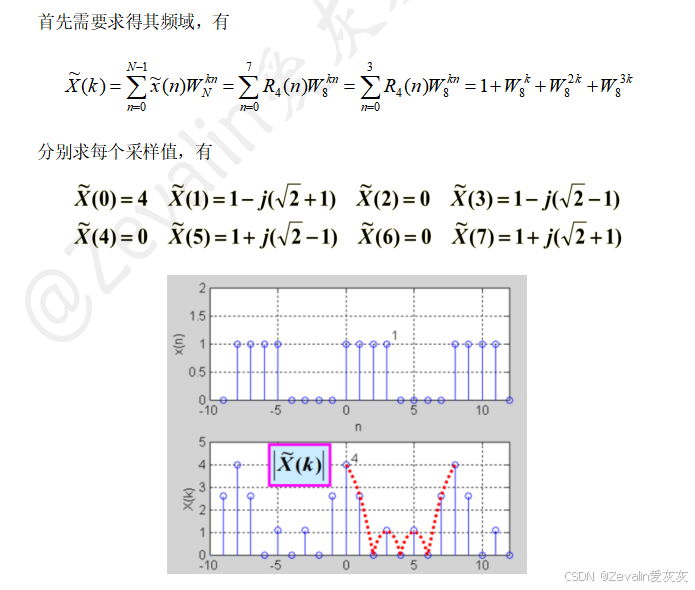
（2）举例：

4、离散傅里叶变换的基本性质

（1）线性性质：

（2）圆周（循环）移位的基本概念与实现方法：

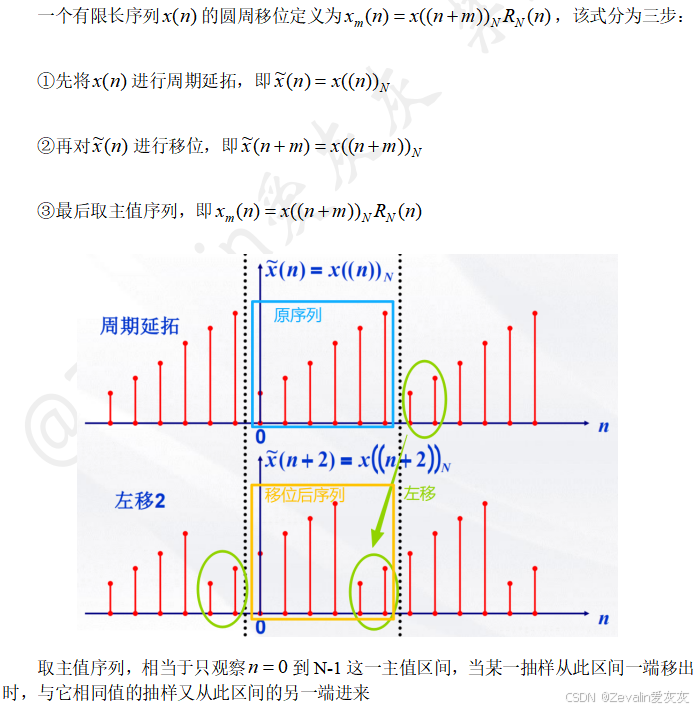
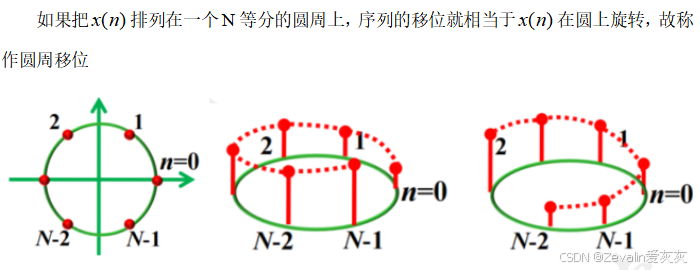
（3）时域圆周（循环）移位性质：

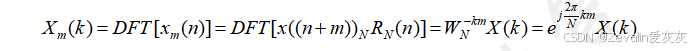
（4）频域圆周（循环）移位性质：

（5）几种常用的DFT：

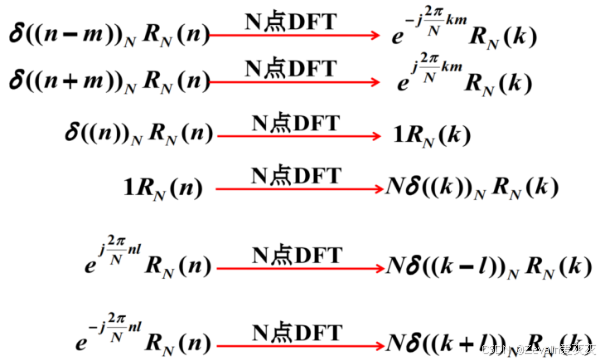
（6）举例：

5、离散傅里叶变换的共轭对称性质

（1）圆周共轭对称性质：

（2）圆周（循环）卷积性质：

四、用DFT求解LSI系统输出

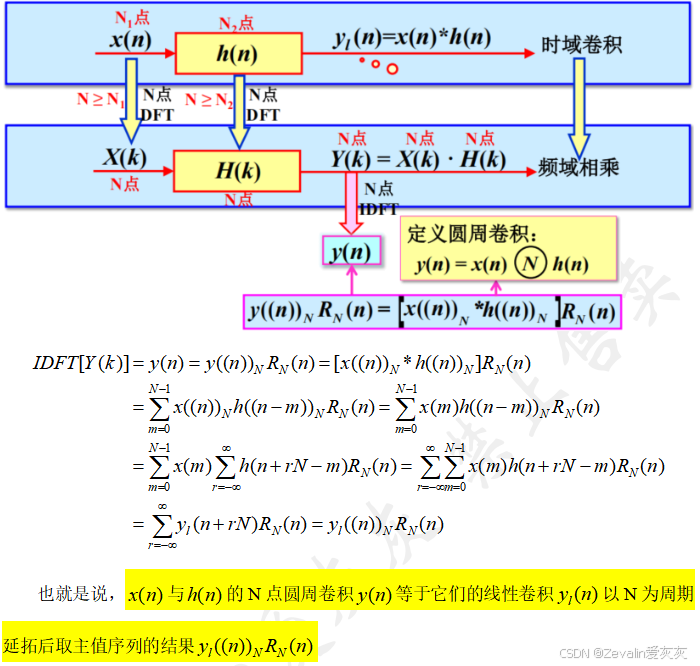
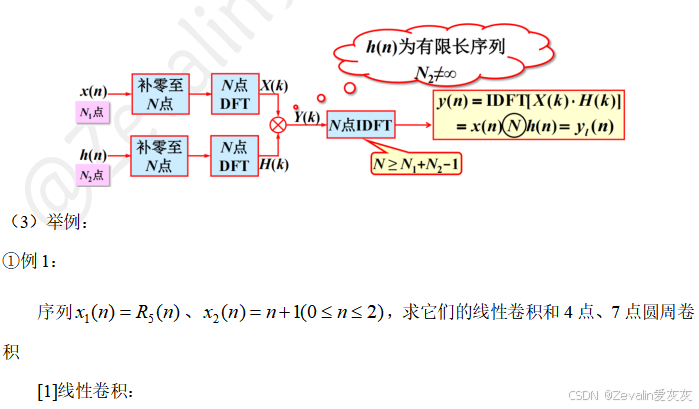
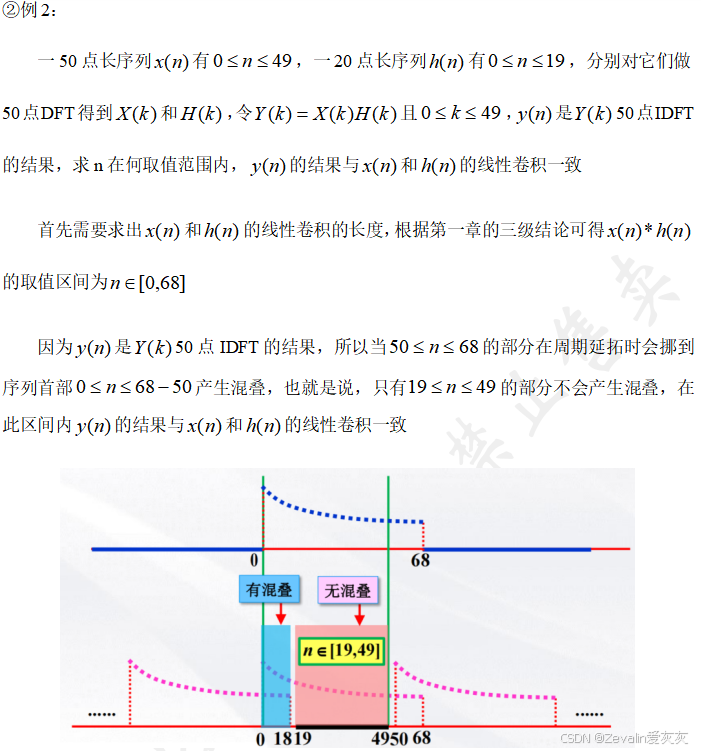
1、用DFT求解系统线性卷积输出的方法

2、长序列线性卷积的DFT求解方法——重叠相加法

（1）重叠相加法的引出：

（2）重叠相加法的基本原理：

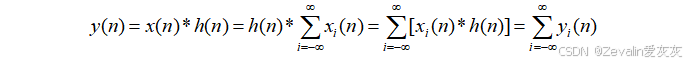
（3）的求解方法：

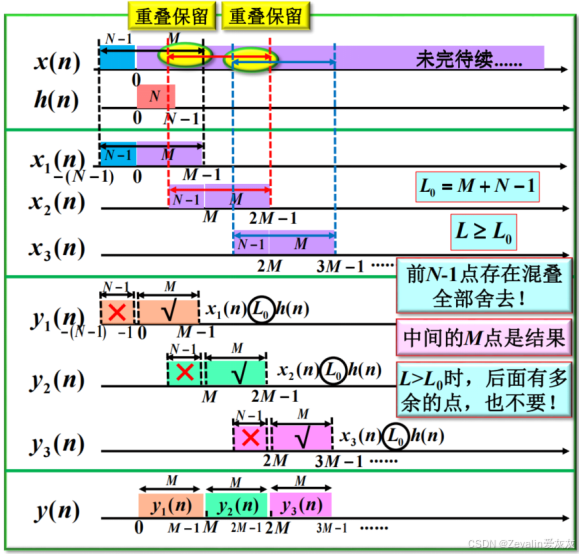
3、长序列线性卷积的DFT求解方法——重叠保留法

（1）重叠保留法的引出：

（2）重叠保留法的实现步骤：

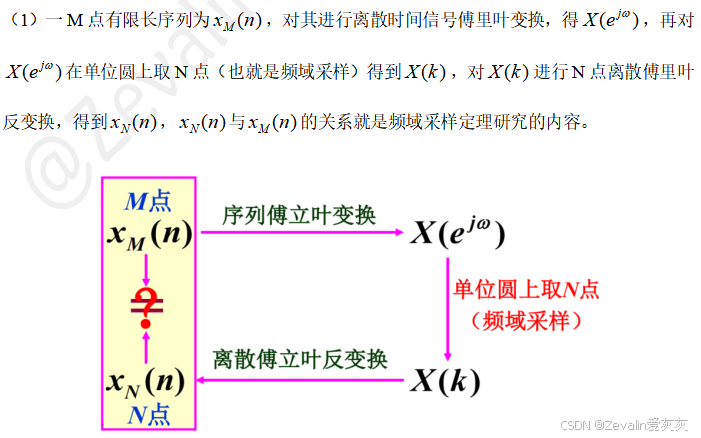
五、频域采样定理

1、频域采样与频域采样定理的引入

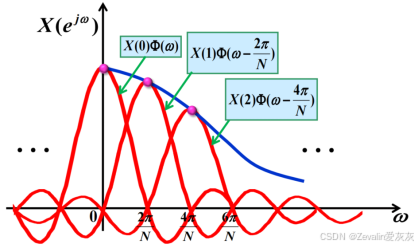
2、频域插值的恢复

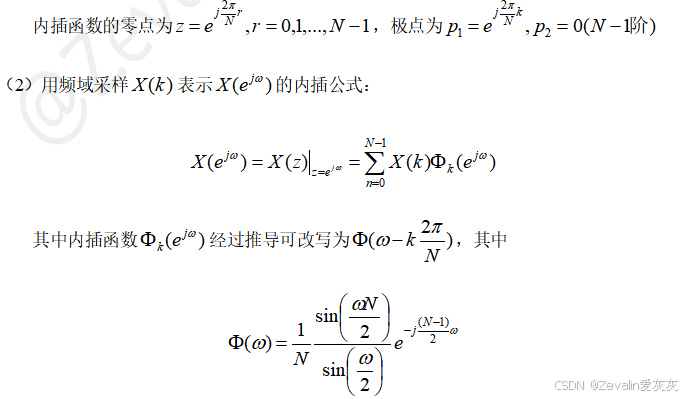
六、模拟信号的频谱分析

1、用DFT对模拟信号作频谱分析

2、谱分析方法中存在的问题及应对措施

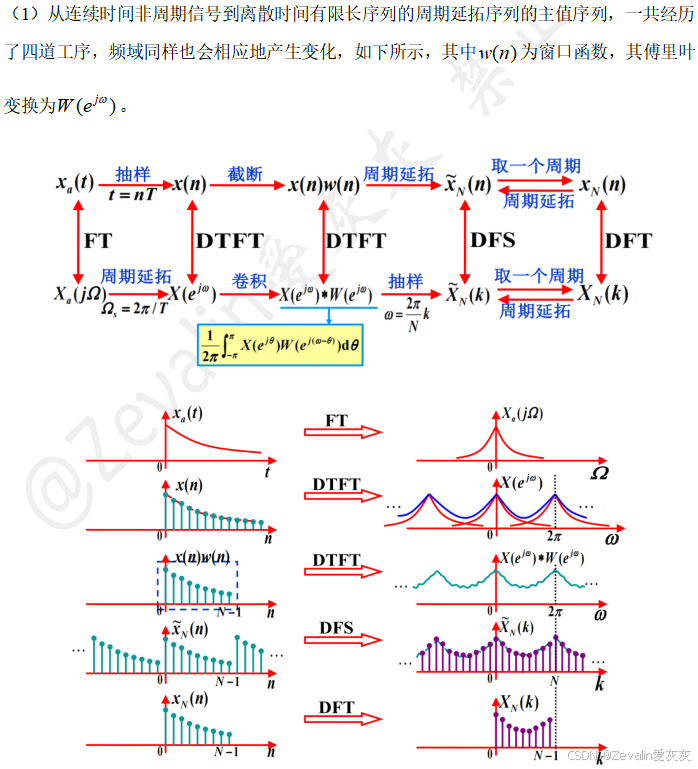
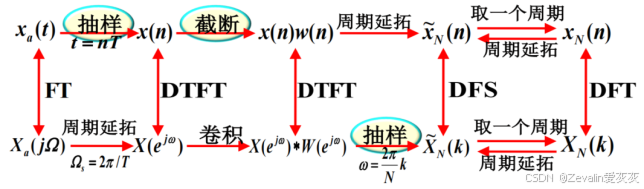
（1）上一节提到过，从连续时间非周期信号到离散时间有限长序列的周期延拓序列的主值序列，一共经历了四道工序，其中有三道工序如果处理不当（或者根本无法做到理想状态），容易对信号的细节进行破坏，如下所示。

①对连续时间信号的抽样如果不当， 比如选取的采样频率过低，会引起频域混叠。

②对抽样后的离散时间信号如果截断不当，会引起频谱泄漏。

③对截断后的离散时间信号的频域抽样如果不当，会引起栅栏效应。

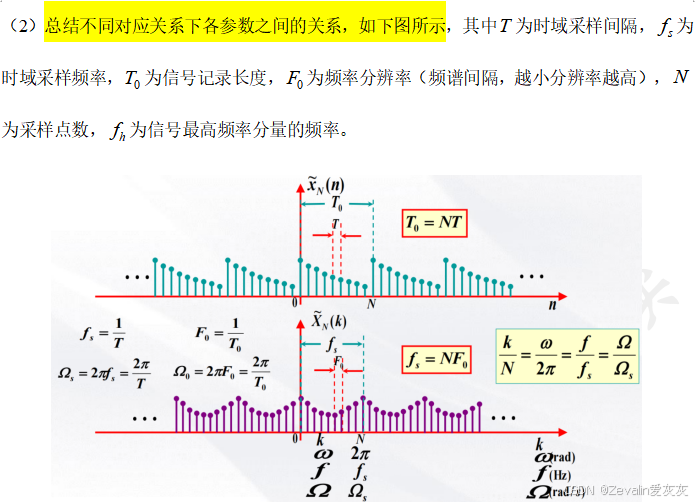
（2）时域抽样定理指出，若要从抽样后的信号中不失真的还原出原信号，则抽样频率必须大于信号最高频率分量的频率两倍以上，不过在实际中，最高频率分量的频率可能会很大，但它的幅值并不大，所以可以使用抗混叠滤波器对其进行预处理，此处不再赘述。

（3）信号的频谱与窗函数的卷积后必然产生拖尾、变宽的现象，从而造成截断效应，这就是频谱泄漏现象，所以选好窗函数非常关键。

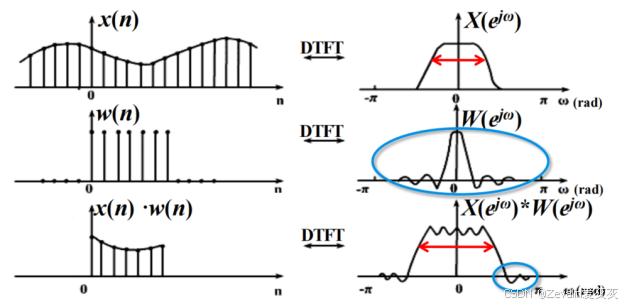
①不同窗函数及它们的频谱如下所示，增加窗函数的长度，会引起过渡带变窄，但主旁瓣能量比不变。

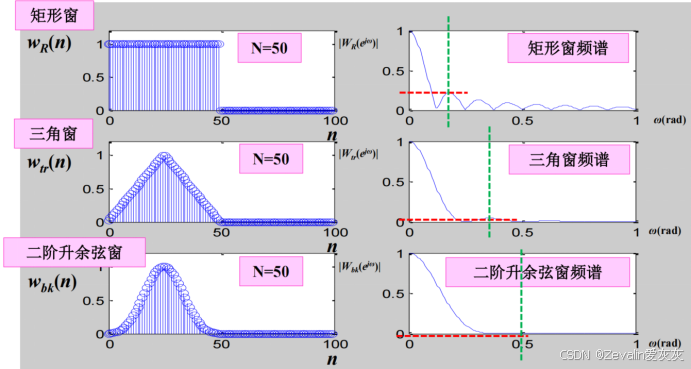
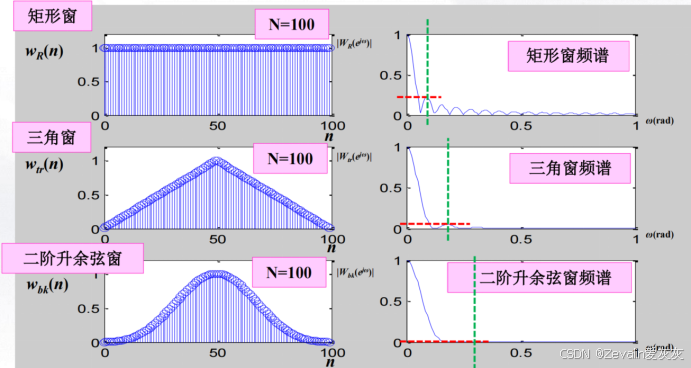
②为了减少频谱泄漏，尽可能选择时域图像形状为缓慢截断的窗函数，尽可能选择时域图像形状长度较长的窗函数。

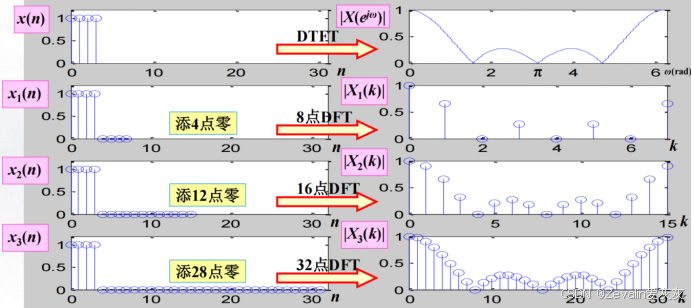
（4）对频域的抽样点增加，相应地时域上一个周期内的采样点也会增加，如下所示，可以发现，当时域中序列的末尾补的零越多，频域上的分辨率也会得到优化。