数字信号处理 第二章（z变换与LSI系统频域分析）【上】

参考教程：https://www.bilibili.com/video/BV1qTCDYpEFr?spm_id_from=333.788.videopod.sections&vd_source=8f8a7bd7765d52551c498d7eaed8acd5

一、z变换及其收敛域

1、由拉普拉斯变换到z变换

（1）z变换是离散系统与信号分析的重要工具，其地位犹如拉普拉斯变换在连续信号与系统中的地位。

（2）z变换的定义可以从理想信号（离散信号）的拉普拉斯变换引出，也可以独立地对离散信号（序列）给出其定义。

（3）从拉氏变换演变为z变换：

​

2、s平面与z平面的映射关系

​

​

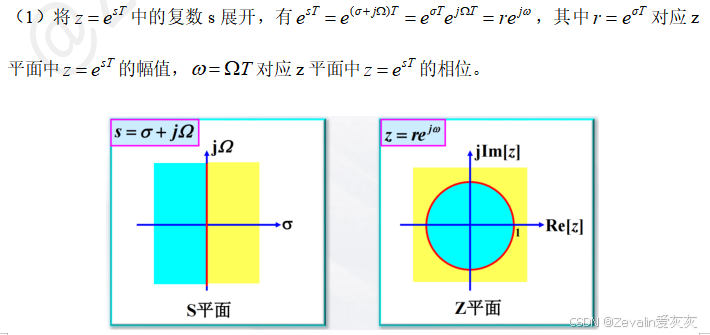
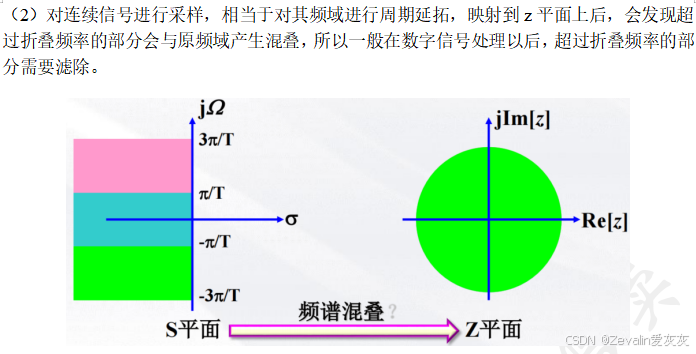
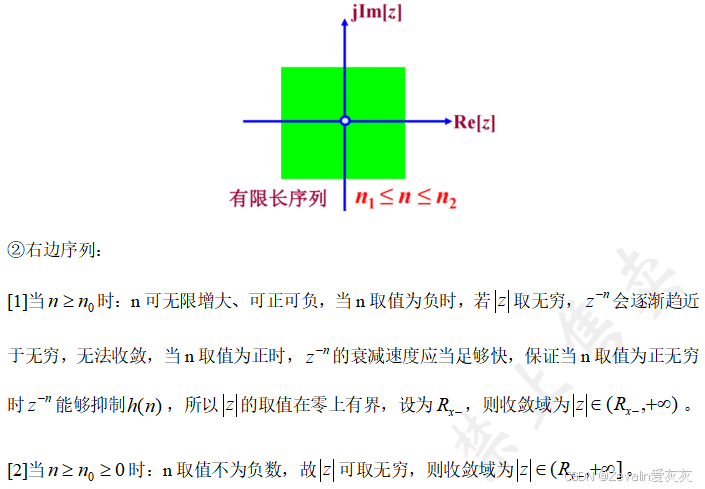
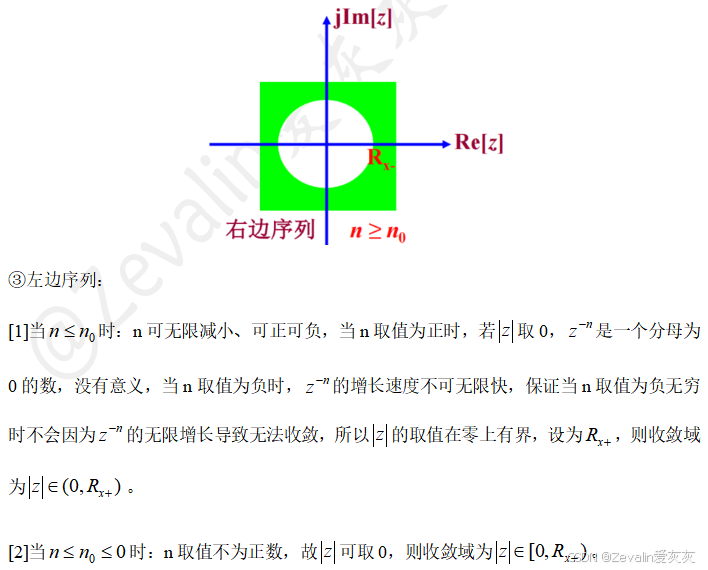
3、z变换定义及其收敛域

​

​

​

​

​

​

​

​

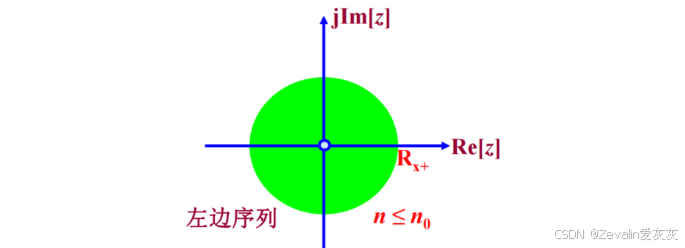
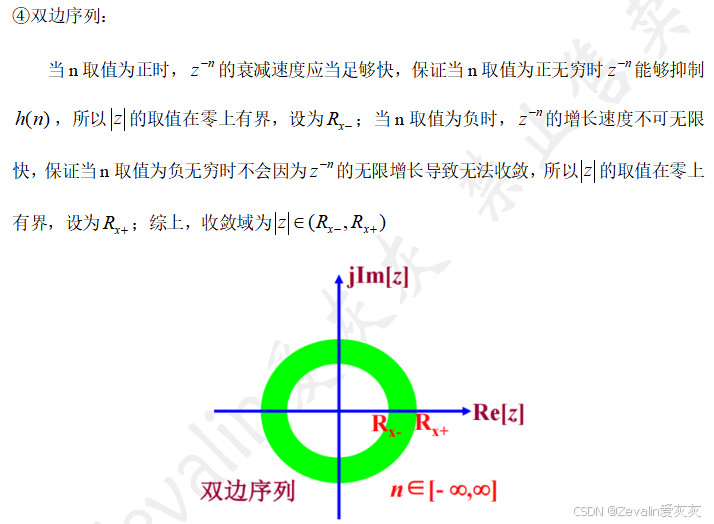
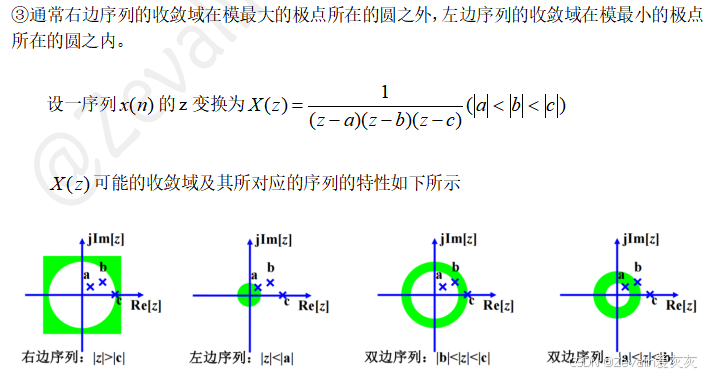
4、z反变换

（1）由求出原序列的过程称为z反变换，表示为，实际上就是求的幂级数展开式。

（2）求z反变换的三种方法：

①围线积分法（留数法）：利用复变函数中的留数定理，通过计算积分围线内极点的留数求和得到原序列，这里不进行详细介绍。

②部分分式法：将展开成部分分式的形式，然后求每个部分分式的z变换。

③幂级数展开法（长除法）：直接用的分子多项式除以分母多项式，得到。

（3）部分分式（展开）法介绍：

​

​

​

​

​

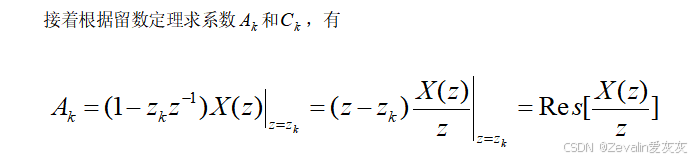
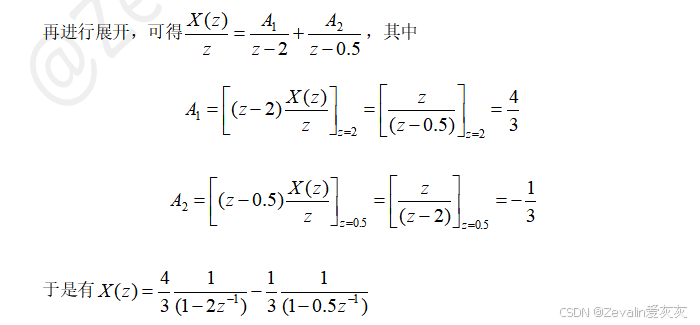
（4）幂级数展开法（长除法）介绍：

​

​

5、z变换的性质

（1）线性性质：

​

（2）移位性质：

​

（3）卷积和性质：

​

（4）z变化更多的性质如下所示，此处不过多赘述。

​

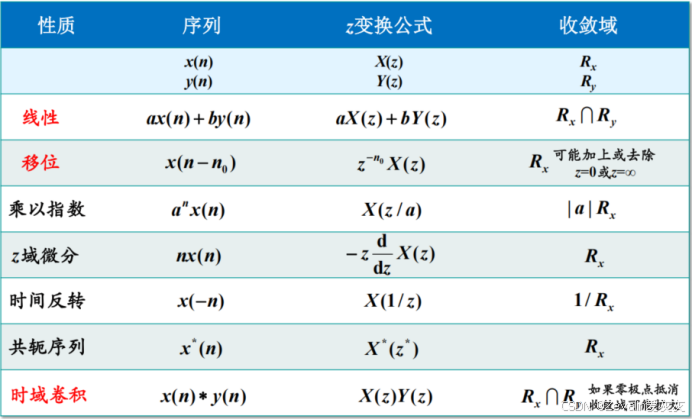
（5）举例：

​

​

二、离散时间信号的傅里叶变换

1、离散时间信号傅里叶变换的基本概念

（1）一个离散时间（非周期）信号及其频谱的关系，可以用离散时间信号（序列）的傅立叶变换（简称DTFT）来表示。

（2）DTFT正变换：

​

（3）DTFT反变换：

​

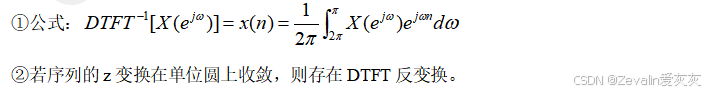
2、DTFT的共轭对称性质

（1）两个实部相等，虚部互为相反数的复数互为共轭复数，在复平面上可表示为两个点关于实轴对称。

​

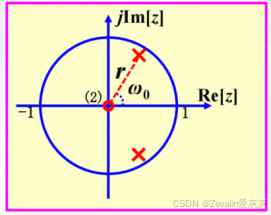
（2）共轭对称序列与共轭反对称序列的定义：

​

（3）用共轭对称序列和共轭反对称序列表示一般序列：

​

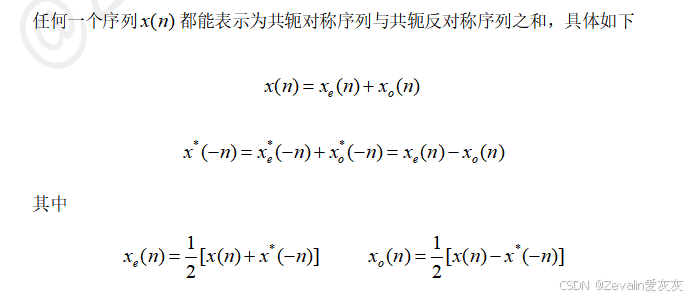
（4）关于频域函数的共轭对称性质描述：

​

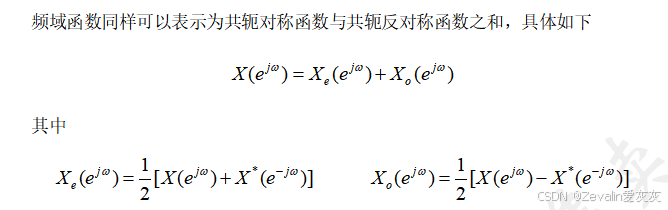
（5）时域与频域对应的共轭对称性质：

​

（6）举例：

​

​

​

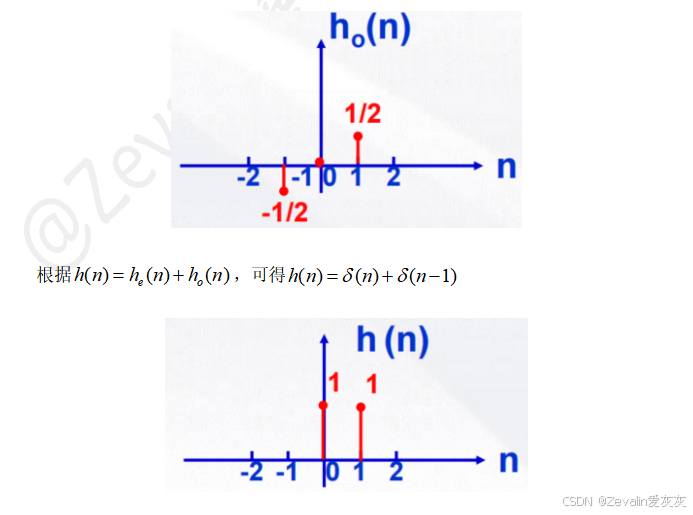
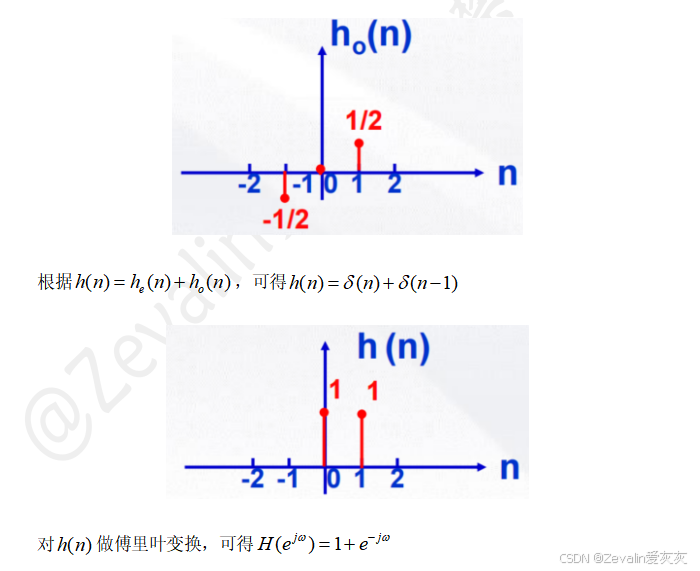
三、系统函数及其与系统性质的关系

1、由系统函数及其收敛域判断系统因果性

​

2、由系统函数及其收敛域判断系统稳定性

​

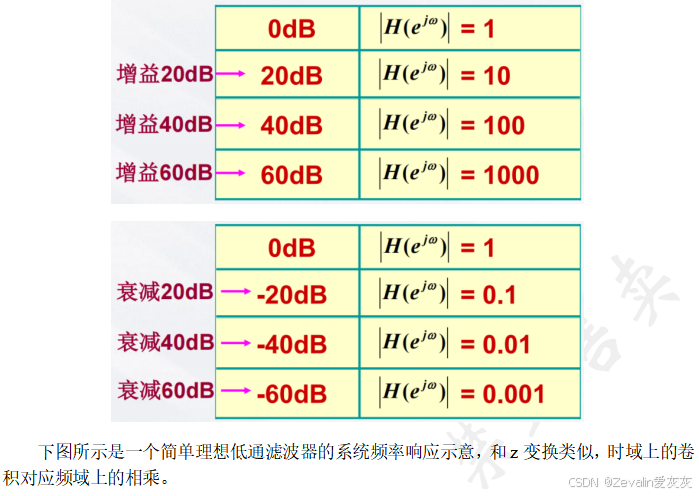
四、系统频率响应的意义

1、系统频率响应的基本概念

​

​

​

​

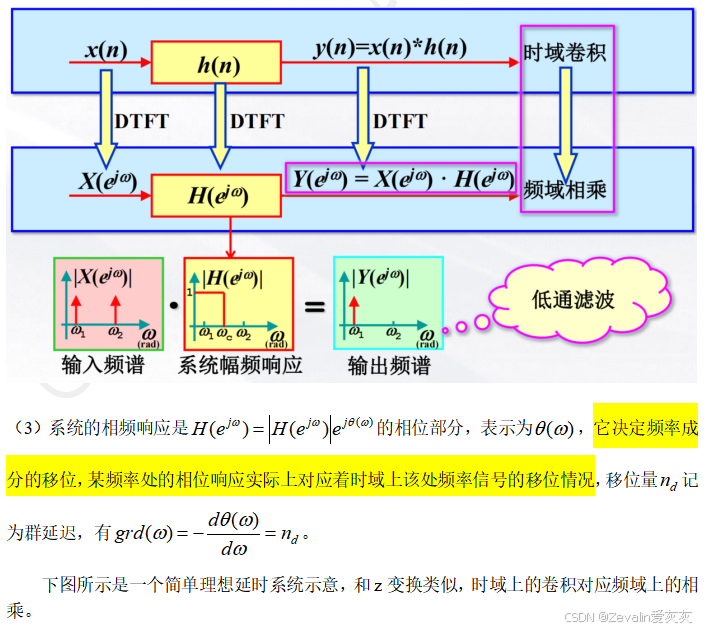
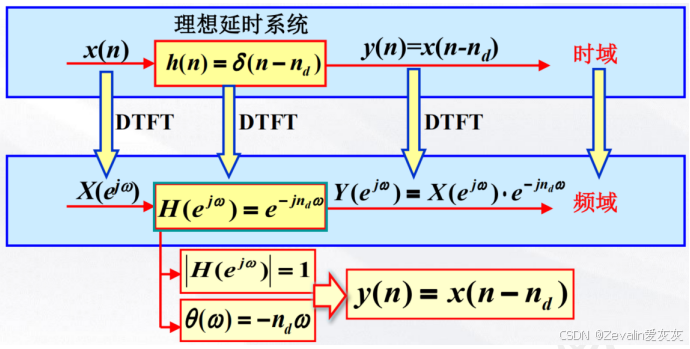
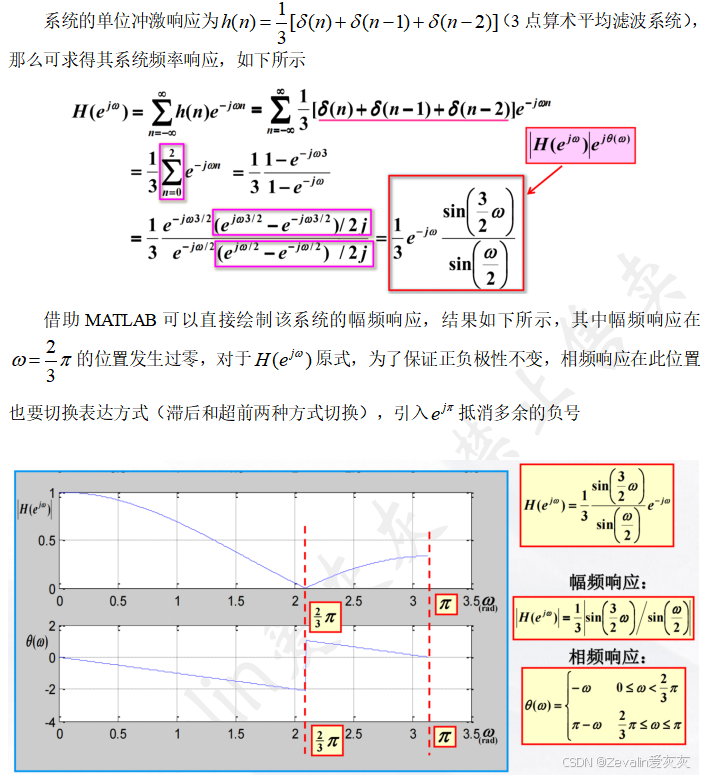
2、固定频率输入信号下的系统输出

​