【无线电控制与数据链探测系统】第7章发射源定位与追踪

发射源定位与追踪技术解析

最新推荐文章于 2025-12-03 15:06:03 发布

原创最新推荐文章于 2025-12-03 15:06:03 发布 · 890 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #矩阵 #概率论

本章系统推导基于到达时间（TOA/TDOA）、到达角（AOA）与接收信号强度（RSS）的定位原理，严格分析各类误差来源并给出几何与统计推导。基于这些测量构建的多站协同定位、基于随机动态模型的跟踪滤波（卡尔曼、粒子滤波）与多假设/多目标关联方法也给出完整推导与实现细节。被动定位中的时钟同步问题、时延估计精度的 Cramér–Rao 下界（CRLB）推导以及移动目标的轨迹拼接与多站关联规则均在本章以教材级别的完整步骤展开。

7.1 TOA/TDOA、AOA、RSS 原理与误差来源（含几何推导）

7.1.1 基本几何模型与符号

7.1.2 TOA / TDOA 的几何推导与線性化解法

求解方程组的直接非线性方法或通过线性化（Taylor expansion）导出迭代最小二乘（Gauss–Newton）解。

以 TOA（已知发射时刻或同步接收）为例，测量方程（去掉常数）：

7.1.3 AOA 的阵列与角度估计（包括 MUSIC 的推导）

7.1.4 RSS 定位的统计推导

7.1.5 误差来源与几何因子（GDOP）

7.2 多站协同定位与数据融合（卡尔曼滤波、粒子滤波实现细节）

7.2.1 动态定位的状态空间建模

7.2.2 卡尔曼滤波（线性-Gaussian 最优滤波器）推导

7.2.3 扩展卡尔曼滤波（EKF）与无迹卡尔曼滤波（UKF）

7.2.4 粒子滤波（Sequential Monte Carlo）详解与伪码

输入: N_particles, initial particles {x_k^{(i)}}_{i=1}^N ~ p(x_0), weights w^{(i)}=1/N
for each time k:
   1. 预测: for i=1..N: x_{k|k-1}^{(i)} ~ p(x_k | x_{k-1}^{(i)})
   2. 重要性权重: w_k^{(i)} ∝ w_{k-1}^{(i)} * p(z_k | x_{k|k-1}^{(i)})
   3. 归一化权重: w_k^{(i)} = w_k^{(i)} / sum_j w_k^{(j)}
   4. 计算有效粒子数: N_eff = 1 / sum_i (w_k^{(i)})^2
   5. 若 N_eff < threshold: 重采样 (systematic/residual) 得均匀权重后置
   6. 输出估计: e.g., \hat{x}_k = sum_i w_k^{(i)} x_{k|k-1}^{(i)}

细节与实现要点：

7.2.5 多站协同数据融合架构

7.3 被动定位系统设计（时钟同步、时延估计精度分析）

7.3.1 时钟同步：双向时间传输的数学解法

被动系统的接收站若无全局 GPS 等同步手段，可采用两站间的双向时间传输（Two-Way Time Transfer, TWTT）来估计时钟偏差与传播延迟。两站 A 与 B 交换时间戳并记录发送/接收时间：

若考虑非对称延迟与丢包，则需采用更复杂的统计估计（最小二乘或最大似然）并在协议层做可靠传输保障。

7.3.2 时延估计的精度（CRLB）推导

7.3.3 采样、量化与相关峰值定位误差

7.4 移动目标追踪与跨站关联（多假设追踪、轨迹拼接）

7.4.1 目标运动模型与滤波器的选择

7.4.2 数据关联：Gating、JPDA 与 MHT

JPDA（Joint Probabilistic Data Association）：针对每轨迹在每时刻计算测量归属的概率（考虑门控集合内的所有可能测量），并将所有测量以加权方式更新滤波器，避免硬分配导致的误关联。JPDA 的权重计算基于测量到轨迹的似然比并包含虚警率与漏检概率参数。

MHT（Multi-Hypothesis Tracking）：维护关联假设树，延迟决策以考虑多时刻的数据。MHT 的基本思想是在事件不确定时保持多个可能的关联路径并随着时间推进和新测量到来逐步剔除低概率假设。伪码（高层）：

初始化: 空假设树
for each time k:
   1. 生成所有可能的测量-轨迹关联组合（受门控限制）
   2. 对每个假设计算似然并更新轨迹状态与权重
   3. 合并同质假设并修剪低权重假设以控制指数增长
   4. 输出高权重轨迹与其概率

MHT 给出近似最优的数据关联但计算复杂度高，通常结合启发式剪枝与窗口化策略。

7.4.3 轨迹拼接（跨站 / 跨段关联）

在分布式观测场景下，单站或子网可能对同一目标获得片段轨迹，需在时空上拼接成完整轨迹。拼接的核心为度量两个轨迹段在时间交接处的相容性，包括位置、速度与加速度的一致性及轨迹段间时间重叠/间隔的合理性。可构造拼接代价函数

在阈值下选择最小代价配对（匈牙利算法用于多对多最优匹配），或者把拼接作为 MHT 的一部分处理时间间隔。

7.4.4 平滑与后验轨迹优化（Rauch–Tung–Striebel 平滑）

得到滤波器在线估计后，可以用平滑算法获得更好的后验轨迹（利用未来观测信息）。Rauch–Tung–Striebel (RTS) 平滑为线性高斯模型的最优固定间隔平滑器：

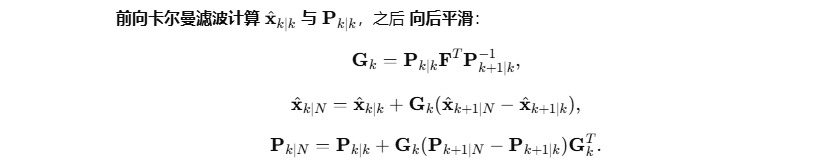
RTS 平滑可显著降低轨迹抖动并改进位置精度（使用全段观测）。

7.5 本章小结与工程实践要点

TOA/TDOA/AOA/RSS 各有优缺点：TOA（需发射时刻或接收同步）、TDOA（可消除发射时刻但需站间同步）、AOA（阵列硬件复杂但在几何好时精度高）、RSS（实现简单但精度低）。
定位问题本质为非线性最小二乘或最大似然问题，常用线性化（Gauss–Newton）、代数闭式解（在特殊几何下）或数值优化求解。
定位精度的根本限制来自时延估计的 CRLB，CRLB 与信号带宽与 SNR 成正比——宽带系统对精度的提升具有理论支持。
多站协同与动态跟踪通过状态空间模型（卡尔曼、EKF、UKF、PF）在不同非线性与噪声假设下提供可行的滤波器选择；数据关联问题（JPDA、MHT）是多目标跟踪的核心挑战。
被动系统的时钟同步与测量延迟估计至关重要，双向时间传输与网络时钟同步算法为工程实现提供可行路径。
在工程实现中必须把几何 GDOP、NLOS 偏差与多路径、采样定时抖动、ADC/量化误差、时钟相位噪声等系统性误差建模到估计流程中，通过模型校正、鲁棒滤波（如 Huber 损失）、和数据驱动（机器学习/统计）方法减轻偏差影响。