线代强化NO11|线性方程组|解的判定|齐次线性方程组解的结构|非齐次线性方程组的解的结构

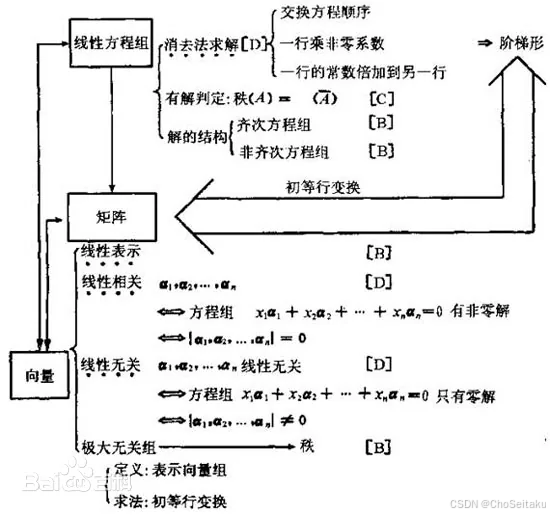
解的判定

基本概念

1. 线性方程组
   $$\begin{array}{rl}& \text{方程组}\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \cdots \cdots \cdots \cdots \\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=b_m\end{array}\text{称为}m\text{个方程，}n\text{个未知量的线性方程组。}\\ & \text{其中}{x}_1,x_2,\cdots ,x_n\text{为未知数，}m\text{为方程的个数，}{b}_1,b_2,\cdots ,b_m\text{为常数项。}\\ & \text{如果常数项}{b}_1=b_2=\cdots =b_m=0\text{，则称该方程组为齐次线性方程组。相反地，如果}\\ & b_1,b_2,\cdots ,b_m\text{不全为零，则称该方程组为非齐次线性方程组，将任一非齐次线性方程组}\\ & \text{的常数项改为零所得到的齐次线性方程组称为原方程组的导出组。}\end{array}$$
2. 线性方程组的矩阵
   $$\begin{array}{rl}& \text{由线性方程组}\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \cdots \cdots \cdots \cdots \\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=b_m\end{array}\text{的系数构成的}m\times n\text{矩阵}\\ & A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]\text{称为该线性方程组的系数矩阵。}\\ & \text{和常数项构成的}m\times (n+1)\text{矩阵}\overline{A}=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& \cdots & a_{1n}& b_1\\ a_{21}& a_{22}& \cdots & a_{2n}& b_2\\ ⋮& ⋮& & ⋮& ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}& b_m\end{array}\right]\text{称为该线性方程组的增广矩阵。}\\ & \text{如果令}\boxed{x}=[x_1,x_2,\cdots ,x_n{]}^T,\boxed{b}=[b_1,b_2,\cdots ,b_m{]}^T\text{，利用矩阵的乘法，我们可以将原线性}\\ & \text{方程组简写为}A\boxed{x}=\boxed{b}\text{。}\end{array}$$
3. 高斯消元法
   $$\begin{array}{rl}& \text{①线性方程组的初等变换}\\ & \text{我们对线性方程组可以作如下的三种变换：}\\ & \text{1)将一个非零常数}k\text{乘到方程的两端；}\\ & \text{2)将一个方程的}k\text{倍加到另一个方程上；}\\ & \text{3)交换两个方程的位置。}\\ & \text{我们将线性方程组的这三种变换称之为线性方程组的初等变换。对线性方程组做初等}\\ & \text{变换得到的新的线性方程组与原来的线性方程组是同解的。易知，对线性方程组做初等}\\ & \text{变换等价于对其增广矩阵做相应的初等行变换。}\\ & \text{【注】由于齐次线性方程组的常数项恒为零，我们在对其做初等变换时只需对它的系}\\ & \text{数矩阵做相应的初等行变换。}\end{array}$$
   $$\begin{array}{rl}& \text{②高斯消元法}\\ & \text{我们对线性方程组作初等变换的目的是为了将其化为与之同解的如下形式的线性方程组：}\\ & \{\begin{array}{l}{a}_{11}^{\prime }{x}_1+a_{12}^{\prime }{x}_2+a_{13}^{\prime }{x}_3+\cdots +a_{1n}^{\prime }{x}_n=b_1^{\prime }\\ a_{22}^{\prime }{x}_2+a_{23}^{\prime }{x}_3+\cdots +a_{2n}^{\prime }{x}_n=b_2^{\prime }\\ a_{33}^{\prime }{x}_3+\cdots +a_{3n}^{\prime }{x}_n=b_3^{\prime }\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ a_{kk}^{\prime }{x}_k+\cdots +a_{kn}^{\prime }{x}_n=b_k^{\prime }\end{array}\\ & \text{在该方程组中，每一个方程都至少比上一个方程少一个未知量，这种方程组称为阶梯}\\ & \text{形方程组。在阶梯形方程组中，每一行的第一个未知量称为主元，其余的未知量称为}\\ & \text{自由变量。阶梯形方程组的解是比较容易求得的。将线性方程组通过初等变换化为同}\\ & \text{解的阶梯形方程组的过程就称之为高斯消元法。}\\ & \text{易知，利用高斯消元法求解线性方程组就等价于利用初等行变换将线性方程组的矩阵化}\\ & \text{为阶梯形矩阵。}\end{array}$$
   $$\begin{array}{rl}& \text{【注】①高斯消元法示例：}\\ & \{\begin{array}{l}{x}_1+x_2+x_3=3\\ x_1+2x_2+4x_3=7\\ x_1+3x_2+9x_3=13\end{array}\to \{\begin{array}{l}{x}_1+x_2+x_3=3\\ x_2+3x_3=4\\ 2x_2+8x_3=10\end{array}\to \{\begin{array}{l}{x}_1+x_2+x_3=3\\ x_2+3x_3=4\\ x_2+4x_3=5\end{array}\to \{\begin{array}{l}{x}_1+x_2+x_3=3\\ x_2+3x_3=4\\ x_3=1\end{array}\\ & \text{从最后一个线性方程组中不难求出原线性方程组的解为}\{\begin{array}{l}{x}_1=1\\ x_2=1\\ x_3=1\end{array}\\ & \text{②高斯消元法的矩阵形式}\\ & \text{对上述的线性方程组，其求解过程等价于对其增广矩阵作如下的变换：}\\ & \left[\begin{array}{cccc}1& 1& 1& 3\\ 1& 2& 4& 7\\ 1& 3& 9& 13\end{array}\right]\to \left[\begin{array}{cccc}1& 1& 1& 3\\ 0& 1& 3& 4\\ 0& 2& 8& 10\end{array}\right]\to \left[\begin{array}{cccc}1& 1& 1& 3\\ 0& 1& 3& 4\\ 0& 1& 4& 5\end{array}\right]\to \left[\begin{array}{cccc}1& 1& 1& 3\\ 0& 1& 3& 4\\ 0& 0& 1& 1\end{array}\right]\\ & \text{再将最后的增广矩阵还原为线性方程组同样可以求出原方程组的解。}\end{array}$$

解的判定

1. 线性方程组解的存在性
   $$\begin{array}{rl}& \text{定理 1：设}A=[{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n]\text{，其中}{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n\text{为}A\text{的列向量，则线性方程组}\\ & A\boxed{x}=\boxed{b}\text{有解}\\ & \iff \text{向量}\boxed{b}\text{能由向量组}{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n\text{线性表示；}\\ & \iff \text{向量组}{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n\text{与向量组}{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n,\boxed{b}\text{等价；}\\ & \iff r({\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n)=r({\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n,\boxed{b})；\\ & \iff r(A)=r(A,\boxed{b})；\end{array}$$
2. 线性方程组解的唯一性
   $$\begin{array}{rl}& \text{定理 2：当线性方程组}A\boxed{x}=\boxed{b}\text{有解时，}A\boxed{x}=\boxed{b}\text{的解不唯一（有无穷多解）}\\ & \iff \text{线性方程组的导出组}A\boxed{x}=\boxed{0}\text{有非零解；}\\ & \iff \boxed{b}\text{由向量组}{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n\text{线性表示的方式不唯一；}\\ & \iff \text{向量组}{\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n\text{线性相关；}\\ & \iff r({\boxed{\alpha }}_1,{\boxed{\alpha }}_2,\cdots ,{\boxed{\alpha }}_n)<n；\\ & \iff r(A)<n。\\ & \text{推论：设}A\text{为}m\times n\text{矩阵，当}m<n\text{时，}A\boxed{x}=\boxed{0}\text{必有非零解。}\end{array}$$
3. 克莱姆法则
   $$\begin{array}{rl}& \text{设}A\text{为}n\text{阶矩阵，则线性方程组}A\boxed{x}=\boxed{b}\text{有唯一解的充要条件是}|A|\ne 0\text{。并且唯一解为：}\\ & x_i=\frac{D_i}{D}\text{，其中}D=|A|,D_i\text{等于将}A\text{的第}i\text{列换成}\boxed{b}\text{之后所得矩阵的行列式。}\\ & \text{推论：}A\text{为}n\text{阶矩阵时，}A\boxed{x}=\boxed{0}\text{有非零解的充要条件是}|A|=0\text{。}\end{array}$$

齐次线性方程组解的结构

解的性质

$$\begin{array}{rl}& \text{定理：如果}{\boxed{\eta }}_1,{\boxed{\eta }}_2\text{为齐次线性方程组}A\boxed{x}=\boxed{0}\text{的两个解，则对任意的常数}{k}_1,k_2,\\ & k_1{\boxed{\eta }}_1+k_2{\boxed{\eta }}_2\text{仍为}A\boxed{x}=\boxed{0}\text{的解。}\\ & \text{【注】（1）该定理也可以概括为}{\boxed{\eta }}_1,{\boxed{\eta }}_2\text{的任意线性组合仍为}A\boxed{x}=\boxed{0}\text{的解；}\\ & \text{（2）该定理还可以推广到多个向量的情况：假设}{\boxed{\eta }}_1,{\boxed{\eta }}_2,\cdots ,{\boxed{\eta }}_k\text{是}A\boxed{x}=\boxed{0}\text{的解，则}\\ & {\boxed{\eta }}_1,{\boxed{\eta }}_2,\cdots ,{\boxed{\eta }}_k\text{的任意线性组合仍为}A\boxed{x}=\boxed{0}\text{的解。}\end{array}$$

基础解系

1. 基本概念
   $$\begin{array}{rl}& \text{假设齐次线性方程组}A\boxed{x}=\boxed{0}\text{有非零解。向量组}{\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s\text{称为齐次线性方程组}\\ & A\boxed{x}=\boxed{0}\text{的一个基础解系，如果它们满足如下三个条件：}\\ & \text{①}{\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s\text{都是}A\boxed{x}=\boxed{0}\text{的解；}\\ & \text{②}{\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s\text{线性无关；}\\ & \text{③}A\boxed{x}=\boxed{0}\text{的任意解都可以由}{\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s\text{线性表示。}\\ & \text{如果}{\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s\text{为}A\boxed{x}=\boxed{0}\text{的基础解系，则}A\boxed{x}=\boxed{0}\text{的通解可以表示为}\\ & k_1{\boxed{\xi }}_1+k_2{\boxed{\xi }}_2+\cdots +k_s{\boxed{\xi }}_s(k_1,k_2,\cdots ,k_s\in R)。\end{array}$$
   $$\begin{array}{rl}& \text{【注】基础解系是求齐次和非齐次线性方程组通解的关键，是解的结构部分最重要的}\\ & \text{概念，为了让考生对该概念有正确而全面的认识，我们从如下两方面来予以说明：}\\ & \text{①齐次线性方程组}A\boxed{x}=\boxed{0}\text{的基础解系}{\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s\text{是}A\boxed{x}=\boxed{0}\text{的一组线性无关的解，}\\ & \text{它们可以线性表示}A\boxed{x}=\boxed{0}\text{的任意解。也就是说，假设}\boxed{\alpha }\text{是}A\boxed{x}=\boxed{0}\text{的任一解，向量组}\\ & {\boxed{\xi }}_1,{\boxed{\xi }}_2,\cdots ,{\boxed{\xi }}_s,\boxed{\alpha }\text{是线性相关的。通过上述分析不难发现，基础解系本质上是齐次线性方}\\ & \text{程组解集的一个极大线性无关组。}\\ & \text{②由于基础解系就是极大线性无关组，那么极大线性无关组的性质对基础解系同样}\\ & \text{成立，如：齐次线性方程组的任意两个基础解系是等价的，齐次线性方程组的任意两个}\\ & \text{基础解系所含的向量个数相等。}\end{array}$$
2. 核心定理
   $$\begin{array}{rl}& \text{定理：设齐次线性方程组}{A}_{m\times n}\boxed{x}=\boxed{0}\text{（}m\text{个方程，}n\text{个未知量）系数矩阵}A\text{的秩}\\ & r(A)<n\text{，则齐次线性方程组}A\boxed{x}=\boxed{0}\text{的基础解系存在，并且任一个基础解系中含有}\\ & n-r(A)\text{个解向量。}\\ & \text{【注】①结合对基础解系定义的说明，该定理实质上是说齐次线性方程组}A\boxed{x}=\boxed{0}\text{的解}\\ & \text{集的秩为}n-r(A)\text{；}\\ & \text{②由极大线性无关组的性质还可以得到：}A\boxed{x}=\boxed{0}\text{的任意}n-r(A)\text{个线性无关的解都是}\\ & A\boxed{x}=\boxed{0}\text{的一个基础解系。}\end{array}$$
3. 计算方法
   $$\begin{array}{rl}& \text{①设}r(A)=r<n\text{，则对系数矩阵}A\text{实施初等行变换化为阶梯形矩阵。找出主元}\\ & \text{（每行第一个非零元），再进一步通过初等行变换将方程组化为“行最简形”（使得}\\ & \text{主元所在列成为一个单位矩阵）。我们给出了主元为前}r\text{个变量的情形，如下：}\\ & \left[\begin{array}{ccccccc}1& 0& \cdots & 0& {\overline{a}}_{1(r+1)}& \cdots & {\overline{a}}_{1n}\\ 0& 1& \cdots & 0& {\overline{a}}_{2(r+1)}& \cdots & {\overline{a}}_{2n}\\ ⋮& ⋮& & ⋮& ⋮& & ⋮\\ 0& 0& \cdots & 1& {\overline{a}}_{r(r+1)}& \cdots & {\overline{a}}_{rn}\\ 0& 0& \cdots & 0& 0& \cdots & 0\\ 0& 0& \cdots & 0& 0& \cdots & 0\end{array}\right]\end{array}$$
   $$\begin{array}{rl}& \text{②则对应的齐次线性方程组可化为如下形式：}\\ & \{\begin{array}{l}{x}_1+{\overline{a}}_{1(r+1)}{x}_{r+1}+\cdots +{\overline{a}}_{1n}{x}_n=0\\ x_2+{\overline{a}}_{2(r+1)}{x}_{r+1}+\cdots +{\overline{a}}_{2n}{x}_n=0\\ \cdots \cdots \\ x_r+{\overline{a}}_{r(r+1)}{x}_{r+1}+\cdots +{\overline{a}}_{rn}{x}_n=0\end{array}\\ & \text{③在上述方程中，分别令“自由变量”（主元以外的变量）其中一个为1，其余为0，}\\ & \text{如下：}\\ & \left[\begin{array}{c}{x}_{r+1}\\ x_{r+2}\\ ⋮\\ x_n\end{array}\right]=\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\\ ⋮\\ 0\end{array}\right],\cdots ,\left[\begin{array}{c}0\\ 0\\ ⋮\\ 1\end{array}\right]\\ & \text{可以得到}n-r\text{个线性无关的解向量：}\\ & {\boxed{\eta }}_1=\left[\begin{array}{c}-{\overline{a}}_{1(r+1)}\\ -{\overline{a}}_{2(r+1)}\\ ⋮\\ -{\overline{a}}_{r(r+1)}\\ 1\\ 0\\ ⋮\\ 0\end{array}\right],{\boxed{\eta }}_2=\left[\begin{array}{c}-{\overline{a}}_{1(r+2)}\\ -{\overline{a}}_{2(r+2)}\\ ⋮\\ -{\overline{a}}_{r(r+2)}\\ 0\\ 1\\ ⋮\\ 0\end{array}\right],\cdots ,{\boxed{\eta }}_{n-r}=\left[\begin{array}{c}-{\overline{a}}_{1n}\\ -{\overline{a}}_{2n}\\ ⋮\\ -{\overline{a}}_{rn}\\ 0\\ 0\\ ⋮\\ 1\end{array}\right]\\ & \text{它们就是齐次线性方程组}A\boxed{x}=\boxed{0}\text{的基础解系。}\end{array}$$

非齐次线性方程组解的结构

解的性质

$$\begin{array}{rl}& \text{定理：（1）如果}{\boxed{\eta }}_1,{\boxed{\eta }}_2\text{为非齐次线性方程组}A\boxed{x}=\boxed{b}\text{的两个解，则}{\boxed{\eta }}_1-{\boxed{\eta }}_2\text{为}A\boxed{x}=\boxed{0}\text{的}\\ & \text{解。}\\ & \text{（2）如果}{\boxed{\eta }}_1\text{为非齐次线性方程组}A\boxed{x}=\boxed{b}\text{的解，}{\boxed{\eta }}_2\text{为齐次线性方程组}A\boxed{x}=\boxed{0}\text{的解，}\\ & \text{则}{\boxed{\eta }}_1+{\boxed{\eta }}_2\text{为非齐次线性方程组}A\boxed{x}=\boxed{b}\text{的解。}\end{array}$$

通解

$$\begin{array}{rl}& \text{定理：设}{\boxed{\eta }}_1,{\boxed{\eta }}_2,\dots ,{\boxed{\eta }}_{n-r}\text{为齐次线性方程组}A\boxed{x}=\boxed{0}\text{的基础解系，}{\boxed{\eta }}_0\text{为非齐次线性方程组}\\ & A\boxed{x}=\boxed{b}\text{任意一个解，则非齐次线性方程组}A\boxed{x}=\boxed{b}\text{的通解可以表示为}\\ & k_1{\boxed{\eta }}_1+k_2{\boxed{\eta }}_2+\cdots +k_{n-r}{\boxed{\eta }}_{n-r}+{\boxed{\eta }}_0(k_1,k_2,\dots ,k_{n-r}\in R)。\\ & \text{【注】（1）非齐次线性方程组的通解为其导出组的通解加上它任意一个特解；}\\ & \text{（2）由定理可知求非齐次线性方程组通解的关键也是求其对应齐次线性方程的基础解系。}\end{array}$$