多项式矩阵及其史密斯smith标准型
多项式矩阵
定义
多项式矩阵也称为 λ \lambda λ-矩阵,就是将矩阵中的元素换乘由 λ \lambda λ组成的多项式
多项式矩阵的秩
K阶子式:在一个矩阵中任选K行、K列计算其行列式即为K阶子式
类似数字矩阵,多项式矩阵
A
(
λ
)
∈
K
[
λ
]
m
×
n
A(\lambda) \in \mathbb{K}[\lambda]^{m \times n}
A(λ)∈K[λ]m×n的秩定义为
r
r
r
其中要求:
- 存在 r r r阶子式是非零多项式
- 所有 r + 1 r+1 r+1阶多项式是零多项式
满秩:
n
×
n
n \times n
n×n方阵
A
(
λ
)
A(\lambda)
A(λ)的秩等于
n
n
n,则称其为满秩。
满秩的充要条件是
d
e
t
A
(
λ
)
detA(\lambda)
detA(λ)是一个非零多项式。
A
(
λ
)
A(\lambda)
A(λ)也被称为非奇异矩阵
多项式矩阵的可逆矩阵(单模矩阵)
如果 ∃ \exists ∃多项式矩阵 B ( λ ) B(\lambda) B(λ), s t . A ( λ ) B ( λ ) = B ( λ ) A ( λ ) = E st.A(\lambda)B(\lambda)=B(\lambda)A(\lambda)=E st.A(λ)B(λ)=B(λ)A(λ)=E,则称 A ( λ ) A(\lambda) A(λ)是可逆的,或者称为单模的
A ( λ ) 、 B ( λ ) A(\lambda)、B(\lambda) A(λ)、B(λ)互称逆矩阵。
这里要求 B B B矩阵必须也是多项式矩阵
可逆的充要条件:
A
(
λ
)
A(\lambda)
A(λ)可逆的充要条件是
d
e
t
A
(
λ
)
detA(\lambda)
detA(λ)是一个非零常数
同时
A
−
1
(
λ
)
=
a
d
j
A
(
λ
)
d
e
t
A
(
λ
)
A^{-1}(\lambda)=\frac{adjA(\lambda)}{detA(\lambda)}
A−1(λ)=detA(λ)adjA(λ)
其中
a
d
j
A
(
λ
)
adjA(\lambda)
adjA(λ)是伴随矩阵。
于是有一个比较明显的推论,多项式矩阵可逆,则一定是满秩的,但多项式矩阵是满秩的,则不一定可逆。
伴随矩阵对于 n n n阶矩阵 A ( λ ) A(\lambda) A(λ)其伴随矩阵 a d j A ( λ ) adjA(\lambda) adjA(λ)是由 A ( λ ) A(\lambda) A(λ)的各个元素的代数余子式构成的矩阵的转置
代数余子式:对于矩阵中的每一个元素 a i j ( λ ) a_{ij}(\lambda) aij(λ),花去它所在的第i行和第j列,剩下的称为余子式 M i j M_{ij} Mij。代数余子式 A i j = ( − 1 ) i + j M i j A_{ij}=(-1)^{i+j}M_{ij} Aij=(−1)i+jMij
将这些 A i j A_{ij} Aij排成一个矩阵
将上面有代数余子式排成的矩阵转置即得到了伴随矩阵。
多项式矩阵的初等变换
勾起了大一时远古的记忆
第一种互换变换:
互换矩阵的第
i
i
i行(或列)与第
j
j
j行(或列)
r
i
↔
r
j
r_i \leftrightarrow r_j
ri↔rj或者
c
i
↔
c
j
c_i \leftrightarrow c_j
ci↔cj
第二种倍乘变换:
用一个非零常数k乘以矩阵的第
i
i
i行(或列)
k
⋅
r
i
k \cdot r_i
k⋅ri或者
k
⋅
c
i
k \cdot c_i
k⋅ci,其中
k
∈
F
,
k
≠
0
k \in \mathbb{F}, k \neq 0
k∈F,k=0
第三种倍价变换:
将矩阵第
j
j
j行(或列)的
φ
(
λ
)
\varphi(\lambda)
φ(λ)倍加到第
i
i
i行(或列)上
r
i
+
φ
(
λ
)
r
j
r_i+\varphi(\lambda)r_j
ri+φ(λ)rj或者
c
i
+
φ
(
λ
)
c
j
c_i+\varphi(\lambda)c_j
ci+φ(λ)cj
smith标准型
矩阵等价
如果矩阵
A
(
λ
)
A(\lambda)
A(λ)可以通过有限次初等变换变成矩阵
B
(
λ
)
B(\lambda)
B(λ),那么这两个矩阵就是等价的,记作
A
(
λ
)
≅
b
(
λ
)
A(\lambda) \cong b(\lambda)
A(λ)≅b(λ).
数学表达如下:
P
(
λ
)
A
(
λ
)
Q
(
λ
)
=
B
(
λ
)
P(\lambda)A(\lambda)Q(\lambda) =B(\lambda)
P(λ)A(λ)Q(λ)=B(λ)
其中
P
(
λ
)
、
Q
(
λ
)
P(\lambda)、Q(\lambda)
P(λ)、Q(λ)事可逆方阵。
对于等价的矩阵具有相同的秩rank
A
(
λ
)
≅
B
(
λ
)
↔
r
a
n
k
A
(
λ
)
=
r
a
n
k
B
(
λ
)
A(\lambda) \cong B(\lambda) \leftrightarrow rankA(\lambda)=rankB(\lambda)
A(λ)≅B(λ)↔rankA(λ)=rankB(λ)
对于 ≅ \cong ≅是一种等价关系具有自反性、对称性、传递性
smith标准型定义
smith标准型即为 n × n n \times n n×n方阵的一种等价标准型
对于任意一个
n
×
n
n \times n
n×n的多项式矩阵
A
(
λ
)
A(\lambda)
A(λ),它都可以通过有限次初等变换简化成一个干净的对角矩阵这个对角矩阵就叫smith标准型,通常记为
S
(
λ
)
S(\lambda)
S(λ)
形式如下:
S
(
λ
)
=
(
d
1
(
λ
)
0
⋯
0
0
0
d
2
(
λ
)
⋯
0
0
⋮
⋮
⋱
⋮
⋮
0
0
⋯
d
r
(
λ
)
0
0
0
⋯
0
0
)
S(\lambda)=\begin{pmatrix}d_1(\lambda) & 0 & \cdots &0&0 \\ 0 & d_2(\lambda) & \cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & d_r(\lambda) & 0 \\ 0 & 0 & \cdots & 0 & 0\end{pmatrix}
S(λ)=
d1(λ)0⋮000d2(λ)⋮00⋯⋯⋱⋯⋯00⋮dr(λ)000⋮00
并不是所有的对角矩阵都是smith标准型,需要满足下面三个条件:
- 对角化:非对角线上的元素全为0
- 整除性:对角线上的多项式,前一个必须能整除后一个即 d i ( λ ) ∣ d i + 1 ( λ ) d_i(\lambda) | d_{i+1}(\lambda) di(λ)∣di+1(λ)
- 首一性:为了保证唯一性,规定所有
d
i
(
λ
)
d_i(\lambda)
di(λ)的最高次系数必须为1,即为
首一多项式
举个栗子🌰:
[
1
0
0
0
λ
0
0
0
λ
(
λ
+
1
)
]
\begin{bmatrix}1 & 0 & 0 \\0& \lambda &0 \\ 0 & 0 &\lambda (\lambda +1) \end{bmatrix}
1000λ000λ(λ+1)
[ λ − 1 0 0 0 λ 2 ( λ − 1 ) 0 0 0 0 ] \begin{bmatrix}\lambda-1 & 0 & 0 \\0& \lambda^2(\lambda-1) &0 \\ 0 & 0 &0 \end{bmatrix} λ−1000λ2(λ−1)0000
上面两个多项式矩阵均为smith标准型
而下面的多项式矩阵则不是smith标准型
[
1
0
0
0
λ
−
1
0
0
0
λ
(
λ
+
1
)
]
\begin{bmatrix}1 & 0 & 0 \\0& \lambda-1 &0 \\ 0 & 0 &\lambda (\lambda +1) \end{bmatrix}
1000λ−1000λ(λ+1)
[
1
0
0
0
2
λ
0
0
0
λ
(
λ
+
1
)
]
\begin{bmatrix}1 & 0 & 0 \\0& 2\lambda &0 \\ 0 & 0 &\lambda (\lambda +1) \end{bmatrix}
10002λ000λ(λ+1)
对于满秩矩阵的smith标准型为、
S
(
λ
)
=
(
d
1
(
λ
)
0
⋯
0
0
d
2
(
λ
)
⋯
0
⋮
⋮
⋱
⋮
0
0
⋯
d
r
(
λ
)
)
S(\lambda)=\begin{pmatrix}d_1(\lambda) & 0 & \cdots &0 \\ 0 & d_2(\lambda) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & d_r(\lambda) \end{pmatrix}
S(λ)=
d1(λ)0⋮00d2(λ)⋮0⋯⋯⋱⋯00⋮dr(λ)
栗子🌰求smith标准型
🌰一:求
A
(
λ
)
=
[
1
−
λ
λ
2
λ
λ
λ
−
λ
λ
−
1
−
λ
2
−
λ
]
A(\lambda)=\begin{bmatrix}1-\lambda & \lambda^2 & \lambda \\ \lambda & \lambda & -\lambda \\ \lambda - 1 & -\lambda^2 & -\lambda \end{bmatrix}
A(λ)=
1−λλλ−1λ2λ−λ2λ−λ−λ
的smith标准型
S
(
λ
)
S(\lambda)
S(λ)
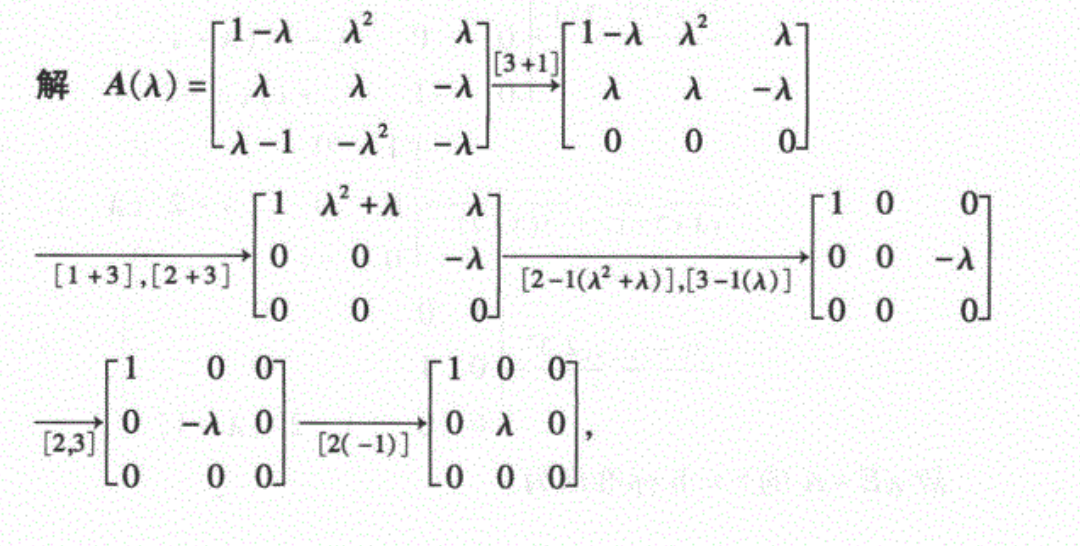
🌰二:



























 2025
2025

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








