并行计算 PCAM方法学

零、what

PCMA方法学是指划分（partitioning）、通讯（Communication）、组合（Agglomeration）、映射（Mapping）

一、 划分

1、 划分方法描述

• 划分一般先进行数据划分（域分解，domain decomposition），再进行功能分解（functional decomposition）
• 划分阶段忽略目标机器的处理器核心数和体系结构

2、 域分解

域分解划分的对象是数据，将数据划分成大致相等的小数据片（划分时考虑数据上的相应操作，如果一个任务需要别的任务的数据，则会产生任务间的通信）

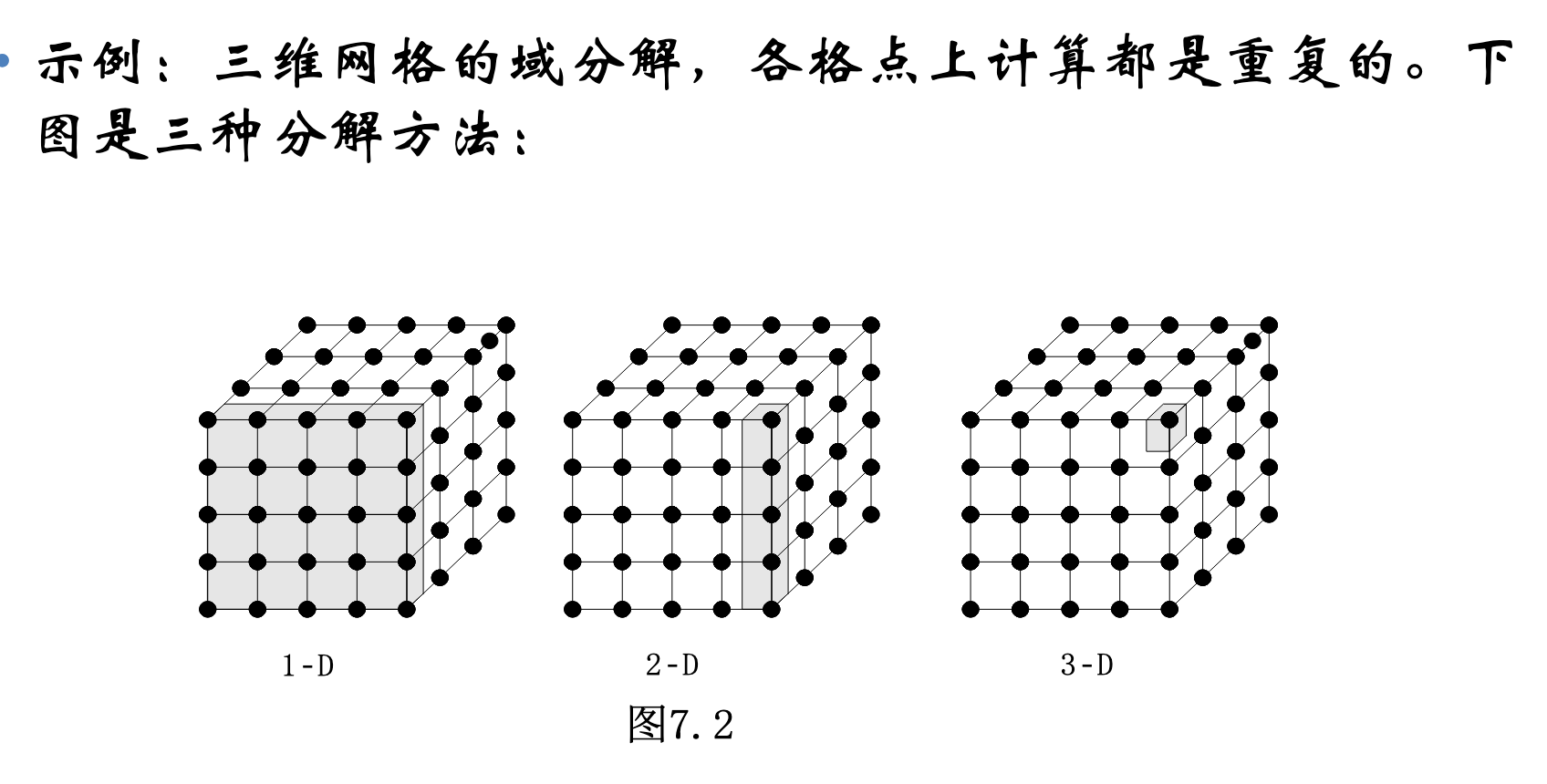
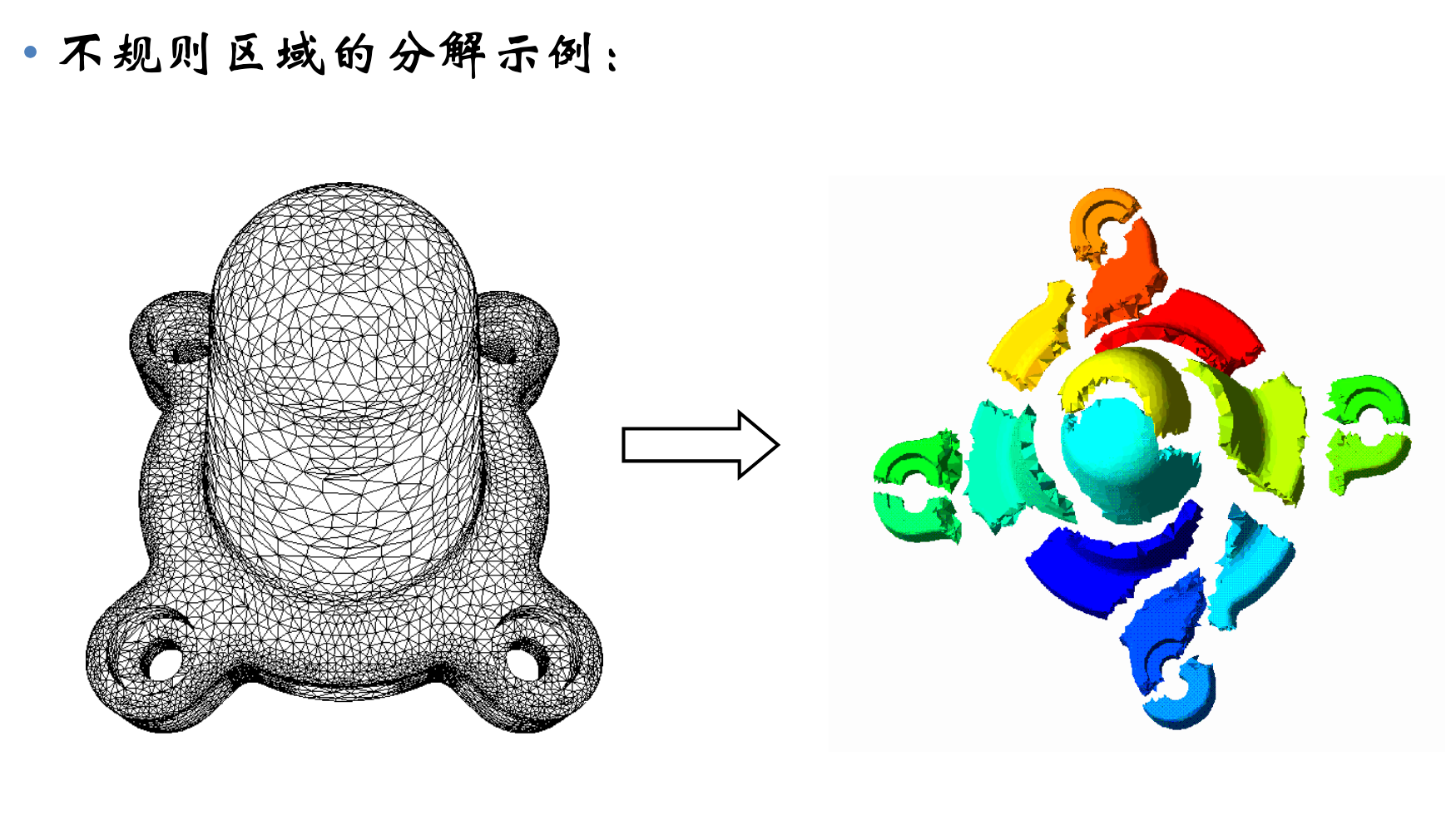
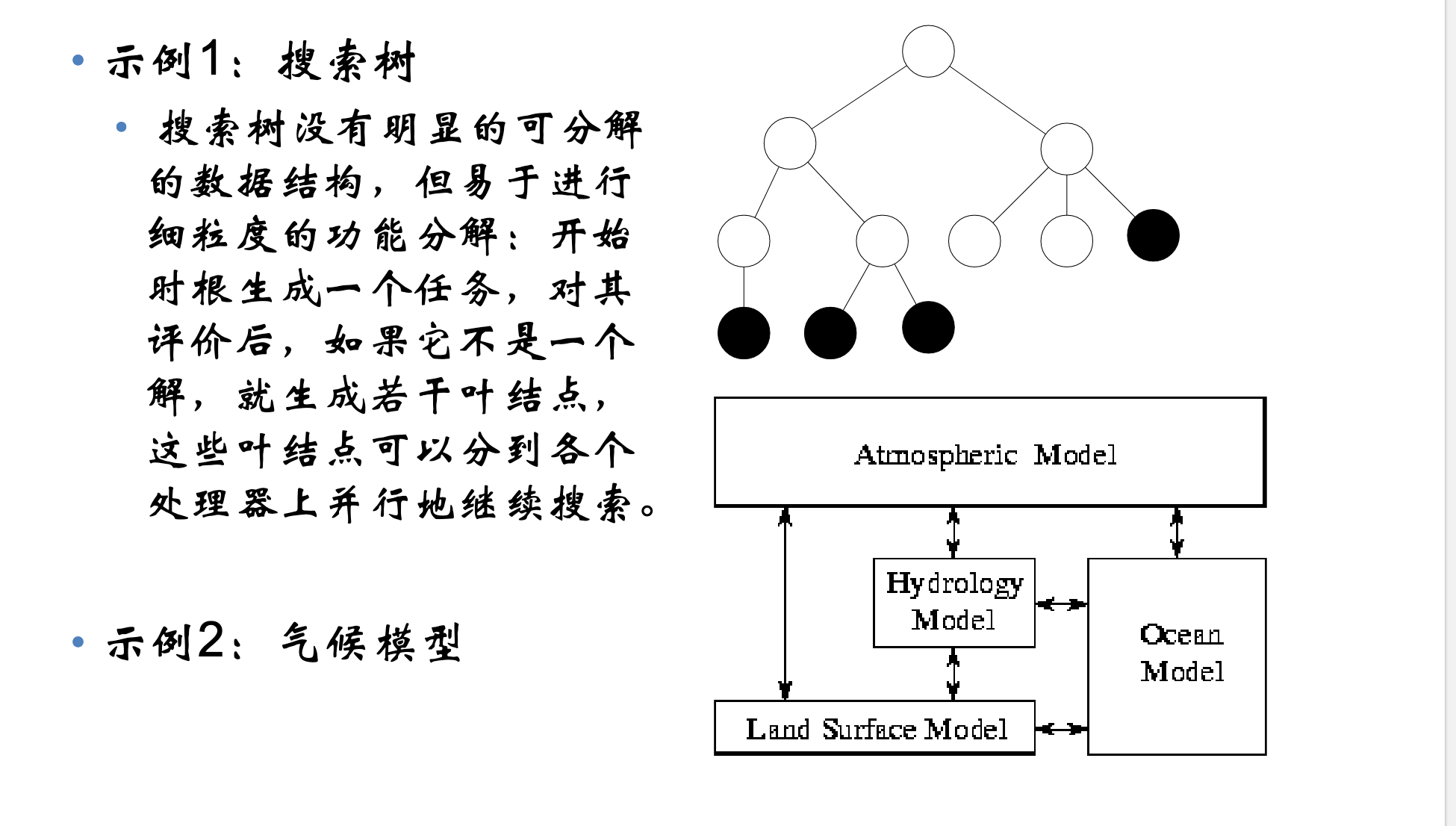
3、 功能分解

功能分解的对象是计算。
划分后,研究不同任务所需的数据。

• 如果这些数据不相交,则划分成功;
• 如果数据有相当的重叠, 意味着要重新进行域分解和功能分解;
  

4、 划分判据

1. 是否具有灵活性?
2. 是否避免了冗余计算和存储?
3. 任务尺寸是否大致相当?
4. 任务数与问题尺寸是否成比例?
5. 功能分解是一种更深层次的分解,是否合理?

二、 通信

1、 方法描述

划分产生的任务,一般不能完全独立执行,需要在任务 间进行数据交流;从而产生了通讯;
功能分解确定了诸任务之间的数据流;
各任务是并发执行的,通讯则限制了这种并发性

2、 四种通讯模式

局部｜全局通信模式
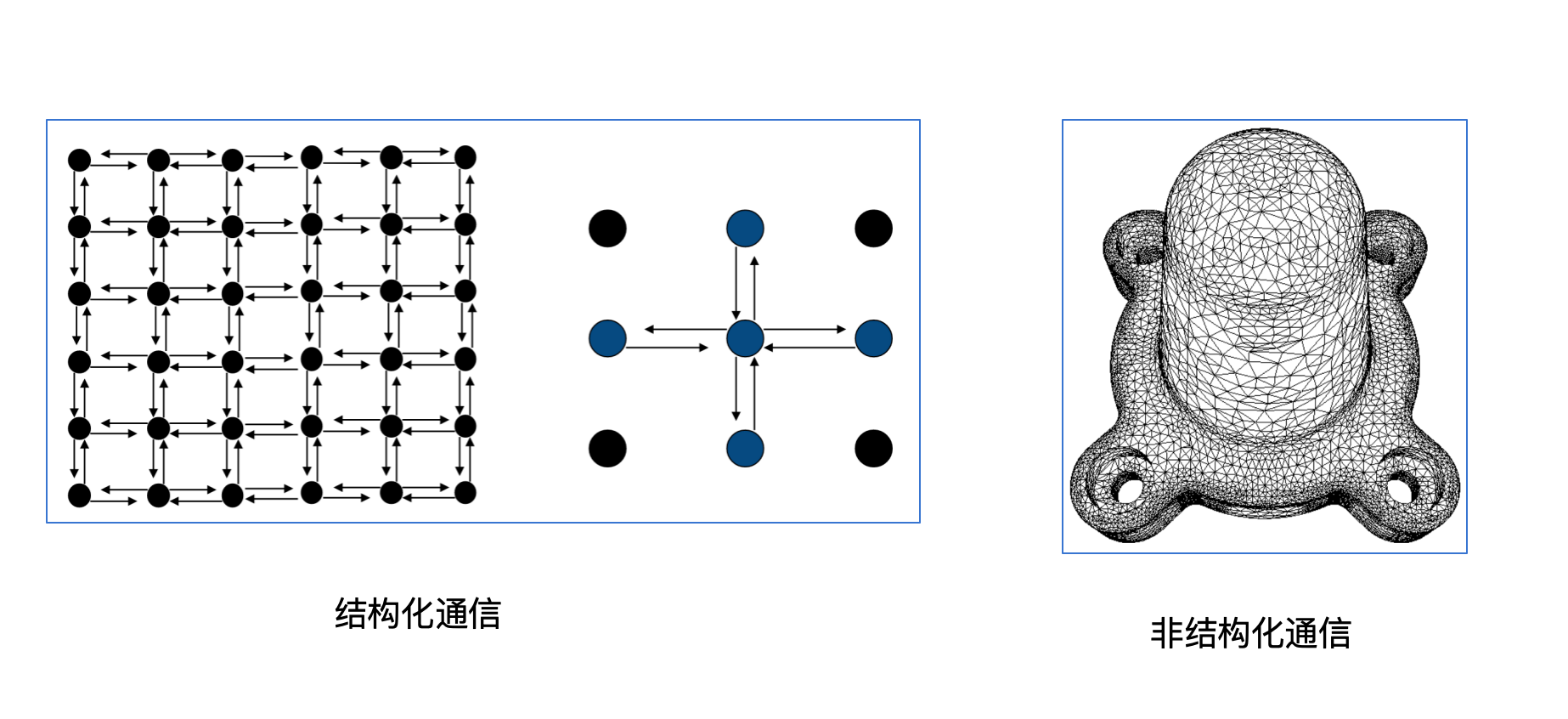
结构化｜非结构化通信模式（通信方式是否一致）
静态｜动态通信模式
同步｜异步通信

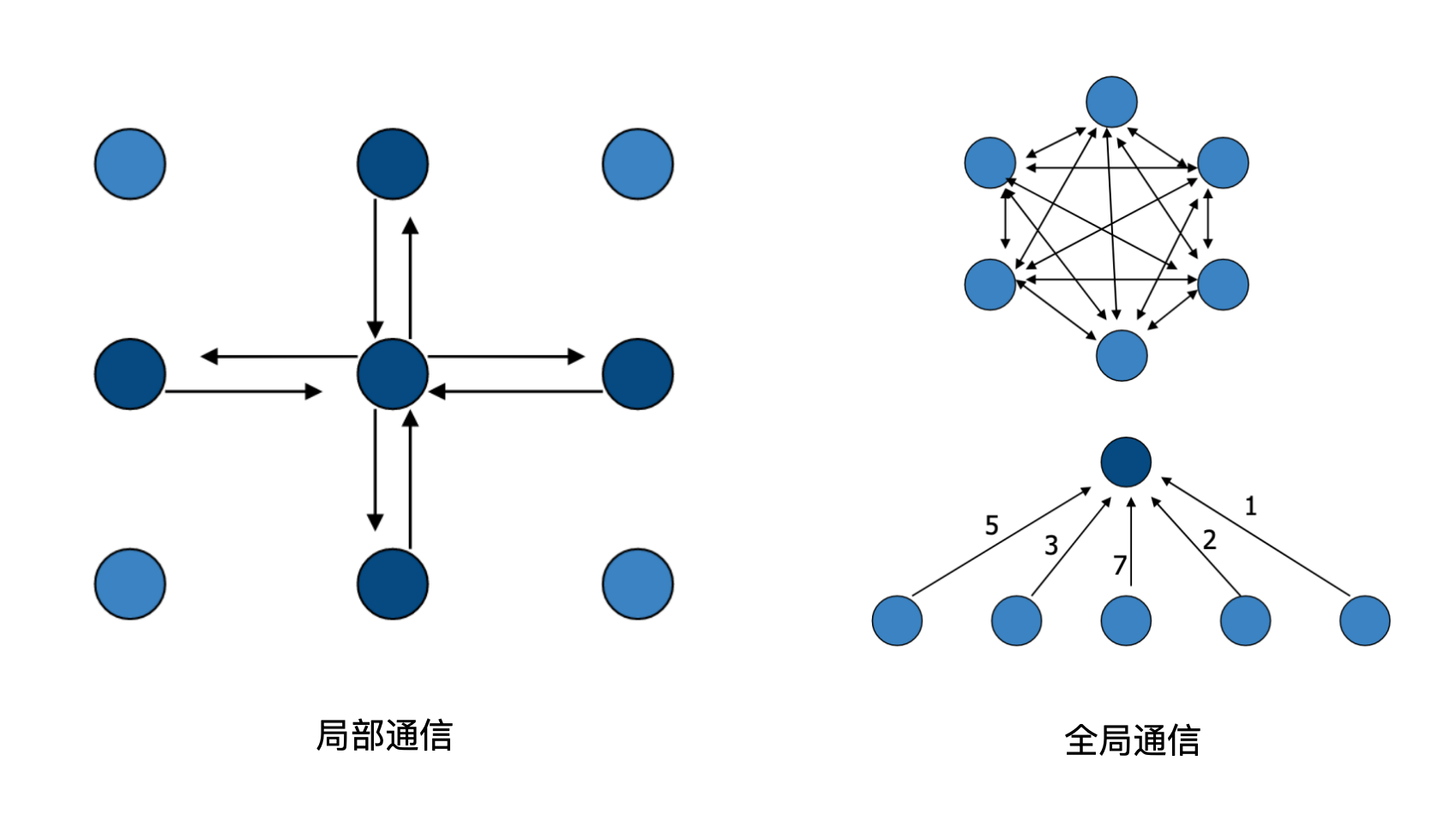
3、 通讯判据

1. 所有任务是否执行大致相当的通信
2. 是否尽可能的局部通信
3. 通信操作是否能够并行执行
4. 同步任务的计算是否能够并行执行

三、 组合

1、 方法描述

在前两个阶段（划分和通信）中，我们为了追求最大并行性，通常把任务切分得非常细（Fine-grained）。但在现实的物理机器上，管理成千上万个极小任务的开销（Overhead）是巨大的。

组合的核心目标是：在保持足够并行度的前提下，通过合并小任务来减少通信成本和管理开销。

2、 表面-容积效应

是一个几何上的概念，指随着物体尺寸，体积增长快于表面积，这里拿表面积类比通信量，容积类比计算量，随着并行任务颗粒度变大，计算量的增长是比通信量增长快，计算通信比会增加，也就是效率会增加。

3、 重复计算

4、 组合判据

1. 增加粒度是否减少了通讯成本?
2. 重复计算是否已权衡了其得益?
3. 是否保持了灵活性和可扩放性?
4. 组合的任务数是否与问题尺寸成比例?
5. 是否保持了类似的计算和通讯?
6. 有没有减少并行执行的机会?

四、 映射

1、 方法描述

每个任务要映射到具体的处理器,定位到运行机器上;

任务数大于处理器数时,存在负载平衡和任务调度问题;

映射的目标:减少算法的执行时间

并发的任务 → 不同的处理器

任务之间存在高通讯的 → 同一处理器

映射实际是一种权衡,属于NP完全问题

2、 负载平衡算法

3、 任务调度算法

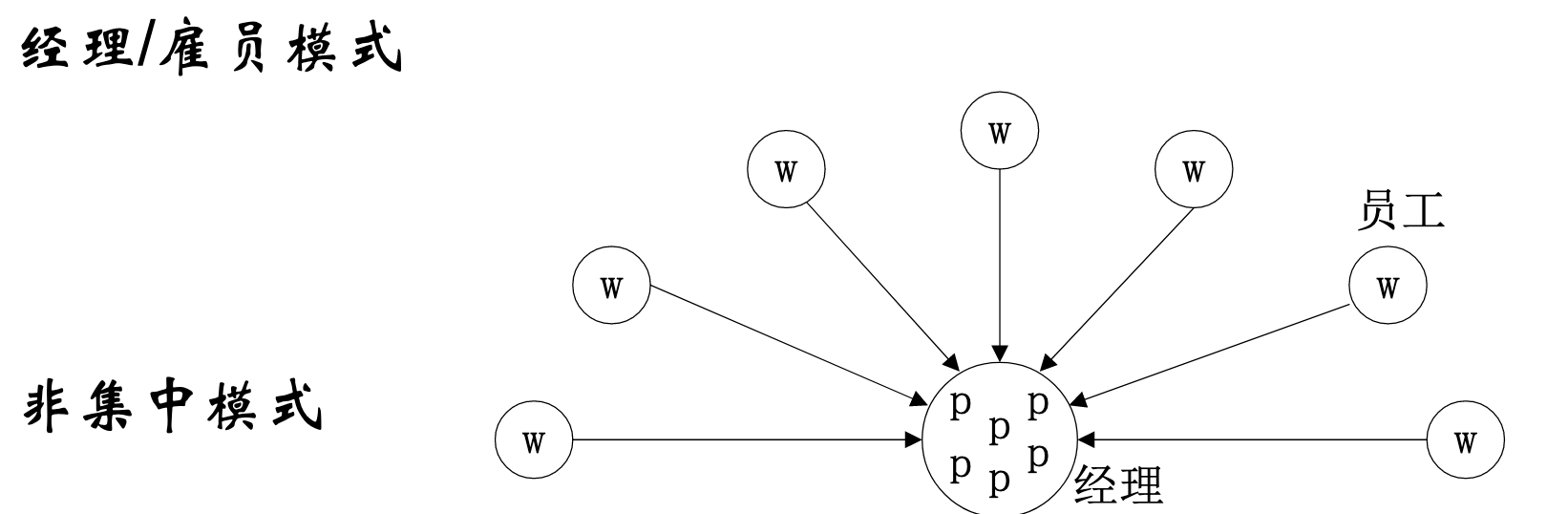
任务放在集中的或分散的任务池中,使用任务调度算法将 池中的任务分配给特定的处理器。下面是两种常用调度模式。

4、 映射判据

1. 采用集中式负载平衡方案,是否存在通讯瓶颈?

2. 采用动态负载平衡方案,调度策略的成本如何?