💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
💥1 概述
三杆桁架是一种常见的结构形式,广泛应用于桥梁、建筑物和机械设备等领域。三杆桁架的设计优化是指通过调整杆件的尺寸、形状和连接方式等参数,使得结构在满足一定约束条件下,具有最佳的性能和经济性。
本文目标函数和约束条件如下:

三杆桁架设计优化的目标主要包括以下几个方面:
1. 结构强度和刚度:三杆桁架的设计需要满足一定的强度和刚度要求,以确保结构在使用过程中不会发生失稳或破坏。优化设计可以通过调整杆件的截面积和长度等参数,使得结构在承受外载荷时具有最佳的强度和刚度。
2. 结构重量:三杆桁架的重量直接影响到结构的成本和运输安装的方便性。优化设计可以通过减少杆件的重量,使得结构在满足强度和刚度要求的前提下具有最轻的重量。
3. 结构稳定性:三杆桁架在受到外载荷作用时需要保持稳定,避免发生失稳和塑性变形。优化设计可以通过调整杆件的尺寸和形状,使得结构在承受外载荷时具有最佳的稳定性。
4. 结构的经济性:三杆桁架的设计需要考虑到材料成本、制造成本和维护成本等因素,以使得结构在满足性能要求的前提下具有最低的总成本。
为了实现三杆桁架设计的优化,研究者们采用了多种方法和技术。其中包括传统的数学优化方法,如线性规划、非线性规划和整数规划等,以及现代的优化算法,如遗传算法、粒子群算法和模拟退火算法等。这些方法和技术可以帮助研究者在设计过程中快速搜索最优解,提高设计效率。
此外,研究者们还通过建立数值模型和进行仿真分析,对三杆桁架的性能进行评估和优化。这些模型和分析方法可以帮助研究者更好地理解结构的行为和响应,指导优化设计的过程。
一、三杆桁架的基本结构与工程背景
三杆桁架是一种经典的工程结构,由三根杆件通过铰链连接形成三角形框架,具有结构简单、受力明确的特点。
- 基本组成:
- 通常包含三根杆件(标记为 b1,b2,b3),连接两个或三个节点(如节点1、2、3)。
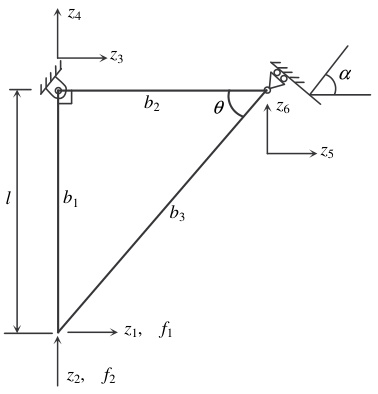
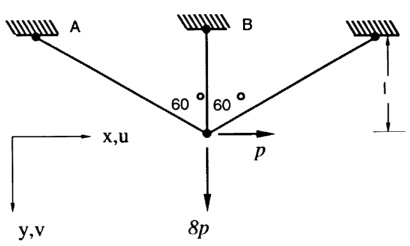
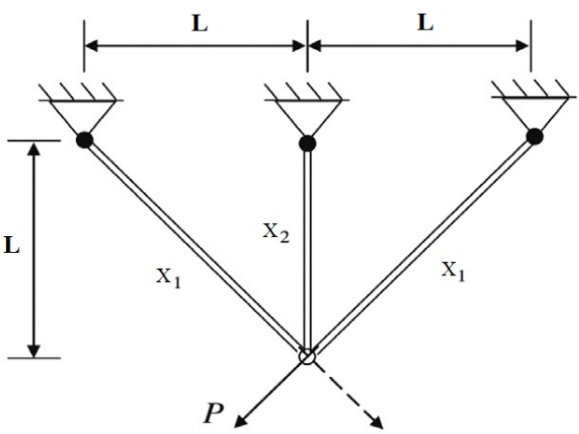
- 节点1和3固定于水平面,节点2承受外部载荷(如垂直力 PP 或复合力 Fx,FyFx,Fy)。
- 常见构型包括等边三角形(杆长均为 LL)或非对称布局。
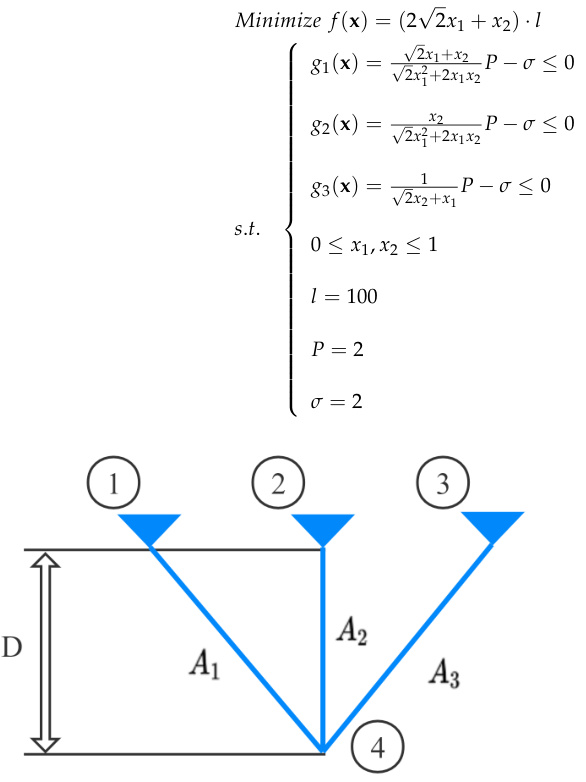
- 通常包含三根杆件(标记为 b1,b2,b3),连接两个或三个节点(如节点1、2、3)。
- 应用场景:
- 桥梁支撑、建筑屋顶、机械装备中承受复杂载荷的结构。
- 普拉特桁架(斜杆向内)适用于中等跨度,豪威桁架(斜杆向外)适用于大跨度。
设计意义:三杆桁架是结构优化领域的基准模型,因其超静定特性和明确的力学响应,常用于验证优化算法的有效性。
二、优化目标与设计准则
优化目标需在满足安全约束下提升性能与经济性,主要包括:
- 重量最小化:
- 核心目标,直接降低材料成本与运输安装难度。
- 例如:ANSYS优化案例将初始重量109.10磅减少11%,目标函数为 minW=ρ∑AiLi(Ai为截面积,Li为杆长)。
- 刚度最大化:
- 通过最小化结构柔度(compliance)实现,即 minc=∑wlUlTFlminc=∑wlUlTFl(UlUl为位移向量,FlFl为载荷向量)。
- 稳定性与强度:
- 避免失稳和塑性变形,约束杆件应力 σi≤[σ]σi≤[σ] 及节点位移 uj≤[u]uj≤[u]。
- 成本控制:
- 结合材料单价与制造工艺,多目标优化中考虑重量、成本、位移的权衡。
矛盾与平衡:轻量化可能削弱刚度,需通过多目标优化或约束协调(如应力限值400MPa)。
三、数学建模与优化方法
1. 有限元分析(FEA)
- 流程:
- 建立几何模型 → 定义材料属性(E,ρ,ν)→ 划分网格 → 施加载荷与约束 → 求解应力/位移 → 迭代优化。
- ANSYS案例:
- 设计变量:杆件截面积 A1,A2,A3 和跨度 BB(范围 Ai∈[1,1000] in2], B∈[400,1000] in。
- 状态变量:杆件应力 σi≤400 psi,目标函数:最小化质量。
2. 拓扑优化
- 类桁架连续体模型:
- 将杆件密度 αbj和方向作为设计变量,通过插值实现连续变化,避免传统“有/无单元”的锯齿边界问题。
- 优点:无中间密度抑制,数值稳定性高。
- 特征线提取:
- 从拓扑结果中提取杆件轴线,便于工程制造。
3. 智能优化算法
| 算法 | 优化结果 | 优势 | 来源 |
|---|---|---|---|
| CPOEBWO | 最小体积263.24 cm³ (A1=0.7898 cm2,A2=0.3985 cm2) | 全局寻优能力强 | |
| 遗传算法(GA) | 离散变量优化,优于传统梯度法 | 处理离散变量,避免局部最优 | |
| 混合算法(haDEPSO) | 收敛速度快,标准差小 | 结合差分进化与粒子群优势 |
算法选择趋势:融合混沌映射(如Fuch映射)、自适应权重(如MAO算法)提升收敛精度。
四、材料选择的影响
- 各向同性 vs 各向异性材料:
- 拓扑优化本质要求各向异性(如类桁架连续体),碳纤维(CFRP)等复合材料可更好匹配理论模型。
- 热变形控制:
- 空间结构中,CFRP的低温膨胀系数(如M40碳纤维)显著降低热变形,提升尺寸稳定性。
- 成本与工艺:
- 金属基板(如钛合金)用于复杂接头,平衡机加工性能与碳纤维配合需求。
多材料优化案例:遗传算法同时优化杆件材料与截面积,实现重量-成本-位移的帕累托前沿。
五、约束条件与工程可行性
约束是保证结构安全的核心,主要包括:
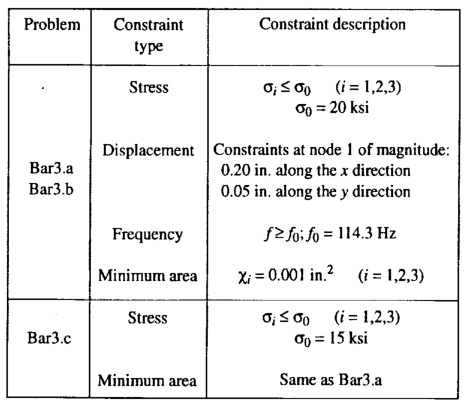
- 应力约束:
- 位移约束:
- 节点位移限值(如合位移 ≤5 mm≤5mm)。
- 几何与稳定性约束:
- 避免零杆删除导致机构失稳,需合并共线杆件。
- 基频约束(如 f≥114.3 Hzf≥114.3Hz)防止共振。
六、典型案例研究

- 类桁架连续体柔度优化:
- 方法:优化杆件分布场,生成非正交杆系结构(图1d)。
- 优势:捕捉传统方法无法实现的细节特征。
七、未来研究方向
- 多物理场耦合:热-力联合优化(如空间望远镜桁架)。
- 智能算法深化:自适应参数调整、多目标帕累托前沿精细化。
- 制造约束集成:将加工工艺(如焊接成本)纳入优化模型。
结论:三杆桁架优化需综合结构力学、材料科学和算法设计,其研究成果可推广至复杂桁架系统,推动工程结构的高效安全设计。
📚2 运行结果

部分代码:
function [lb,ub,dim,fobj] = Engineering_Problems(type)
% type:问题类型
% 不同数字 对应 不同问题
% 比如,type = 1 : 选择优化 Tension/compression spring design problem
% type = 2 : 选择优化 Pressure vessel design problem
switch type
case 1 % Tension/compression spring design problem
fobj = @spring; % 函数
lb = [0.05 0.25 2]; % 下限
ub = [2 1.3 15]; % 上限
dim = length(lb); % 维度
case 2 % Pressure vessel design problem
fobj = @ pvd;
lb =[0 0 10 10];
ub = [99 99 200 200];
dim = length(lb);
case 3 % Three-bar truss design problem
fobj = @ three_bar;
lb = [0 0];
ub = [1 1];
dim = length(lb);
end
function fitness = spring(x)
x1 = x(1);
x2 = x(2);
x3 = x(3);
f = (x3+2)*x2*(x1^2);
panaty_factor = 10e100; % 按需修改
%
g1 = 1-((x2^3)*x3)/(71785*(x1^4));
g2 = (4*(x2^2)-x1*x2)/(12566*(x2*(x1^3)-(x1^4))) + 1/(5108*(x1^2))-1;
g3 = 1-(140.45*x1)/((x2^2)*x3);
g4 = ((x1+x2)/1.5)-1;
panaty_1 = panaty_factor*(max(0,g1))^2; % g1的惩罚项
panaty_2 = panaty_factor*(max(0,g2))^2; % g2的惩罚项
panaty_3 = panaty_factor*(max(0,g3))^2; % g3的惩罚项
panaty_4 = panaty_factor*(max(0,g4))^2; % g4的惩罚项
fitness = f + panaty_1+panaty_2+panaty_3+panaty_4;
end
function fitness = pvd(x)
x1= x(1);x2 = x(2);x3 = x(3);x4 = x(4);
f = 0.6224*x1*x3*x4 + 1.7781*x2*x3^2+3.1661*x1^2*x4+19.84*x1^2*x3;
panaty_factor = 10e100; % 按需修改
%
g1 = -x1+0.0193*x3;
panalty_1 = panaty_factor*(max(0,g1))^2;
g2 = -x2+0.00954*x3;
panalty_2 = panaty_factor*(max(0,g2))^2;
g3 = -pi*x3^2*x4 - (4/3)*pi*x3^3 + 1296000;
panalty_3 = panaty_factor*(max(0,g3))^2;
g4 = x4 - 240;
panalty_4 = panaty_factor*(max(0,g4))^2;
fitness = f + panalty_1 + panalty_2 + panalty_3 + panalty_4;
end
function fitness = three_bar(x)
l = 100; P = 2; q = 2;
x1= x(1);
x2 = x(2);
f = l*(2*sqrt(2)*x1+x2);
panaty_factor = 10e100; % 按需修改
%
g1 = P*(sqrt(2)*x1+x2)/(sqrt(2)*x1^2+2*x1*x2)-q;
penalty_g1 = panaty_factor*(max(0,g1))^2;
g2 = P*(x2)/(sqrt(2)*x1^2+2*x1*x2)-q;
penalty_g2 = panaty_factor*(max(0,g2))^2;
g3 = P/(sqrt(2)*x2+x1)-q;
penalty_g3 = panaty_factor*(max(0,g3))^2;
fitness = f+penalty_g1+penalty_g2+penalty_g3;
end
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]叶友东,王雅.基于ANSYS分析的三杆桁架优化设计[J].煤矿机电, 2004(5):5.DOI:10.3969/j.issn.1001-0874.2004.05.039.
[2]朱钦,杨海霞.基于粒子群-布谷鸟搜索算法的桁架结构优化设计[J].三峡大学学报(自然科学版), 2017(1).DOI:10.13393/j.cnki.issn.1672-948X.2017.01.014.





















 1033
1033

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










