MATLAB中B样条曲线曲面拟合的实现

最新推荐文章于 2025-11-23 20:38:09 发布

原创最新推荐文章于 2025-11-23 20:38:09 发布 · 361 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

一、B样条拟合基础理论

数学模型

B样条曲线由控制点Pi和节点向量 $U = [u 0, u 1, ..., u m + k + 1]$ 定义，其参数方程为：

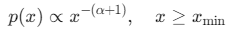
其中 $N i, k (u)$ 为 $k$ 阶 $B$ 样条基函数，满足局部支撑性和非负性。
关键参数选择 阶数(k)：三次B样条（k=3）在工程中应用最广，平衡了平滑性与灵活性。 节点向量：均匀节点适合简单形状，非均匀节点（如Chordal分布）可适应复杂数据分布。 控制点密度：通常建议控制点数=数据点数×0.3~0.5以保持拟合精度。

二、MATLAB实现流程

1. 曲线拟合

% 示例：三次B样条曲线拟合散点数据
clc; clear; close all;

% 输入数据点（x,y坐标）
data = load('sample_data.txt'); % 假设数据为N×2矩阵
x_data = data(:,1); y_data = data(:,2);

% 参数化（Chordal长度法）
n = size(data,1);
u = zeros(n,1);
for i=2:n
    u(i) = u(i-1) + norm(data(i,:) - data(i-1));
end
u = [0; u(2:end)] / u(end); % 归一化到[0,1]

% 构建B样条基函数
k = 3; % 三次B样条
t = augknt(u, k); % 增强节点向量
sp = spapi(t, data'); % 生成样条结构

% 曲线计算与绘图
u_eval = linspace(0,1,1000);
curve = fnval(sp, u_eval);
figure;
plot(data(:,1), data(:,2), 'bo', 'MarkerFaceColor','b'); hold on;
plot(curve(1,:), curve(2,:), 'r-', 'LineWidth',2);
legend('原始数据', 'B样条拟合曲线'); grid on;

2. 曲面拟合

% 示例：非均匀B样条曲面拟合三维点云
% 输入数据点（X,Y,Z）
[X,Y,Z] = load('mesh_data.mat'); % 假设为结构体数组

% 控制点网格构造
ctrlPts = reshape([X(:), Y(:), Z(:)], [], 3); % 转换为Nx3矩阵
[m,n] = size(ctrlPts)/3; % 控制点维度

% 节点向量定义（非均匀）
knots_u = [0 0 0 0 1 1 1 1]; % u方向节点
knots_v = [0 0 0 0 1 1 1 1]; % v方向节点

% 生成B样条曲面
sp_u = spapi(knots_u, ctrlPts(:,1));
sp_v = spapi(knots_v, ctrlPts(:,2));
sp_z = spapi(knots_u, ctrlPts(:,3));

% 参数采样与曲面计算
[u,v] = ndgrid(linspace(0,1,50));
X_fit = fnval(sp_u, u);
Y_fit = fnval(sp_v, v);
Z_fit = fnval(sp_z, u);

% 可视化
figure;
surf(X_fit, Y_fit, Z_fit, 'EdgeColor','none', 'FaceLighting','phong');
hold on; plot3(ctrlPts(:,1), ctrlPts(:,2), ctrlPts(:,3),'ko-');
xlabel('X'); ylabel('Y'); zlabel('Z'); view(3); camlight;

三、应用场景

动态曲面变形

通过滑块控件实时调整控制点位置，实现交互式曲面编辑：

h = figure; 
s = uicontrol('Style','slider','Position',[20 20 200 20],...
    'Min',-1,'Max',1,'Value',0,'Callback',@updateCtrlPts);

function updateCtrlPts(src,event)
    delta = event.Value*0.1;
    ctrlPts(:,3) = ctrlPts(:,3) + delta;
    % 重新计算曲面并刷新显示
    Z_fit = fnval(sp_z, u);
    surf(X_fit, Y_fit, Z_fit); 
end

多尺度拟合

采用小波变换对B样条系数进行多分辨率分析，实现粗-细两级拟合：

[c,l] = wavedec2(ctrlPts,3,'db4'); % 3层小波分解
cA = appcoef2(c,l,'db4',1); % 低频系数
cD = detcoef2('all',c,l); % 高频细节
% 仅保留低频分量进行平滑拟合
c_fit = waverec2([cA; zeros(size(cD))],l,'db4');