理论基础 —— 排序 —— 原始冒泡排序

最新推荐文章于 2023-11-23 02:00:40 发布

原创最新推荐文章于 2023-11-23 02:00:40 发布 · 862 阅读

1 ·

CC 4.0 BY-SA版权

理论基础——排序专栏收录该内容

13 篇文章

订阅专栏

本文详细介绍冒泡排序的基本原理、排序过程及其实现方法，并通过具体实例演示排序过程，同时分析了冒泡排序的时间和空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【概述】

冒泡排序是一种稳定的排序方法，也是交换排序中最简单的排序方法，其基本思想是：两两比较相邻记录的关键码，若反序则交换，直到没有反序为止。

冒泡排序的实现依靠，双重循环，外层 i 控制进行多少轮，内层循环 j 控制每轮比较的次数，对于 n 个元素，共进行 n-1 趟交换，每趟比较 n-i 次。

【排序过程】

1.排序过程

具体的排序过程为：

将整个待排序的序列分为有序区和无序区，初始时有序区为空，无序区包含所有待排序记录
对无序区从前向后依次将相邻记录的关键码进行比较，若反序则交换，从而使得关键码小的记录前移，关键码大的记录后移
重复执行步骤 2，直到无序区没有反序记录

2.实例

初始关键字：『 6，5，3，1，8，7，2，4 』

第一趟排序：『6，5，3，1，8，7，2，4 』

5，『 6，3，1，8，7，2，4 』

5，3，『 6，1，8，7，2，4 』

5，3，1，『 6，8，7，2，4 』

5，3，1，6，『 8，7，2，4 』

5，3，1，6，7，『 8，2，4 』

5，3，1，6，7，2，『 8，4 』

5，3，1，6，7，2，4，『 8 』

第二趟排序：『 5，3，1，6，7，2，4 』，8

3，『5，1，6，7，2，4』，8

3，1，『5，6，7，2，4』，8

3，1，5，『6，7，2，4』，8

3，1，5，6，『7，2，4』，8

3，1，5，6，2，『7，4』，8

3，1，5，6，2，4，『7』，8

第三趟排序：『 3，1，5，6，2，4 』，7，8

1，『3，5，6，2，4』，7，8

1，3，『5，6，2，4』，7，8

1，3，5，『6，2，4』，7，8

1，3，5，2，『6，4』，7，8

1，3，5，2，4，『6』，7，8

第四趟排序： 『 1，3，5，2，4 』，6，7，8

1，『3，5，2，4』，6，7，8

1，3，『5，2，4』，6，7，8

1，3，2，『5，4』，6，7，8

1，3，2，4，『5』，6，7，8

第五趟排序：『 1，3，2，4 』，5，6，7，8

1，『3，2，4』，5，6，7，8

1，2，『3，4』，5，6，7，8

1，2，3，『4』，5，6，7，8

第六趟排序：『 1，2，3 』，4，5，6，7，8

1，『2，3』，4，5，6，7，8

1，2，『3』，4，5，6，7，8

第七趟排序：『 1，2 』，3，4，5，6，7，8

『 1 』，2，3，4，5，6，7，8

结果： 『 1，2，3，4，5，6，7，8 』

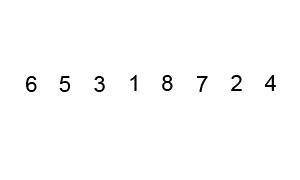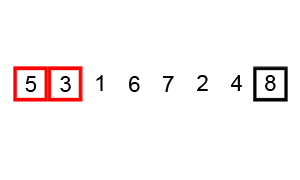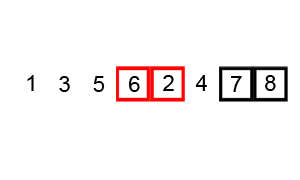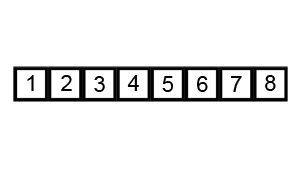
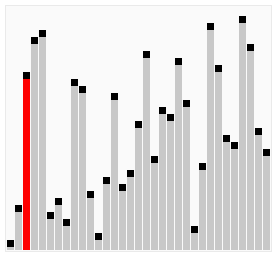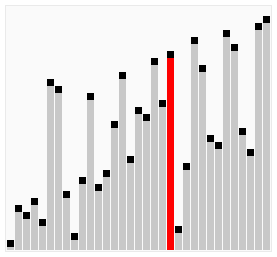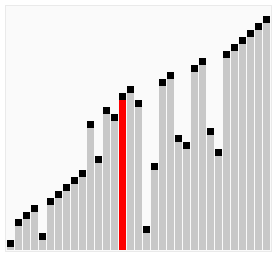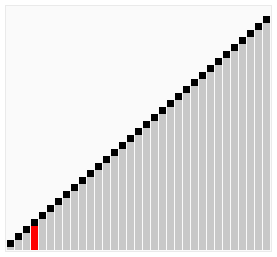
排序过程宏观过程

【时空复杂度分析】

最好的情况，是要排序的表本身就是有序的，那么在加了判断优化的实现中，只需要进行 n-1 次比较，没有数据交换，因此最优时间复杂度为 O(n)

最坏的情况，是要排序的表是逆序的情况，因此供需比较 n(n-1)/2 次，并作等数量级的记录移动，因此最坏时间复杂度为 O(n^2)

而在平均情况下，时间复杂度与最坏时间复杂度同数量级，即平均时间复杂度为 O(n^2)

此外，冒泡排序仅需一个辅助空间，用于作记录交换的暂存单元，即空间复杂度为 O(1)

【源程序】

1.朴素实现

void bubbleSort(int a[],int n){
    for(int i=1;i<=n-1;i++)//比较n-1趟
        for(int j=1;j<=n-i;j++)//每趟交换n-i次
            if(a[j]>a[j+1])
                swap(a[j],a[j+1]);
}

2.判断优化

void bubbleSort(int a[],int n){
    for(int i=1;i<=n-1;i++){//比较n-1趟
        bool flag=true;//判断是否有交换
        for(int j=1;j<=n-i;j++){//每趟交换n-i次
            if(a[j]>a[j+1]){
                swap(a[j],a[j+1]);
                flag=false;//有交换说明仍需排序
            }
        }
        if(flag)//若无交换，终止循环
            break;
    }
}